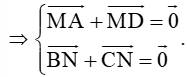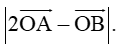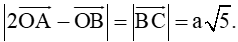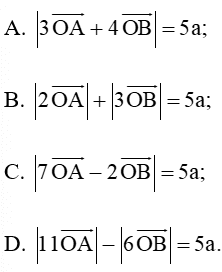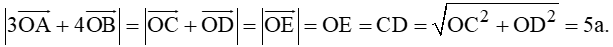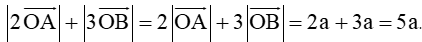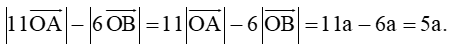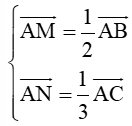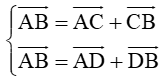50 câu Trắc nghiệm Tích của một số với một vectơ (có đáp án 2024) – Toán 10 Cánh diều
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 5: Tích của một số với một vectơ đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 5.
Trắc nghiệm Toán 10 Bài 5: Tích của một số với một vectơ
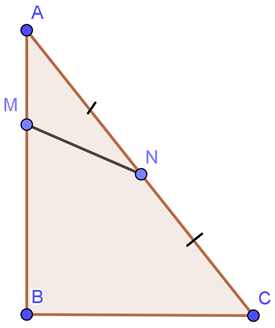
Câu 1: Cho tam giác ABC điểm M thuộc cạnh AB sao cho 3AM=AB và N là trung điểm của AC. Tính →MN theo →AB và →AC.
A. →MN=12→AC+13→AB;
B. →MN=12→AC−13→AB;
C. →MN=12→AB+13→AC;
D. →MN=12→AC−13→AB.
Đáp án đúng là: B
Vì N là trung điểm AC nên 2→MN=→MA+→MC=→MA+→MA+→AC.
⇔2→MN=2→MA+→AC
Do M là điểm thuộc cạnh AB và 3AM = AB nên →AB=3→AM=−3→MA
Do đó, 2→MN=2→MA+→AC=−23→AB+→AC
Suy ra →MN=−13→AB+12→AC.
Câu 2: Cho tam giác ABC. Hai điểm M, N chia cạnh BC theo ba phần bằng nhau BM=MN=NC. Tính →AM theo →AB và →AC.
A. →AM=23→AB+13→AC;
B. →AM=13→AB+23→AC;
C. →AM=23→AB−13→AC;
D. →AM=13→AB−23→AC.
Đáp án đúng là: A
Theo giả thiết ta có: →BM=→MN=→NC=13→BC
Ta có: →AM=→AB+→BM=→AB+13→BC=→AB+13(→AC−→AB)=23→AB+13→AC.
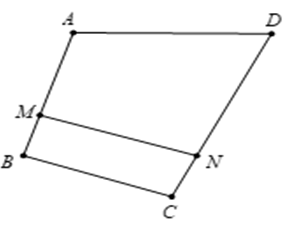
Câu 3. Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho 3→AM=2→AB và 3→DN=2→DC. Tính vectơ →MN theo hai vectơ →AD,→BC.
A. →MN=13→AD+13→BC;
B. →MN=13→AD−23→BC;
C. →MN=13→AD+23→BC;
D. →MN=23→AD+13→BC.
Đáp án đúng là: C
Ta có : →MN=→MA+→AD+→DN và →MN=→MB+→BC+→CN.
Suy ra 3→MN=→MA+→AD+→DN+2(→MB+→BC+→CN)
=(→MA+2→MB)+→AD+2→BC+(→DN+2→CN).
Theo bài ra, ta có: →MA+2→MB=→0 và →DN+2→CN=→0. Thật vậy:
3→AM=2→AB⇔3→AM=2(→AM+→MB)
⇔3→AM=2→AM+2→MB
⇔→AM=2→MB
⇔2→MB−→AM=0
⇔2→MB+→MA=0
3→DN=2→DC⇔3→DN=2(→DN+→NC)
⇔3→DN=2→DN+2→NC
⇔→DN=2→NC
⇔→DN−2→NC=0
⇔→DN+2→CN=0
Vậy 3→MN=→AD+2→BC⇔→MN=13→AD+23→BC.
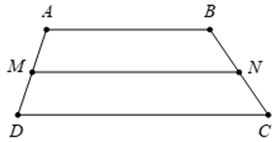
Câu 4. Cho hình thang ABCD có đáy là AB và CD. Gọi M và N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai ?
A. →MN=→MD+→CN+→DC;
B. →MN=→AB−→MD+→BN;
C. →MN=12(→AB+→DC);
D. →MN=12(→AD+→BC).
Đáp án đúng là: D
Vì M, N lần lượt là trung điểm của AD, BC
Dựa vào đáp án, ta có nhận xét sau:
- A đúng, vì →MD+→CN+→DC=(→MD+→DC)+→CN=→MC+→CN=→MN.
- B đúng, vì →AB−→MD+→BN=(→AB+→BN)−→MD=→AN−→AM=→MN.(vì M là trung điểm của AD nên →AM=→MD)
- C đúng, vì →MN=→MA+→AB+→BN và →MN=→MD+→DC+→CN.
Suy ra 2→MN=(→MA+→MD)+→AB+→DC+(→BN+→CN)=→0+→AB+→DC+→0=→AB+→DC
⇒→MN=12(→AB+→DC).
Vậy chỉ còn đáp án D.
Câu 5. Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng ?
A. →DM=12→CD+→BC;
B. →DM=12→CD−→BC;
C. →DM=12→DC−→BC;
D. →DM=12→DC+→BC.
Đáp án đúng là: C
Xét các đáp án ta thấy cần phân tích vectơ →DM theo hai vectơ →DC và →BC.
Vì ABCD là hình bình hành nên →DB=→DA+→DC.
Và M là trung điểm AB nên 2→DM=→DA+→DB
⇔2→DM=→DA+→DA+→DC
⇔2→DM=2→DA+→DC.
⇔2→DM=−2→BC+→DC suy ra →DM=12→DC−→BC.
Câu 6. Cho tam giác OAB vuông cân tại O cạnh OA = a. Tính
A. a;
B. (1+√2)a;
C. a√5;
D. 2a√2.
Đáp án đúng là: C
Gọi C là điểm đối xứng của O qua A⇒OC=2a.Tam giác OBC vuông tại O có BC=√OB2+OC2=a√5.
Ta có : 2→OA−→OB=→OC−→OB=→BC, suy ra :
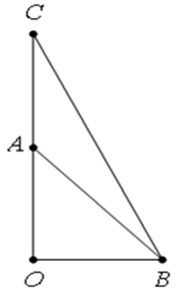
Câu 7. Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:
Đáp án đúng là: C
Dựa vào các đáp án, ta có nhận xét sau:
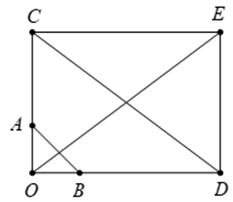
- Gọi C nằm trên tia đối của tia AO sao cho
OC=3OA⇒3→OA=→OC.
Và D nằm trên tia đối của tia BO sao cho
OD=4OB⇒4→OB=→OD.
Dựng hình chữ nhật OCED suy ra →OC+→OD=→OE (quy tắc hình bình hành).
Ta có:
Do đó, A đúng
- B đúng, vì
- D đúng, vì
Vậy chỉ còn đáp án C.
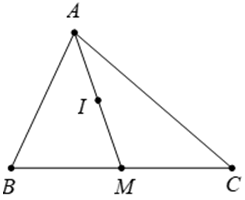
Câu 8. Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?
A. →IB+2→IC+→IA=→0;
B. →IB+→IC+2→IA=→0;
C. 2→IB+→IC+→IA=→0;
D. →IB+→IC+→IA=→0.
Đáp án đúng là: B
Vì M là trung điểm BC nên →IB+→IC=2→IM.
Mặt khác I là trung điểm AM nên →IA+→IM=→0.
Suy ra →IB+→IC+2→IA=2→IM+2→IA=2(→IM+→IA)=→0.
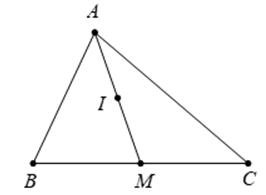
Câu 9. Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?
A. →AI=14(→AB+→AC);
B. →AI=14(→AB−→AC);
C. →AI=14→AB+12→AC;
D. →AI=14→AB−12→AC.
Đáp án đúng là: A
Vì M là trung điểm BC nên
→AB+→AC=2→AM. (1)
Mặt khác I là trung điểm AM nên
2→AI=→AM. (2)
Từ (1),(2) suy ra →AB+→AC=4→AI⇔→AI=14(→AB+→AC).
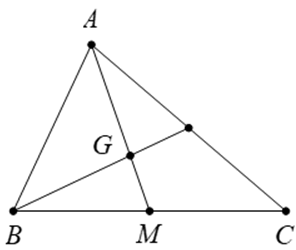
Câu 10. Cho tam giác ABC có M là trung điểm của BC, G là trọng tâm của tam giác ABC. Khẳng định nào sau đây đúng ?
A. →AG=23(→AB+→AC);
B. →AG=13(→AB+→AC);
C. →AG=13→AB+22→AC;
D. →AI=23→AB+3→AC.
Đáp án đúng là: B
Vì G là trọng tâm của tam giác ABC
⇒→AG=23→AM.
Và M là trung điểm của BC
⇒→AB+→AC=2→AM⇔→AM=12(→AB+→AC).
Do đó →AG=23.12(→AB+→AC)=13(→AB+→AC).
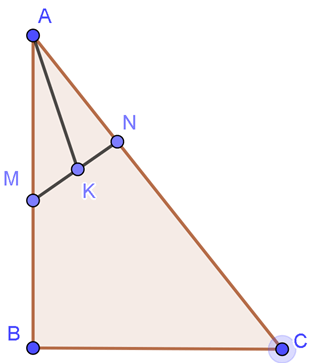
Câu 11: Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho NC=2NA. Gọi K là trung điểm của MN. Khi đó :
A. →AK=16→AB+14→AC.
B. →AK=14→AB−16→AC.
C. →AK=14→AB+16→AC.
D. →AK=16→AB−14→AC.
Đáp án đúng là: C
Vì K là trung điểm của MN nên ta có :
Ta có : →AK=12(→AM+→AN).
Mà M là trung điểm của AB và N là điểm thuộc cạnh AC sao cho NC = 2AN nên ta có :
Do đó, →AK=12(12→AB+13→AC)=14→AB+16→AC
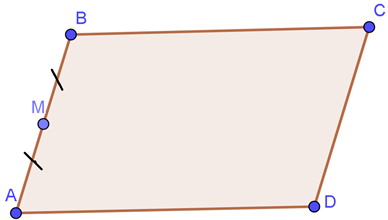
Câu 12: Cho hình bình hành ABCD. Tính →AB theo →AC và →BD.
A. →AB=12→AC+12→BD;
B. →AB=12→AC−12→BD;
C. →AB=→AM−12→BC;
D. →AB=12→AC−→BD.
Đáp án đúng là: A
Vì ABCD là hình bình hành nên →CB+→AD=→0.
Ta có :
⇒2→AB=→AC+→DB+(→CB+→AD)=→AC+→DB
⇒→AB=12→AC+12→BD.
Câu 13: Cho tam giác ABC và đặt →a=→BC,→b=→AC.> Cặp vectơ nào sau đây cùng phương?
A. 2→a+→b,→a+2→b;
B. 2→a−→b,→a−2→b;
C. 5→a+→b,−10→a−2→b;
D. →a+→b,→a−→b.
Đáp án đúng là: C
Dễ thấy −10→a−2→b=−2(5→a+→b)⇒hai vectơ 5→a+→b,−10→a−2→b cùng phương
Câu 14: Cho tam giác ABC và điểm M thỏa mãn →MA=→MB+→MC. Khẳng định nào sau đây đúng ?
A. Ba điểm C, M, B thẳng hàng.
B. AM là phân giác trong của góc ^BAC.
C. A, M và trọng tâm tam giác ABC thẳng hàng.
D. →AM+→BC=→0.
Đáp án đúng là: C
Gọi I, G lần lượt là trung điểm BC và trọng tâm tam giác ABC
Vì I là trung điểm BC nên →MB+→MC=2→MI.
Theo bài ra, ta có →MA=→MB+→MC suy ra thẳng hàng
Mặt khác G là trọng tâm của tam giác ABCA, M, G thẳng hàng.
Câu 15: Cho tam giác ABC có M là trung điểm của BC. Tính theo và
A.
B.
C.
D.
Đáp án đúng là: C
Ta có :