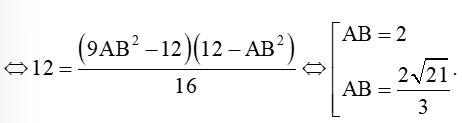50 câu Trắc nghiệm Giải tam giác (có đáp án 2024) – Toán 10 Cánh diều

Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 2: Giải tam giác đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 2.

1 80 lượt xem

Bài trước

Bài sau

Trắc nghiệm Toán 10 Bài 2: Giải tam giác

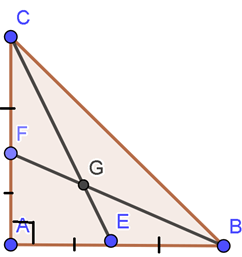
Câu 1. Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:

A. ${50 cm}^{2}$ ;

B. $50 \sqrt{2} {cm}^{2};$

C. ${75 cm}^{2}$ ;

D. $15 \sqrt{105} {cm}^{2}$ .

Hướng dẫn giải

Đáp án đúng là: C

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Vì F là trung điểm của AC $\Rightarrow$ $F C = \frac{1}{2} A C = 15 c m .$

Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.

Khi đó: $\frac{d (B; (A C))}{d (G; (A C))} = \frac{B F}{G F} = 3 \Rightarrow d (G; (A C)) = \frac{1}{3} d (B; (A C)) = \frac{A B}{3} = 10 c m .$

Vậy diện tích tam giác GFC là:

$S_{Δ G F C} = \frac{1}{2} . d (G; (A C)) . F C = \frac{1}{2} .10.15 = 75 c m^{2} .$

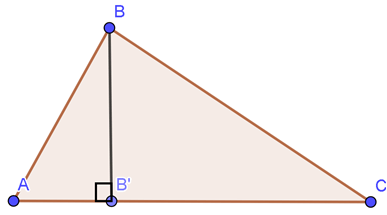
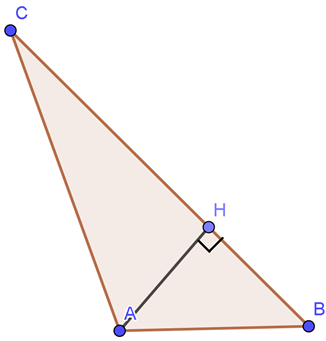
Câu 2. Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.

A. BB’ = 8;

B. $B B' = \frac{84}{5}$ ;

C. $B B' = \frac{168}{17}$ ;

D. $B B' = \frac{84}{17}$ .

Hướng dẫn giải

Đáp án đúng là: C

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Ta có:

Nửa chu vi là:

$p = \frac{21 + 17 + 10}{2} = 24$ (đơn vị độ dài).

Suy ra $S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$ (đơn vị diện tích).

Lại có $S = \frac{1}{2} b . B B' \Leftrightarrow 84 = \frac{1}{2} .17. B B' \Leftrightarrow B B' = \frac{168}{17}$ (đơn vị độ dài).

Câu 3. Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng 64 ${cm}^{2}$ . Giá trị sinAbằng:

A. $\sin A = \frac{\sqrt{3}}{2}$ ;

B. $\sin A = \frac{3}{8}$ ;

C. $\sin A = \frac{4}{5}$ ;

D. $\sin A = \frac{8}{9}$ .

Hướng dẫn giải

Đáp án đúng là: D

Ta có:

$S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{B A C} \Leftrightarrow 64 = \frac{1}{2} .8.18. \sin A \Leftrightarrow \sin A = \frac{8}{9} .$

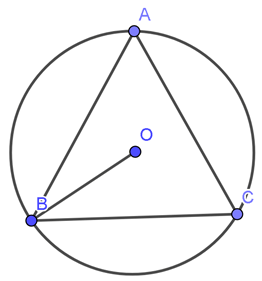
Câu 4. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:

A. $13 {cm}^{2}$ ;

B. $13 \sqrt{2} {cm}^{2}$ ;

C. $12 \sqrt{3} {cm}^{2};$

D. $15 {cm}^{2}$ .

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC đều, có độ dài cạnh bằng a.

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Theo định lí sin, ta có: $\frac{B C}{\sin \hat{B A C}} = 2 R \Leftrightarrow \frac{a}{\sin 60^{0}} = 2.4 \Leftrightarrow a = 8. \sin 60^{0} = 4 \sqrt{3}$ (đơn vị độ dài).

Vậy diện tích cần tính là:

$S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{B A C} = \frac{1}{2} . {(4 \sqrt{3})}^{2} . \sin 60^{0} = 12 \sqrt{3} c m^{2} .$

Câu 5. Tam giác ABC có $A C = 4, \hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 8$ ;

B. $S_{Δ A B C} = 4 \sqrt{3}$ ;

C. $S_{Δ A B C} = 4$ ;

D. $S_{Δ A B C} = 8 \sqrt{3}$ .

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $\hat{A B C} = 180^{0} - (\hat{B A C} + \hat{A C B}) = 75 ° = \hat{A C B}$ .

Suy ra tam giác ABC cân tại A nên AB = AC = 4.

Diện tích tam giác ABC là $S_{Δ A B C} = \frac{1}{2} A B . A C \sin \hat{B A C} = 4$ (đơn vị diện tích)

Câu 6. Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 9 \sqrt{3}$ ;

B. $S_{Δ A B C} = \frac{9 \sqrt{3}}{2}$ ;

C. $S_{Δ A B C} = 9$ ;

D. $S_{Δ A B C} = \frac{9}{2}$ .

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 60^{0} = \frac{9 \sqrt{3}}{2}$ (đơn vị diện tích)

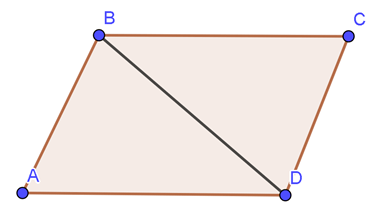
Câu 7. Hình bình hành ABCD có $A B = a, B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

A. $2 a^{2}$ ;

B. $a^{2} \sqrt{2}$ ;

C. $a^{2}$ ;

D. $a^{2} \sqrt{3}$ .

Hướng dẫn giải

Đáp án đúng là: C

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Diện tích tam giác ABD là: $S_{Δ A B D} = \frac{1}{2} . A B . A D . \sin \hat{B A D} = \frac{1}{2} . a . a \sqrt{2} . \sin 45^{0} = \frac{a^{2}}{2}$ (đơn vị diện tích).(BC = AD = a $\sqrt{2}$ )

Vậy diện tích hình bình hành ABCD là $S_{A B C D} = 2. S_{Δ A B D} = 2. \frac{a^{2}}{2} = a^{2}$ (đơn vị diện tích)

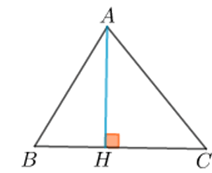
Câu 8. Tam giác ABC có $A C = 4, \hat{A C B} = 60 °$ . Tính độ dài đường cao hxuất phát từ đỉnh A của tam giác.

A. $h = 2 \sqrt{3}$ ;

B. $h = 4 \sqrt{3};$

C. $h = 2;$

D. $h = 4.$

Hướng dẫn giải

Đáp án đúng là: A

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Gọi H là chân đường cao xuất phát từ đỉnh A.

Xét tam giác vuông AHC:

$\sin \hat{A C H} = \frac{A H}{A C} \Rightarrow A H = A C . \sin \hat{A C H} = 4. \frac{\sqrt{3}}{2} = 2 \sqrt{3}$ (đơn vị độ dài)

Câu 9. Tam giác ABC có $B C = 2 \sqrt{3}, A C = 2 A B$ và độ dài đường cao AH = 2. Tính độ dài cạnh AB.

A. AB = 2;

B. $A B = \frac{2 \sqrt{3}}{3}$ ;

C. AB = 2 hoặc $A B = \frac{2 \sqrt{21}}{3}$ ;

D. AB = 2 hoặc $A B = \frac{2 \sqrt{3}}{3}$ .

Hướng dẫn giải

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Đáp án đúng là: C

Nửa chu vi là:

Ta có: $p = \frac{A B + B C + C A}{2} = \frac{2 \sqrt{3} + 3 A B}{2}$ .

Suy ra $S = \sqrt{(\frac{3 A B + 2 \sqrt{3}}{2}) (\frac{3 A B - 2 \sqrt{3}}{2}) (\frac{2 \sqrt{3} - A B}{2}) (\frac{2 \sqrt{3} + A B}{2})}$ .

Lại có $S = \frac{1}{2} B C . A H = 2 \sqrt{3}$ (đơn vị diện tích).

Từ đó ta có: $2 \sqrt{3} = (\frac{3 A B + 2 \sqrt{3}}{2}) (\frac{3 A B - 2 \sqrt{3}}{2}) (\frac{2 \sqrt{3} - A B}{2}) (\frac{2 \sqrt{3} + A B}{2})$

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Câu 10. Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 2S;

B. 3S;

C. 4S;

D. 6S.

Hướng dẫn giải

Đáp án đúng là: D

Diện tích tam giác ABC ban đầu là: $S = \frac{1}{2} . A C . B C . \sin \hat{A C B} = \frac{1}{2} . a b . \sin \hat{A C B} .$

Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là: $S_{Δ A B C} = \frac{1}{2} . (3 A C) . (2 B C) . \sin \hat{A C B} = 6. \frac{1}{2} . A C . B C . \sin \hat{A C B} = 6 S .$

Câu 11. Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

A. $60^{0}$ ;

B. $90^{0}$ ;

C. $150^{0}$ ;

D. $120^{0}$ .

Hướng dẫn giải

Đáp án đúng là: B

Diện tích tam giác ABC là: $S_{Δ A B C} = \frac{1}{2} . A C . B C . \sin \hat{A C B} = \frac{1}{2} . a b . \sin \hat{A C B} .$

Vì a, bdương và $\sin \hat{A C B} \leq 1$ nên suy ra $S_{Δ A B C} \leq \frac{a b}{2} .$

Dấu $" = "$ xảy ra khi và chỉ khi $\sin \hat{A C B} = 1 \Leftrightarrow \hat{A C B} = 90^{0} .$

Vậy giá trị lớn nhất của diện tích tam giác ABC là $S = \frac{a b}{2}$ (đơn vị diện tích).

Câu 12.Tam giác cân có cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là

A. $\frac{a^{2} \cos α}{2}$ ;

B. $\frac{a^{2} \sin α}{2}$ ;

C. $a^{2} \cos α$ ;

D. $a^{2} \sin α$ .

Hướng dẫn giải

Đáp án đúng là: B

Giả sử tam ABC cân taị C, ta có: AC = BC = a; $\hat{C}$ = $α$

Diện tích tam giác là: S = $\frac{1}{2}$ a.b.sinC = $\frac{1}{2}$ .a.a.sin $α$ = $\frac{1}{2}$ $a^{2}$ sin $α$ .

Câu 13. Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 30 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 9 \sqrt{3}$ ;

B. $S_{Δ A B C} = \frac{9 \sqrt{3}}{2}$ ;

C. $S_{Δ A B C} = 4, 5$ ;

D. $S_{Δ A B C} = \frac{9}{2}$ .

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 30^{0} = \frac{9.1}{2}$ = 4,5 (đơn vị diện tích).

Câu 14. Tam giác ABC có a = 21, b = 17, c = 10 .Diện tích của tam giác ABC bằng:

A. $S_{Δ A B C} = 16$ ;

B. $S_{Δ A B C} = 48$ ;

C. $S_{Δ A B C} = 24$ ;

D. $S_{Δ A B C} = 84$ .

Hướng dẫn giải

Đáp án đúng là: D

Ta có:

Nửa chu vi của tam giác ABC là:

$p = \frac{21 + 17 + 10}{2} = 24$ (đơn vị độ dài).

Do đó

Diện tích tam giác ABC là:

$S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$ (đơn vị diện tích).

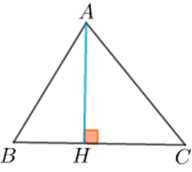
Câu 15. Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính độ dài đường cao hkẻ từ đỉnh A xuống cạnh BC của tam giác.

A. $h = 3 \sqrt{3}$ ;

B. $h = \sqrt{3}$ ;

C. $h = 3$ ;

D. $h = \frac{3}{2}$ ;

Hướng dẫn giải

Đáp án đúng là: C

15 Bài tập Giải tam giác. Tính diện tích tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Áp dụng định lý hàm số cosin, ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C \cos A = 27 \Rightarrow B C = 3 \sqrt{3}$ (đơn vị độ dài).

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 60^{0} = \frac{9 \sqrt{3}}{2}$ (đơn vị diện tích).

Lại có $S_{Δ A B C} = \frac{1}{2} . B C . h_{a} \Rightarrow h_{a} = \frac{2 S}{B C} = 3$ (đơn vị độ dài).

1 80 lượt xem

Bài trước

Bài sau

50 câu Trắc nghiệm Giải tam giác (có đáp án 2024) – Toán 10 Cánh diều

Giới thiệu

Liên kết

Chính sách

Kết nối

50 câu Trắc nghiệm Giải tam giác (có đáp án 2024) – Toán 10 Cánh diều

CHỌN BỘ SÁCH BẠN MUỐN XEM