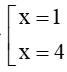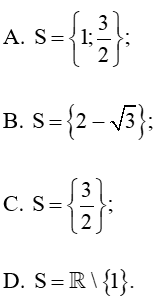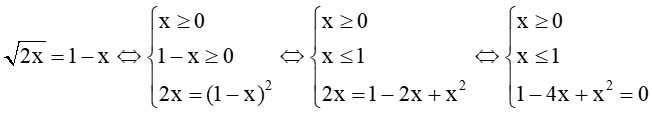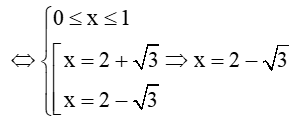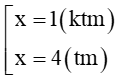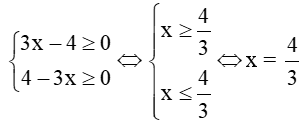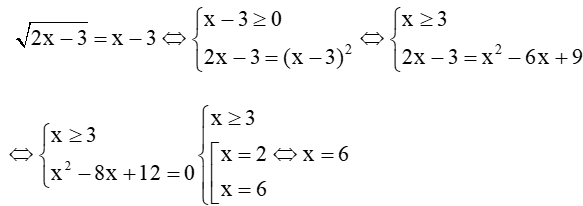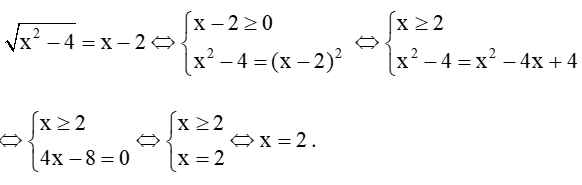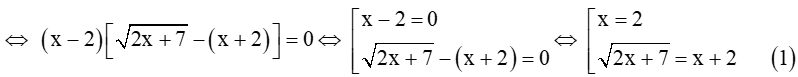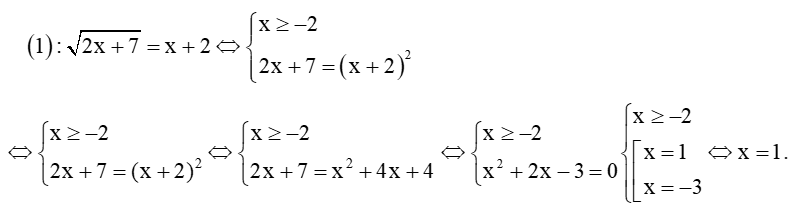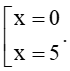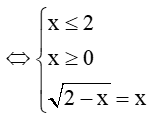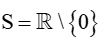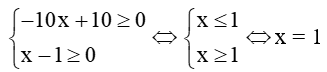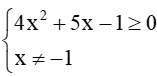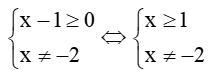50 câu Trắc nghiệm Hai dạng phương trình quy về phương trình bậc hai (có đáp án 2024) – Toán 10 Cánh diều
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 5: Hai dạng phương trình quy về phương trình bậc hai đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 5.
Trắc nghiệm Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Câu 1. Tập nghiệm S của phương trình √2x+x−1=0 là:
Đáp án đúng là: B
Điều kiện:x≥0
Khi đó phương trình có thể viết lại như sau:
Câu 2. Tập nghiệm S của phương trình 2x2+5x−1√x−1=x+5√x−1 là:
A. S = {1};
B. S=∅;
C. S=ℝ;
D. S = {-3}
Đáp án đúng là: B
Điều kiện: x - 1 > 0⇔x > 1
Phương trình có thể viết lại như sau: 2x2+5x−1=x+5⇔2x2+4x−6 = 0
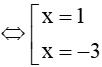
Câu 3. Tập nghiệm của phương trình x2−5x√x−2=−4√x−2 là:
A. S=(1;4);
B. S=(1);
C. S=∅;
D. S=(4).
Đáp án đúng là: D
Điều kiện x>2.
Khi đó phương trình ⇔x2−5x√x−2=−4√x−2⇔x2−5x+4=0⇔
Do đó, S = {4}.
Câu 4.Nghiệm của phương trình √3x−4=√4−3x là đáp án nào trong số các đáp án sau đây?
A. x = 1
B. x = 2
C. x = 3
D. x = 43
Đáp án đúng là: D
Điều kiện:
Bình phương hai vế của phương trình ta có: 3x - 4 = 4 - 3x⇔6x = 8 ⇔x = 43.
Đối chiếu với điều kiện bài toán và thử lại kết quả suy ra phương trình có nghiệm
x = 43.
Câu 5. Tập nghiệm của phương trình x+1√x+1=√x+1là?
A. S = (-1; 1)
B. S = (1; +∞)
C. S = {-1}
D. S = (-1; 0)
Đáp án đúng là: B
Điều kiện: x + 1 > 0⇔x > -1
Khi đó phương trình có thể viết lại như sau: x + 1 = x + 1 (luôn đúng)
Như vậy tập nghiệm của phương trình là khoảng (-1; +∞).
Câu 6. Tập nghiệm S của phương trình √2x−3=x−3 là:
A. S=(6;2);
B. S=(2);
C. S=(6);
D. S=∅.
Đáp án đúng là: C
Ta có :
Câu 7. Tập nghiệm S của phương trình √x2−4=x−2là:
A. S=(0;2);
B. S=(2);
C. S=(0);
D. S=∅.
Đáp án đúng là: B
Ta có:
Câu 8. Tổng các nghiệm của phương trình (x−2)√2x+7=x2−4 bằng:
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án đúng là: D
Điều kiện xác định của phương trình 2x+7≥0⇔x≥−72.
Ta có : (x−2)√2x+7=x2−4⇔(x−2)√2x+7=(x−2)(x+2)
Giải phương trình
Vậy phương trình đã cho có hai nghiệm x=1,x=2 nên tổng hai nghiệm của phương trình là
Câu 9. Phương trình x2−4x−2√x−2=√x−2 có tất cả bao nhiêu nghiệm?
A. 1;
B. 2;
C. 3;
D. 5.
Đáp án đúng là: A
Điều kiện xác định của phương trình x−2>0⇔x>2.
Từ phương trình đã cho ta được: x2−4x−2=x−2⇔x2−5x=0⇔
So với điều kiện x > 2 thì x = 5 là nghiệm duy nhất của phương trình.
Câu 10. Phương trình √2−x+4√2−x+3=2 có tất cả bao nhiêu nghiệm?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án đúng là: B
Điều kiện xác định của phương trình 2−x≥0⇔x≤2.
Từ phương trình đã cho ta được :
√2−x(√2−x+3)+4=2(√2−x+3)
⇔2−x+3√2−x+4=2√2−x+6
⇔3√2−x−2√2−x=−2+x−4+6
⇔√2−x=x
⇔2−x=x2⇔x2+x−2=0
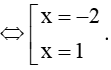
Câu 11. Tập nghiệm S của phương trình 3x2−7x+2√3x−1=√3x−1 là:
A. S=∅;
B. S = {1};
C. S = {3};
D.
Đáp án đúng là: C
Điều kiện: 3x - 1 > 0⇔x > 13
Khi đó phương trình được viết lại như sau: 3x2−7x+2=(√3x−1)2⇔3x2−7x+2=3x−1⇔3x2−10x+3=0
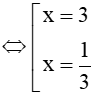
Câu 12.Nghiệm của phương trình √−10x+10=x−1là:
A. x = -12;
B. x = -6;
C. x = 1;
D. x = 2
Đáp án đúng là: C
Điều kiện:
Khi đó phương trình có thể viết lại như sau: −10x+10=(x−1)2⇔−10x+10=x2−2x+1⇔x2+8x−9 = 0
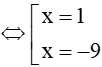
Câu 13. Phương trình √4x2+5x−1x+1=√2 có nghiệm là?
A. x = 0;
B. x = 1;
C. x = 2;
D. x = 4.
Đáp án đúng là: B
Điều kiện:
Khi đó phương trình được viết thành: √4x2+5x−1=√2.(x+1)
⇔4x2+5x−1=2.(x+1)2⇔2x2+x−3 = 0 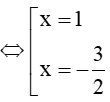
Câu 14. Tập nghiệm S của phương trình √x−1x+2=−x−11x+2+2 là:
A. S=(−1;1);
B. S=(−1);
C. S=(1);
D. S = {10}.
Đáp án đúng là: D
Điều kiện:
Khi đó phương được viết thành:√x−1x+2=x−7x+2⇒√x−1=x−7
⇔x−1=(x−7)2⇔x2−15x+50 = 0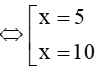
Câu 15.Nghiệm của phương trình x2−4x+3√x−1=√x−1 là:
A. 0;
B. 1;
C. 2;
D. 4;
Đáp án đúng là: D
Điều kiện: x - 1 > 0⇔x > 1.
Phương trình có thể viết lại như sau: x2−4x+3=x−1⇔x2−5x+4 = 0
⇔