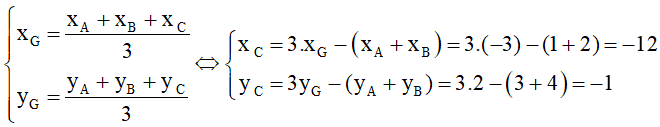50 câu Trắc nghiệm Vectơ trong mặt phẳng tọa độ (có đáp án 2024) – Toán 10 Kết nối tri thức
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 10: Vectơ trong mặt phẳng tọa độ đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 10.
Trắc nghiệm Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ
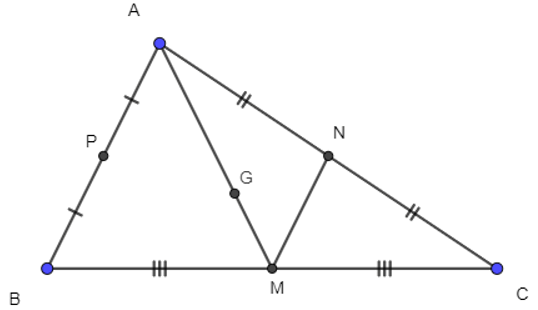
Câu 1. Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
A. G(13;1);
B. G(1; 3);
C. G(2; -3);
D. G(1; 1).
Đáp án đúng là A
Ta có →MN=→PA = (-1; 4)
Gọi tọa độ của điểm A là A(xA; yA). Khi đó →PA(xA−2;yA+3).
Ta có →MN=→PA (tính chất đường trung bình)
Suy ra {xA−2=−1yA+3=4⇔{xA=1yA=1
⇒ A(1; 1).
Gọi tọa độ điểm B, C lần lượt là B(xB; yB) và C(xC; yC).
Vì P là trung điểm của AB nên ta có: {xB=2.2−1yB=2.(−3)−1⇔{xB=3yB=−7
⇒ B(3; -7).
Vì N là trung điểm của AC nên ta có: {xC=2.(−1)−1yC=2.5−1⇔{xC=−3yC=9
⇒ C(-3; 9).
Khi đó tọa độ trọng tâm G là {xG=1+3+(−3)3yG=1+(−7)+93⇔{xG=13yG=1
⇒G(13;1).
Câu 2. Trong mặt phẳng tọa độ Oxy, cho các vecto →b(4;−1) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để →MN=→b.
A. x = 0, y = 0;
B. x = 13, y = 43;
C. x = 0, y = 43;
D. x = 43, y = 0.
Đáp án đúng là D
Ta có: →MN=(0−(−3x);−2+y−(−1))=(3x;−1+y)
Để →MN=→b⇔{3x=4−1+y=−1⇔{x=43y=0.
Vậy x = 43, y = 0.
Câu 3. Trong mặt phẳng tọa độ Oxy, cho các điểm A(k−13;5), B(-2; 12) và
C(23;k−2). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
A. (10; 12);
B. (-2; 0);
C. (14; 15);
D. (12; 14).
Đáp án đúng là
Ta có: →AC=(23−(k−13);k−2−5)=(1−k;k−7),
→BC=(23−(−2);k−2−12)=(83;k−14)
Để ba điểm A, B, C thẳng hàng khi →AC và →BC cùng phương
⇔1−k83=k−7k−14
⇔ (1 – k)(k – 14) = 83(k – 7)
⇔ - k2 + 15k – 14 = 83k – 563
⇔ - 3k2 + 45k – 42 = 8k – 56
⇔ 3k2 – 37k – 14 = 0
⇔ k1 ≈ 12,7 hoặc k2 ≈ -0,37.
Ta thấy k1 là giá trị dương nằm trong khoảng (12; 14).
Câu 4. Trong mặt phẳng tọa độ Oxy, cho →u=−5→i+6→j. Khi đó tọa độ của vectơ →u là:
A. →u(5; 6);
B. →u(-5; -6);
C. →u(6; -5);
D. →u(-5; 6).
Đáp án đúng là D
Ta có →u=−5→i+6→j. Khi đó toạ độ của →u là →u(-5; 6).
Câu 5. Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài →BC là:
A. 5;
B. 3;
C. √13;
D. √15.
Đáp án đúng là C
Ta có →BC = (3 – 1; -1 – 2) = (2; -3).
⇒|→BC|=√22+(−3)2=√13.
Câu 6. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
A. M(1; 2);
B. M(-1; 2);
C.M(1; -2);
D. M(-1; -2)
Đáp án đúng là A
Ta có hai vecto →OA(2;1),→OB(3;3) không cùng phương (vì 23≠13). Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Suy ra các điểm O, A, B không thẳng hàng
Để OABM là hình bình hành khi và chỉ khi →OA=→MB
Ta có: →OA(2;1),→MB(3−x;3−y) nên
{2=3−x1=3−y⇔{x=1y=2⇒M(1;2).
Vậy điểm cần tìm là M(1;2).
Câu 7. Trong mặt phẳng tọa độ Oxy, cho các vecto →u(2;3x−3) và →v(−1;−2). Có bao nhiêu giá trị nguyên của x thỏa mãn |→u|=|2→v|.
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án đúng là A
Độ dài của vectơ |→u|=√22+(3x−3)2=√4+(3x−3)2.
Độ dài của vectơ |→v|=√(−1)2+(−2)2=√5.
Suy ra độ dài của vectơ 2|→v|=2.√(−1)2+(−2)2=2√5.
Để |→u| = 2|→v| thì √4+(3x−3)2=2√5
⇔ 4 + (3x – 3)2 = 20
⇔ (3x – 3)2 = 16
⇔ [3x+3=43x+3=−4
⇔ [3x=13x=−7
⇔ [x=13x=−73
Ta thấy các giá trị 13 hay −73 đều không là các giá trị nguyên. Do đó không tồn tại giá trị nguyên nào của x thỏa mãn điều kiện đầu bài.
Câu 8. Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
→x(-1; 3); →y(2;−13); →z(−25;15); →w(4; -2).
A. Có 1 cặp;
B. Có 3 cặp;
C. Có 4 cặp;
D. Có 0 cặp.
Đáp án đúng là A
+) Xét cặp vectơ →z và →w ta có: −254=15−2. Do đó cặp vectơ →z và →w cùng phương.
Các cặp vectơ còn lại không cùng phương, thật vậy
+) Xét cặp vectơ →y và →z ta có: 2−25≠−1315. Do đó cặp vectơ →y và →z không cùng phương.
Vì cặp vectơ →z và →w cùng phương nên cặp vectơ →y và →w không cùng phương.
+) Xét cặp vectơ →y và →x ta có: 2−1≠−133. Do đó cặp vectơ →y và →x không cùng phương.
+) Xét cặp vectơ →x và →z ta có: −1−25≠315. Do đó cặp vectơ →x và →z không cùng phương.
Vì cặp vectơ →z và →w cùng phương nên cặp vectơ →x và →w không cùng phương.
Vậy chỉ có duy nhất một cặp vectơ cùng phương
Câu 9. Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
A. Tam giác OMN là tam giác đều;
B. Tam giác OMN vuông cân tại M;
C. Tam giác OMN vuông cân tại N;
D. Tam giác OMN vuông cân tại O.
Đáp án đúng là B
Ta có M(1;3) ⇒→OM(1;3)⇒OM=√12+32=√10.
Ta lại có N(4;2) ⇒→ON(4;2)⇒ON=√42+22=√20=2√5.
⇒→MN=→ON−→OM=(−3;1)⇒MN=√(−3)2+12=√10
Xét tam giác OMN, có: OM=MN=√10 nên tam giác OMN cân tại M.
Ta có: ON2=(2√5)2=20,OM2+MN2=(√10)2+(√10)2=20
⇒ON2=OM2+MN2
Theo định lí Py – ta – go đảo suy ra tam giác OMN vuông tại O.
Do đó tam giác OMN vuông cân tại M.
Câu 10. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
A. C(0; 3);
B. C(-6; -5);
C. C(-12; -1);
D. C(0; 9).
Đáp án đúng là C
Vì G là trọng tâm tam giác ABC nên ta có:
⇒ G(-12; -1).
Câu 11. Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto →v=(2;5). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
A. (-1; 7);
B. (4; 10);
C. (1; 12);
D. Không xác định được vị trí của tàu.
Đáp án đúng là C
Gọi A’(x’; y’) là vị trí tàu thủy đến sau khi khởi hành 2 giờ.
Khi đó, ta có:
{x'
Vậy sau khi khởi hành 2 giờ thì tàu thủy đến được vị trí A’(1; 12).
Câu 12. Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
A. P(0; 13);
B. Q(1; -8);
C. H(2; 1);
D. K(3; 1).
Đáp án đúng là B
Ta có . Gọi tọa độ điểm cần tìm là F(x; y).
Khi đó
Để M, N, F thẳng hàng khi cùng phương với hay
⇔ y + 1 = 4(x – 3)
⇔ y= 4x – 12 (1)
+) Xét tọa độ P có x = 0 và y = 13 thay vào (1) ta được 13 = 4.0 – 12 là mệnh đề sai. Do đó loại P.
+) Xét tọa độ Q có x = 1 và y = -9 thay vào (1) ta được -8 = 4.1 – 12 là mệnh đề đúng. Do đó Q thỏa mãn.
+) Xét tọa độ H có x = 2 và y = 1 thay vào (1) ta được 1 = 4.2 – 12 là mệnh đề sai. Do đó loại H.
+) Xét tọa độ K có x = 3 và y = 1 thay vào (1) ta được 1 = 4.3 – 12 là mệnh đề sai. Do đó loại H.
Vậy M, N, Q thẳng hàng.
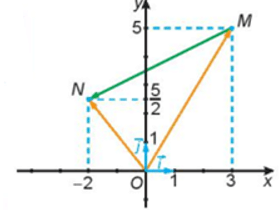
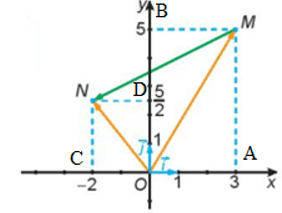
Câu 13. Cho hình vẽ sau:
Hãy biểu thị mỗi vecto theo các vecto .
A. và ;
B. và ;
C. và ;
D. và .
Đáp án đúng là A
Xét hình bình hành OAMB, có:
(quy tắc hình bình hành)
Xét hình bình hành OCND, có:
(quy tắc hình bình hành) .
Câu 14. Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
A. Tam giác ABD
B. Tam giác ABC
C. Tam giác ACD
D. Tam giác BCD
Đáp án đúng là D
+) Trọng tâm tam giác ABD là: ;
+) Trọng tâm tam giác ABC là: ;
+) Trọng tâm tam giác ACD là: ;
+) Trọng tâm tam giác BCD là: = (3; 6).
Vậy G là trọng tâm tam giác BCD.
Câu 15. Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2). Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD. Tổng x + y bằng
A. 10;
B. -10;
C. 3;
D. -3.
Đáp án đúng là B
Để O(0;0) là tọa độ trọng tâm tam giác ABD thì:
Suy ra D(-3;-7) thì O(0;0) là trọng tâm tam giác ABD.
Vậy tổng x + y = -3 + (-7) = -10.