50 câu Trắc nghiệm Giá trị lượng giác của 1 góc từ 0° đến 180° (có đáp án 2024) – Toán 10 Kết nối tri thức
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 5: Giá trị lượng giác của 1 góc từ 0° đến 180° đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 5.
Trắc nghiệm Toán 10 Bài 5: Giá trị lượng giác của 1 góc từ 0° đến 180°
I. Nhận biết
Câu 1. Giá trị cos90° + sin90° bằng bao nhiêu ?
A. 0;
B. 1;
C. – 1;
D. 2.
Đáp án: B
Giải thích:
Sử dụng máy tính cầm tay ta tính được: cos90° + sin90° = 1
Câu 2. Cho α và β là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sinβ = – sinα;
B. cosβ = cosα;
C. tanβ = tanα;
D. cotβ = – cotα.
Đáp án: D
Giải thích:
Hai góc bù nhau có sin bằng nhau, côsin, tang, côtang đối nhau.
Câu 3. M là điểm trên nửa đường tròn lượng giác sao cho ^xOM= 90°. Tọa độ điểm M là
A. (1;0);
B. (0;1);
C. (1;1);
D. ( –1;0).
Đáp án: B
Giải thích:
Định nghĩa tỉ số lượng giác của 1 góc bất kì từ 0° đến 180°: Với góc α cho trước,
0° ≤ α ≤ 180°. Gọi M(x0;y0) là điểm trên nửa đường tròn đơn vị nói trên sao cho ^xOM = α. Ta có:
+ Sin của góc α là tung độ y0 của điểm M kí hiệu là sinα.
+ Côsin của góc α là hoành độ x0 của điểm M kí hiệu là cosα
Vậy tọa độ M là (cos90°; sin90°) = (0 ; 1).
Câu 4. Khẳng định nào sau đây đúng ?
A. sin( 180° – α ) = – sinα;
B. cos( 180° – α ) = cosα;
C. sin( 90° – α ) = – cosα;
D. cos( 90° – α ) = sinα.
Đáp án: D
Giải thích:
Hai góc bù nhau có sin bằng nhau, côsin, tang, côtang đối nhau.
Khi đó ta có:
sin( 180° – α ) = sinα;
cos( 180° – α ) = – cosα.
Do đó A và B sai.
Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Khi đó ta có:
sin( 90° – α ) = cosα;
cos( 90° – α ) = sinα.
Do đó C sai và D đúng.
Câu 5. Khẳng định nào sau đây đúng ?
A. cos2x+sin2x=1;
B. cos2x+sin2x=0;
C. cos2x+sin2x=2;
D. cos2x+sin2x=14.
Đáp án: A
Giải thích:
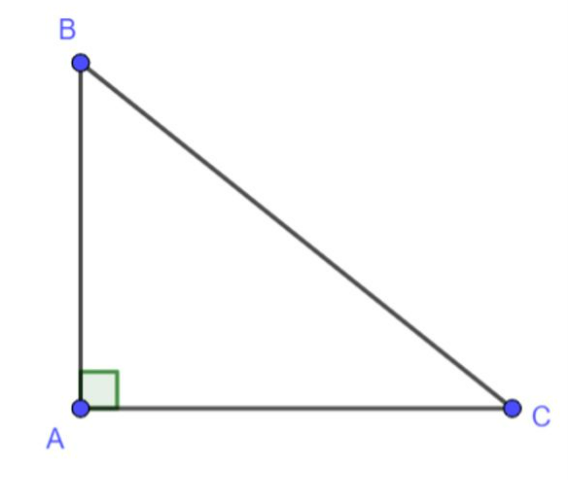
Giả sử = x.
Ta có cosx = ABBC; sinx = ACBC.
cos2x + sin2x= AB2BC2+AC2BC2=BC2BC2=1.
Câu 6. Khẳng định nào sau đây đúng ?
A. sin45° = –√22;
B. cos45° = 1;
C. tan45° = 1;
D. cot45° = √22.
Đáp án: C
Giải thích:
Sử dụng máy tính cầm tay ta tính được:
sin45° = √22; cos45° = √22; tan45° = 1; cot45° = 1.
Do đó A, B, D sai và C đúng.
Câu 7. M là điểm trên nửa đường trong lượng giác sao cho ^xOM= α. Tọa độ của điểm M là:
A. (sin α; cos α);
B. (cos α; sin α);
C. (– sin α; cos α);
D. ( – cos α; – sin α).
Đáp án: B
Giải thích:
Định nghĩa tỉ số lượng giác của 1 góc bất kì từ 0° đến 180°:
Với góc α cho trước, 0° ≤ α ≤ 180°.
Gọi M(x0;y0) là điểm trên nửa đường tròn đơn vị nói trên sao cho ^xOM = α. Ta có:
+ Sin của góc α là tung độ y0 của điểm M kí hiệu là sinα.
+ Côsin của góc α là hoành độ x0 của điểm M kí hiệu là cosα.
II. Thông hiểu
Câu 1. Cho P = (sinα + cosβ)(sinα − cosβ) + (cosα + sinβ)(cosα − sinβ)
Giá trị của biểu thức P là?
A. 1;
B. 0;
C. 2;
D. 3.
Đáp án: B
Giải thích:
P = ( sinα + cosβ)(sinα − cosβ) + (cosα + sinβ)(cosα − sinβ)
⇔ P =sin2α–cos2β+cos2α–sin2β
⇔ P = 0
Câu 2. Tính giá trị biểu thức S = sin235° + cos225° + sin255° + cos265°.
A. 3;
B. 2;
C. 1;
D. 0.
Đáp án: B
Giải thích:
Sử dụng: sin( 90° – α ) = cosα và cos( 90° – α ) = sinα
S = sin235° + cos225° + sin255° + cos265°
⇔ S = sin235° + cos225° + [ sin(90° – 35°)]2 + [ cos(90° – 25°)]2
⇔ S = sin235° + cos225° + cos235° + sin225°
⇔ S = ( sin235° + cos235° ) + ( cos225° + sin225° )
⇔ S = 2.
Câu 3. Biểu thức P = tan15°.tan25°.tan35°.tan55°.tan65°.tan75° có giá trị bằng?
A. 2;
B. –1;
C. 1;
D. 0.
Đáp án: C
Giải thích:
Sử dụng công thức: tan( 90° – α ) = cotα và tanα =1cotα hay tanα.cotα = 1
P = tan15°.tan25°.tan35°.tan55°.tan65°.tan75°
⇔ P = tan15°.tan25°.tan35°.cot35°.cot25°.cot15°
⇔ P = (tan15°.cot15°)(tan25°.cot25°).(tan35°.cot35°)
⇔ P = 1.1.1
⇔ P = 1.
Câu 4. Cho góc α thỏa mãn cos2α=16. Khẳng định nào sau đây là đúng?
A. 1 + cot2α = 6;
B. 1 + cot2α = 5;
C. 1 + tan2α = 5;
D. 1 + tan2α = 6.
Đáp án: D
Giải thích:
Sử dụng cos2α + sin2α = 1 ⇒sin2α=56⇒ tan2α = 5 và cot2α = 1
⇒ 1 + tan2α = 6 và 1 + cot2α = 2.
Vậy đáp án D đúng.
Câu 4. Tính giá trị biểu thức A = cot20° + cot40° + cot60° + .... + cot160°
A. 1;
B. 2;
C. 0;
D. 4.
Đáp án: C
Giải thích:
Sử dụng cot( 180° – α ) = – cotα với 0° < α < 180°
Hay cot( 180° – α ) + cotα = 0
A = ( cot20° + cot160°) + ( cot40° + cot140°) + ( cot60° + cot120°) + ( cot80° + cot100°)
⇔ A = 0
Câu 5. Tính giá trị biểu thức P = sin30°.cos15° + sin150°.cos165°
A. 0;
B. 1;
C. – 1;
D. 0,5.
Đáp án: A
Giải thích:
Sử dụng công thức: sin( 180° – α ) = sinα và cos( 180° – α ) = – cosα.
Có sin30° = sin150°; cos15° = – cos165°
P = sin30°.cos15° – sin30°.cos15°= 0
Câu 6. Cho tam giác ABC. Tính P = sinA.cos(B + C) + sin(B + C).cosA
A. 0;
B. 1;
C. -1;
D. 0,5.
Đáp án: A
Giải thích:
Giả sử: ⏜A= α; ˆB+ˆC=β. Do ⏜A,ˆB,ˆC là 3 góc trong tam giác nên α + β = 180°
⇒ β = 180° – α
⇒ sinβ = sin(180° – α) = sinα và cosβ = cos( 180° – α ) = – cosα
P = sinA.cos(B + C) + sin(B + C).cosA = sinα.cosβ + sinβ.cos α = sinα.(–cosα) + sinα.cos α = 0.
Câu 8. Cho góc α biết sinα + cosα = 54. Tính A = sinα.cosα
A. 932;
B. 732;
C. 239;
D. 937.
Đáp án: A
Giải thích:
(sinα+cosα)2=sin2α+cos2α+2sinα.cosα=1+2sinαcosα=2516
⇔ sinα.cosα=2516−12=932.
III. Vận dụng
Câu 1. Tính giá trị biểu thức A = cotα – 2tanαtanα + 3cotα với sinα = 35.
A. −257;
B. 257;
C. 557;
D. −557.
Đáp án: A
Giải thích:
Ta có: cosαsinα–2sinαcosαsinαcosα+3cosαsinα=cos2α–2sin2αsin2α+3cos2α=1–3sin2α3–2sin2α=1−3.(35)23−2.(35)2=−257.
Câu 2. Cho 3cosα – sinα = 1; 0° < α < 90°. Tính tanα.
A. 43;
B. 34;
C. 45;
D. 54.
Đáp án: A
Giải thích:
3cosα – sinα = 1
⇔ 3cosα = 1 + sinα
⇒ 9cos2α = (sinα + 1)2 = sin2α + 2.sin α +1
⇒ 9 – 9sin2 α = sin2α + 2.sin α +1
⇒ 10 sin2α + 2.sinα – 8 = 0
⇒ sinα = – 1 hoặc sinα = 45
Với sinα = – 1 không thỏa mãn 0<α<90°
Với sinα = 45⇒ cosα = 35.
Vậy tanα =43
Câu 3. Cho biết tanα = – 3. Tính giá trị P = 6sinα–7cosα6cosα+7sinα
A. 53;
B. 13;
C. 43;
D. 23.
Đáp án: A
Giải thích:
Có: tanα=sinαcosα=–3 ⇒ sinα = – 3cosα
P = 6sinα–7cosα6cosα+7sinα = 6.(–3)cosα–7cosα6cosα+7.(–3)cosα=–25–15=53
Câu 4. Cho biết sinα = 35. Tính giá trị của P = 3sin2α + 5cos2α
A. 10325;
B. 10725;
C. 10925;
D. 11125.
Đáp án: B
Giải thích:
Sử dụng công thức: cos2α + sin2α = 1
P = 3sin2α+5cos2α = 5sin2α+5cos2α–2sin2α=5–2.3252=10725
Câu 5. Cho biết 2cosα+√2sinα=2. Tính cotα biết 0° < α < 90°.
A. √54;
B. √34;
C. √24;
D. √22.
Đáp án: C
Giải thích:
2cosα + √2sinα = 2 ⟺ √2sinα = 2 – 2cosα ⇒ 2sin2α = 4 – 8cos + 4 cos2α
⟹ 2 – 2cos2α = 4 – 8cosα + 4cos2α
⟹ 6cos2 α – 8cosα + 2 = 0
cosα = 1 không thỏa mãn 0° < α < 90°.
cosα = 13⇒ cotα= √24.