50 câu Trắc nghiệm Đường tròn mặt phẳng toạ độ (có đáp án 2024) – Toán 10 Kết nối tri thức
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 21: Đường tròn mặt phẳng toạ độ đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 21.
Trắc nghiệm Toán 10 Bài 21: Đường tròn mặt phẳng toạ độ
I. Nhận biết
Câu 1. Cho đường tròn (C) : (x + 1)2 + (y − √2)2 = 8. Tâm I của đường tròn là:
A. I(−1; √2);
B. I(1; − √2);
C. I(1; √2);
D. . I(−1; − √2);.
Đáp án: A
Giải thích:
Lí thuyết: Phương trình đường tròn tâm I(a; b) và bán kính R là:
(x − a)2 + (y − b)2 = R2
Vậy với phương trình (x + 1)2 +(y − √2)2 = 8 có a = −1;b = √2 nên I(−1; √2)
Câu 2. Cho đường tròn (C): x2 + y2 = 9. Bán kính R của đường tròn là:
A. R = 9;
B. R = 81;
C. R = 6 ;
D. R = 3.
Đáp án: D
Giải thích:
Đường tròn: x2 + y2 = 9 có bán kính R = √9 = 3.
Câu 3. Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi
A. a2 + b2 > 0;
B. a2 + b2 − c = 0;
C. a2 + b2 − c < 0;
D. a2 + b2 − c > 0.
Đáp án: D
Giải thích:
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi a2 + b2 − c > 0
Câu 4. Phương trình đường tròn tâm I(3; −5) , bán kính R = 2 là:
A. x2 + y2 + 3x – 5y + 2 = 0;
B. x2 + y2 + 6x – 10y + 30 = 0;
C. x2 + y2 – 6x + 10y – 4 = 0;
D. x2 + y2 – 6x + 10y + 30 = 0.
Đáp án: D
Giải thích:
Phương trình đường tròn tâm I(3; −5) , bán kính R = 2 là:
(x – 3)2 + (y + 5)2 = 22
⇔ x2 – 6x + 9 + y2 + 10y + 25 = 4
⇔ x2 + y2 – 6x + 10y + 30 = 4.
Câu 5. Đường tròn (C): x2 + y2 – 6x + 2y + 6 = 0 có tâm I và bán kính R lần lượt là:
A. I(3; −1) và R = 4;
B. I(3; 1) và R = 4;
C. I(3; −1) và R = 2;
D. I(-6; 2) và R = 2.
Đáp án: C
Giải thích:
Ta có: x2 + y2 – 6x + 2y + 6 = 0 ⇔ x2 + y2 – 2.3x – 2.(−1).y + 6 = 0
⇒ a = 3 ; b = −1 ; c = 6
Vậy đường tròn (C) có tâm I(3; −1) và R = √a2+b2−c = √32+(−1)2−6 = 2.
II. Thông hiểu
Câu 1. Phương trình đường tròn tâm I(1; −5) và đi qua điểm M(4; -1) là:
A. (x – 1)2 + (y + 5)2 = 25;
B. (x – 4)2 + (y + 1)2 = 25;
C. (x + 1)2 + (y – 5)2 = 25;
D. (x + 4)2 + (y – 1)2 = 25.
Đáp án: A
Giải thích:
Phương trình đường tròn tâm I(1; −5) có dạng: (x – 1)2 + (y + 5)2 = R2
Vì đường tròn (C) đi qua điểm M(4; -1) nên: (4 – 1)2 + (–1+ 5)2 = R2
⇔ R2 = 25
Vậy phương trình đường tròn (C) là: (x – 1)2 + (y + 5)2 = 25.
Câu 2. Cho hai điểm A(8; 0) và B(0; 6). Phương trình đường tròn ngoại tiếp tam giác OAB là:
A. x2 + (y – 6)2 = 25 ;
B. (x – 8)2 + y2 = 25;
C. (x – 4)2 + (y – 3)2 = 25;
D. (x + 4)2 + (y + 3)2 = 25.
Đáp án: C
Giải thích:
Ta có: A ∈ Ox và B ∈ Oy nên tam giác OAB vuông tại O
Do đó tâm I của đường tròn ngoại tiếp tam giác OAB là trung điểm của AB nên I (4; 3)
Mặt khác ta có: R = IA = √(8−4)2+(0−3)2=5
Vậy phương trình đường tròn ngoại tiếp tam giác OAB là: (x – 4)2 + (y – 3)2 = 25.
Câu 3. Phương trình đường tròn tâm I(– 2; 1) và tiếp xúc đường thẳng ∆: x – 2y + 7 = 0 là:
A. (x + 1)2 + (y – 2)2 = 2√5;
B. (x – 1)2 + (y + 2)2 = 2√5;
C. (x – 1)2 + (y + 2)2 = 45;
D. (x + 1)2 + (y – 2)2 = 45.
Đáp án: D
Giải thích:
Bán kính đường tròn (C) là khoảng cách từ I đến đường thẳng ∆ nên
R = d(I; ∆) = |−1−4−7|√1+4=2√5
Vậy phương trình đường tròn (C) là: (x + 1)2 + (y – 2)2 = 45.
Câu 4. Phương trình nào sau đây không là phương trình đường tròn?
A. x2 + y2 – x + y + 4 = 0;
B. x2 + y2 – y = 0 ;
C. x2 + y2 – 2 = 0;
D. x2 + y2 – 100y + 1 = 0.
Đáp án: A
Giải thích:
+ Xét phương trình x2 + y2 – x + y + 4 = 0 có a = 12 ; b = −12 ; c = 4
Ta có: a2 + b2 – c = (12)2+(−12)2−4=−72<0
nên phương trình x2 + y2 – x + y + 4 = 0 không là phương trình đường tròn.
+ Xét phương trình x2 + y2 – y = 0 có a = 0; b = 12 ; c = 0
Ta có: a2 + b2 – c = (12)2>0 nên phương trình x2 + y2 – y = 0 là phương trình đường tròn.
+ Xét phương trình x2 + y2 – 2 = 0 có a = 0; b = 0; c = -2
Ta có: a2 + b2 – c = nên phương trình x2 + y2 – 2 = 0 là phương trình đường tròn.
+ Xét phương trình x2 + y2 – 100y + 1 = 0 có a = 0; b = 50; c = 1.
Ta có: a2 + b2 – c = nên phương trình x2 + y2 – 100y + 1 = 0 là phương trình đường tròn.
Câu 5. Đường tròn x2 + y2 – 2x + 10y + 1 = 0 đi qua điểm nào trong các điểm sau đây?
A. A(2; 1);
B. B(3; −2)
C. C(4; −1);
D. D(−1; 3).
Đáp án: C
Giải thích:
+ Xét điểm A(2; 1) ta có: 22 + 12 – 2.2 + 10.1 + 1 = 12 ≠ 0 nên A ∉ (C)
+ Xét điểm B(3; −2) ta có: 32 + (−2)2 – 2.3 + 10.(−2) + 1 = −12 ≠ 0 nên B ∉ (C)
+ Xét điểm C(4; −1) ta có: 42 + (−1)2 – 2.4 + 10.( −1) + 1 = 0 nên C ∈ (C)
+ Xét điểm D(−1; 3) ta có: (−1)2 + 32 – 2.( −1) + 10.3 + 1 = 43 ≠ 0 nên D ∉ (C)
Câu 6. Giá trị m để đường thẳng ∆: (m – 1)y + mx – 2 = 0 là tiếp tuyến của đường tròn (C): x2 + y2 – 6x + 5 = 0
A. m = 0 hoặc m = 4;
B. m = 0 hoặc m = −4;
C. m = 1 hoặc m = 3;
D. m = 2 hoặc m = −6.
Đáp án: A
Giải thích:
Đường tròn (C) có tâm I(3; 0) và bán kính R = √32+02−5 = 2
Để ∆ là tiếp tuyến của đường tròn (C) thì d(I; ∆) = R
⇔|3m−2|√(m−1)2+m2=2
⇔|3m−2|=2√(m−1)2+m2
⇔9m2−12m+4=4(m2−2m+1+m2)
⇔m2−4m=0
⇔ [m=0m=4.
Câu 7. Cho đường tròn (C): x2 + y2 − (m + 2)x – (m + 4)y + m + 1 = 0. Giá trị của m để đường tròn (C) đi qua điểm A(2; −3)
A. m = −11;
B. m = 11 ;
C. m = 9;
D. m = 2.
Đáp án: A
Giải thích:
Để điểm A thuộc đường tròn (C) thì
22 + (−3)2 – 2.(m + 2) – (− 3)(m + 4) + m + 1 = 0
⇔ 4 + 9 – 2m – 4 + 3m + 12 + m + 1 = 0
⇔ 2m + 22 = 0
⇔ m = −11.
Câu 8. Phương trình tiếp tuyến d của đường tròn (C): (x + 2)2 + (y + 2)2 = 25 tại điểm M(2; 1) là:
A. –y + 1 = 0;
B. 4x + 3y – 11 = 0;
C. 4x + 3y + 14 = 0;
D. 3x – 4y – 2 = 0.
Đáp án: B
Giải thích:
Đường tròn (C) có tâm I(−2; −2)
⇒→IM=(4;3)
Vậy phương trình tiếp tuyến d của đường tròn (C) tại điểm M(2; 1) và có vectơ pháp tuyến →IM=(4;3) là: 4(x – 2) + 3(y – 1) = 0 ⇔ 4x + 3y – 11 = 0.
Câu 9. Cho phương trình x2 + y2 – 2mx – 4(m – 2)y + 6 – m = 0 (1) . Tìm điều kiện của m để (1) là phương trình đường tròn.
A. m ∈ (1; 2);
B. m ∈ (−∞; 1) ∪ (2; +∞);
C. m ∈ (−∞; 1] ∪ [2; +∞);
D. m ∈ [1; 2].
Đáp án: B
Giải thích:
Phương trình (1) có : a = m; b = 2(m – 2); c = 6 – m
Phương trình (1) là phương trình đường tròn khi và chỉ khi a2 + b2 – c > 0
⇔ m 2 + 4(m – 2)2 – (6 – m) > 0
⇔ 5m 2 – 15m + 10 > 0
⇔ m ∈ (−∞; 1) ∪ (2; +∞).
Câu 10. Cho đường tròn (C) có đường kính AB với A(−2; 1), B(4; 1). Khi đó, phương trình đường tròn (C):
A. x2 + y2 + 2x + 2y + 9 = 0;
B. x2 + y2 + 2x + 2y – 7 = 0;
C. x2 + y2 – 2x – 2y – 7 = 0;
D. x2 + y2 – 2x – 2y + 9 = 0.
Đáp án: C
Giải thích:
Ta có tâm I là trung điểm của đường kính AB nên toạ độ điểm I là: {x=−2+42=1y=1+12=1
⇒ I(1; 1)
R = IA = √(1+2)2+(1−1)2 = 3
Vậy phương trình đường tròn là: (x – 1)2 + (y – 1)2 = 9
⇔ x2 + y2 – 2x – 2y – 7 = 0.
III. Vận dụng
Câu 1. Cho đường thẳng d: 2x – y – 5 = 0 và hai điểm A(1; 2) và B(4; 1). Viết phương trình đường tròn (C) có tâm thuộc d và đi qua hai điểm A, B
A. (x + 1)2 + (y + 3)2 = 25;
B. (x – 1)2 + (y – 3)2 = 5;
C. (x – 1)2 + (y + 3)2 = 5;
D. (x – 1)2 + (y + 3)2 = 25.
Đáp án: D
Giải thích:
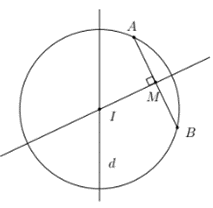
Gọi M là trung điểm của AB nên M(52;32)
⇒ Đường trung trực (∆) của đoạn thẳng AB đi qua tâm I của đường tròn
Mặt khác ta có: ∆ đi qua điểm M và nhận vectơ →AB = (3; – 1) làm vectơ pháp tuyến nên có phương trình là: 3(x – 52) – (y – 32) = 0 ⇔ 3x – y – 6 = 0
Vì I = (∆) ∩ (d) nên toạ độ điểm I thoả mãn hệ ⇔ {2x−y−5=03x−y−6=0
⇒ I(1; -3)
Bán kính R = IA = √(1−1)2+(3+2)2 = 5.
Vậy phương trình đường tròn (C) là: (x – 1)2 + (y + 3)2 = 25.
Câu 2. Phương trình đường tròn đi qua ba điểm M(-2; 4); N(5; 5); P(6; -2) là:
A. x2 + y2 – 4x – 2y – 20 = 0;
B. x2 + y2 – 2x – 2y – 7 = 0;
C. x2 + y2 + 4x – 2y – 14 = 0;
D. x2 + y2 + 2x – 2y + 11 = 0.
Đáp án: A
Giải thích:
Gọi phương trình đường tròn (C) có dạng : x2 + y2 – 2ax – 2by + c = 0
Vì đường tròn (C) đi qua 3 điểm M; N; P nên ta có hệ phương trình:
{4+16+4a−8b+c=025+25−10a−10b+c=036+4−12a+4b+c=0 ⇒ {4a−8b+c=−20−10a−10b+c=−50−12a+4b+c=−40⇒{a=2b=1c=−20
Vậy phương trình đường tròn (C) là: x2 + y2 – 4x – 2y – 20 = 0
Câu 3. Cho tam giác ABC có A(1; 1), B(1; – 3), C(– 5; 9). Bán kính đường tròn nội tiếp tam giác ABC gần với giá trị:
A. 694;
B. 26;
C. 27;
D. 695.
Đáp án: B
Giải thích:
Gọi M và N lần lượt là trung điểm của BC và AB.
Khi đó M( – 2; 3) và N(1; – 1).
Ta có: →AC = (– 6; 8)
Phương trình đường trung trực của đoạn thẳng AC nhận →nAC = (3; – 4) làm vectơ pháp tuyến và đi qua N( 1; – 1) là: 3(x – 1) – 4(y + 1) = 0 ⇔ 3x – 4y – 7 = 0.
Ta có:→BC=(−6; 12)
Phương trình đường trung trực của đoạn thẳng BC nhận →nBC = (1; – 2) làm vectơ pháp tuyến và đi qua M( – 2; 3) là: x + 2 – 2(y – 3) = 0 ⇔ x – 2y + 8 = 0.
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Do đó I là giao điểm của các đường trung trực nên tọa độ điểm I là nghiệm của hệ phương trình:
{x−2y=−83x−4y=7⇔{x=23y=312⇒I(23;312)
⇒ →IA = (– 22; −292) ⇒ IA = √(−22)2+(−292)2=√27774≈26.
Câu 4. Viết phương trình tiếp tuyến ∆ của đường tròn (C) : x2 + y2 – 2x + 4y + 4 = 0 . Biết rằng tiếp tuyến vuông góc với đường thẳng x + 2y + 5 = 0
A. 2x + 5 y + √5−4= 0 và 2x + 5 y −√5−4= 0;
B. 2x – 5 y + √5−4= 0 và 2x – 5 y -√5−4= 0;
C. 2x – 5 y + √5+4 = 0 và 2x – 5 y +√5+4 = 0;
D. 2x – 5 y − √5−4= 0 và 2x – 5 y −√5+4= 0.
Đáp án: B
Giải thích:
Đường tròn (C) có tâm I(1; −2) và bán kính R = 1
Đường thẳng x + 2y + 5 = 0 có vectơ pháp tuyến là →n1(1;2)
Theo giả thiết ta có: đường thẳng ∆ vuông góc với đường thẳng x + 2y + 5 = 0 nên đường thẳng ∆ nhận →n1 làm vectơ chỉ phương. Do đó vectơ pháp tuyến của đường thẳng ∆ là →nΔ(2;−1).
Phương trình đường thẳng ∆ có dạng 2x – y + m = 0
Vì ∆ là tiếp tuyến của (C) nên d(I; ∆) = R
⇔ |2+2+m|√12+22= 1
⇔ |4+m|=√5
⇔ [4+m=√54+m=−√5
⇔ [m=√5−4m=−√5−4
+ Với m = √5−4thì phương trình của ∆ là: 2x – y + √5−4= 0
+ Với m = −√5−4thì phương trình của ∆ là: 2x – y −√5−4= 0
Câu 5. Trong hệ toạ độ Oxy, cho ba đường thẳng d: x − 6y − 10 = 0; d1 : 3x + 4y + 5 = 0 và d2 : 4x – 3y – 5 = 0. Phương trình đường tròn (C) có tâm thuộc d ; và tiếp xúc với 2 đường thẳng d1 và d2 là:
A. (x − 10)2 + y2 = 49;
B. (x+1043)2+(y+7043)2=(743)2;
C. (x − 10)2 + y2 = 49 và (x−1043)2+(y+7043)2=(743)2;
D. (x + 10)2 + y2 = 49 và (x+1043)2+(y+7043)2=(743)2.
Đáp án: C
Giải thích:
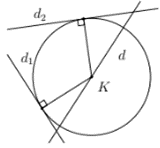
Gọi I là tâm của đường tròn (C)
Vì I ∈ d nên I(6t + 10; t)
Theo giả thiết ta có: d (I; d1) = d (I; d2) = R
⇔ |3.(6t+10)+4t+5|√32+42 = |4.(6t+10)−3t−5|√42+(−3)2
⇔ |22t+35|=|21t+35|
⇒[22t+35=21t+3522t+35=−21t−35
⇔ [22t−21t=35−3522t+21t=−35−35
⇔ [t=0t=−7043
+ Với t = 0 thì I (10; 0) và R = 7.
Do đó phương trình đường tròn (C) là: (x − 10)2 + y2 = 49
+ Với t = −7043 thì I(1043;−7043) và R = 743.
Do đó phương trình đường tròn (C) là: (x−1043)2+(y+7043)2=(743)2.