50 câu Trắc nghiệm Ôn tập Chương 3 (có đáp án 2024) – Toán 10 Kết nối tri thức
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Ôn tập Chương 3: Hệ thức lượng trong tam giác đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Chương 3.
Trắc nghiệm Toán 10 Ôn tập Chương 3
I. Nhận biết
Câu 1. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Khẳng định nào dưới đây đúng?
A. a2 = b2 + c2 + 2bcsinA;
B. a2 = b2 + c2 – 2bccosA;
C. a2 = b2 + c2 – 2acsinA;
D. a2 = b2 + c2 + 2abcosA.
Đáp án: B
Giải thích:
Định lí côsin:
Trong tam giác ABC: a2 = b2 + c2 – 2bccosA.
Vậy đáp án đúng là B.
Câu 2. Khẳng định nào sau đây đúng ?
A. sin45° = ;
B. cos45° = 1;
C. tan45° = 1;
D. cot45° = .
Đáp án: C
Giải thích:
Sử dụng máy tính cầm tay ta tính được:
sin45° = ; cos45° = ; tan45° = 1; cot45° = 1.
Do đó A, B, D sai và C đúng.
Câu 3. Khẳng định nào sau đây đúng ?
A. ;
B. ;
C. ;
D. .
Đáp án: A
Giải thích:
Giả sử = x.
Ta có cosx = ; sinx = .
.
Câu 4. Cho tam giác ABC. Công thức nào sau đây sai?
A. ;
B. ;
C. ;
D. .
Đáp án: D
Giải thích:
Định lí sin: Trong tam giác ABC
.
Khẳng định A, B, C đúng. Khẳng định D sai.
Vậy chọn đáp án D.
Câu 5. Nội dung nào thể hiện công thức Heron?
A. S = ;
B. S = ;
C. S = ;
D. S = .
Đáp án: D
Giải thích:
Công thức Heron: S = .
Câu 6. Khẳng định nào sau đây đúng ?
A. sin( 180° – α ) = – sinα;
B. cos( 180° – α ) = cosα;
C. sin( 90° – α ) = – cosα;
D. cos( 90° – α ) = sinα.
Đáp án: D
Giải thích:
Hai góc bù nhau có sin bằng nhau, côsin, tang, côtang đối nhau.
Khi đó ta có:
sin( 180° – α ) = sinα;
cos( 180° – α ) = – cosα.
Do đó A và B sai.
Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Khi đó ta có:
sin( 90° – α ) = cosα;
cos( 90° – α ) = sinα.
Do đó C sai và D đúng.
Câu 7. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Nội dung nào thể hiện định lí côsin?
A. ;
B. a2 = b2 + c2 – 2bccosA;
C. S = bcsinA = acsinB = absinC;
D. b2 = a2 + c2 – 2bccosB .
Đáp án: B
Giải thích:
Định lí côsin: Trong tam giác ABC
a2 = b2 + c2 – 2bccosA
b2 = a2 + c2 – 2accosB
c2 = b2 + a2 – 2bacosC.
Vậy đáp án đúng là B.
Câu 8. M là điểm trên nửa đường trong lượng giác sao cho = α. Tọa độ của điểm M là:
A. (sin α; cos α);
B. (cos α; sin α);
C. (– sin α; cos α);
D. ( – cos α; – sin α).
Đáp án: B
Giải thích:
Định nghĩa tỉ số lượng giác của 1 góc bất kì từ 0° đến 180°:
Với góc α cho trước, 0° ≤ α ≤ 180°.
Gọi M(x0;y0) là điểm trên nửa đường tròn đơn vị nói trên sao cho = α. Ta có:
+ Sin của góc α là tung độ y0 của điểm M kí hiệu là sinα.
+ Côsin của góc α là hoành độ x0 của điểm M kí hiệu là cosα.
Câu 9. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Công thức tính diện tích nào dưới đây đúng?
A. S = bcsinA;
B. S = absinB;
C. S = 2acsinB;
D. S = 2bcsinA.
Đáp án: A
Giải thích:
Công thức tính diện tích tam giác ABC: S = bcsinA.
Câu 10. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Nội dung nào thể hiện định lí sin?
A. ;
B. a2 = b2 + c2 – 2bccosA;
C. S = bcsinA = acsinB = absinC;
D. b2 = a2 + c2 – 2accosB .
Đáp án: B
Định lí côsin: Trong tam giác ABC
a2 = b2 + c2 – 2bccosA
b2 = a2 + c2 – 2accosB
c2 = b2 + a2 – 2bacosC.
Vậy đáp án đúng là B.
II. Thông hiểu
Câu 1. Cho tam giác ABC có a = 2, b = 5, c = 5. Tính bán kính đường tròn nội tiếp tam giác ABC.
A. 1;
B. ;
C. 0,5;
D. .
Đáp án: D
Giải thích:
Ta có: p = = 6
Áp dụng công thức Heron:
S = .
S =
S = .
Mà S = pr = 6r = ⇒ r = .
Vậy đáp án đúng là D.
Câu 2. Tính giá trị biểu thức S = sin235° + cos225° + sin255° + cos265°.
A. 3;
B. 2;
C. 1;
D. 0.
Đáp án: B
Giải thích:
Sử dụng: sin( 90° – α ) = cosα và cos( 90° – α ) = sinα
S = sin235° + cos225° + sin255° + cos265°
⇔ S = sin235° + cos225° + [ sin(90° – 35°)]2 + [ cos(90° – 25°)]2
⇔ S = sin235° + cos225° + cos235° + sin225°
⇔ S = ( sin235° + cos235° ) + ( cos225° + sin225° )
⇔ S = 2.
Câu 3. Tính diện tích tam giác ABC có b = 2, = 30°, = 45°.
A. 1 + ;
B. 1 – ;
C. ;
D. .
Đáp án: A
Giải thích:
Xét tam giác ABC có: + + = 180° ⇒ = 180° – 30° – 45° = 105°.
Áp dụng định lí sin: ⇒ ⇒ c = .
S = bcsinA = .2..sin105° = 1 +
Vậy đáp án A đúng.
Câu 4. Biểu thức P = tan15°.tan25°.tan35°.tan55°.tan65°.tan75° có giá trị bằng?
A. 2;
B. –1;
C. 1;
D. 0.
Đáp án: C
Giải thích:
Sử dụng công thức: tan( 90° – α ) = cotα và hay tanα.cotα = 1
P = tan15°.tan25°.tan35°.tan55°.tan65°.tan75°
⇔ P = tan15°.tan25°.tan35°.cot35°.cot25°.cot15°
⇔ P = (tan15°.cot15°)(tan25°.cot25°).(tan35°.cot35°)
⇔ P = 1.1.1
⇔ P = 1.
Câu 5. Tính giá trị biểu thức P = sin30°.cos15° + sin150°.cos165°
A. 0;
B. 1;
C. – 1;
D. 0,5.
Đáp án: A
Giải thích:
Sử dụng công thức: sin( 180° – α ) = sinα và cos( 180° – α ) = – cosα.
Có sin30° = sin150°; cos15° = – cos165°
P = sin30°.cos15° – sin30°.cos15°= 0.
Câu 6. Tam giác ABC có AB = , BC = , CA = . Tính số đo góc A.
A. 60°;
B. 90°;
C. 120°;
D. 30°.
Đáp án: C
Giải thích:
Đặt AB = c, BC = a, AC = b
Theo định lí côsin ta có: a2 = b2 + c2 – 2bccosA
⇒ cosA =
⇒ cosA =
⇒ cosA =
⇒ = 120°.
Vậy đáp án C đúng.
Câu 7. Cho tam giác ABC có BC = 8 và = 30°. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
A. ;
B. ;
C. 16;
D. 8.
Đáp án: D
Giải thích:
Áp dụng định lí sin trong tam giác ABC:
= 2R
R =
R =
R = 8.
Vậy đáp án đúng là D.
Câu 8. Cho tam giác ABC. Tính P = sinA.cos(B + C) + sin(B + C).cosA
A. 0;
B. 1;
C. -1;
D. 0,5.
Đáp án: A
Giải thích:
Giả sử: = α; . Do , là 3 góc trong tam giác nên α + β = 180°
⇒ β = 180° – α
⇒ sinβ = sin(180° – α) = sinα và cosβ = cos( 180° – α ) = – cosα
P = sinA.cos(B + C) + sin(B + C).cosA = sinα.cosβ + sinβ.cos α = sinα.(–cosα) + sinα.cos α = 0.
Câu 9. Cho tam giác ABC có b = 8, c = 5 và = 80°. Tính số đo góc C.
A. 37°98’;
B. 38°98’;
C. 37°59’;
D. 36°98’.
Đáp án: C
Giải thích:
Áp dụng định lí sin:
⇒
⇒ sin C = 5 :
⇒ ≈ 37°59’
Vậy đáp án đúng là C.
Câu 10. Cho tam giác ABC có a = 3, b = 4, c = 5. Tính diện tích tam giác ABC.
A. ;
B. 6;
C. 12;
D. 8.
Đáp án: B
Giải thích:
Ta có: p = = 6
Áp dụng công thức Heron:
S = .
S =
S = 6.
Vậy đáp án đúng là B.
Câu 11. Cho tam giác ABC có = 120°, AB = 6, BC = 7. Tính AC.
A. ;
B. ;
C. 8;
D. .
Đáp án: A
Giải thích:
Áp dụng định lí côsin trong tam giác ABC:
AC2 = AB2 + BC2 – 2AB.BC.cosB
AC2 = 62 + 72 – 2.6.7.cos120°
AC2 = 127
AC =
Vậy đáp án A đúng.
Câu 12. Cho P = ( sinα + cosβ)(sinα − cosβ) + (cosα + sinβ)(cosα − sinβ)
Giá trị của biểu thức P là?
A. 1;
B. 0;
C. 2;
D. 3.
Đáp án: B
Giải thích:
P = ( sinα + cosβ)(sinα − cosβ) + (cosα + sinβ)(cosα − sinβ)
⇔ P =
⇔ P = 0
Câu 13. Tính giá trị biểu thức A = cot20° + cot40° + cot60° + .... + cot160°
A. 1;
B. 2;
C. 0;
D. 4.
Đáp án: C
Giải thích:
Sử dụng cot( 180° – α ) = – cotα với 0° < α < 180°
Hay cot( 180° – α ) + cotα = 0
A = ( cot20° + cot160°) + ( cot40° + cot140°) + ( cot60° + cot120°) + ( cot80° + cot100°)
⇔ A = 0.
Câu 14. Cho tam giác ABC có AB = 5, AC = 6, BC = 7. Tính cosB.
A. ;
B. ;
C. ;
D. .
Đáp án: C
Giải thích:
Áp dụng định lí côsin trong tam giác ABC, có:
AC2 = AB2 + BC2 – 2AB.BC.cosB
62 = 52 + 72 – 2.5.7.cosB
cosB =
cosB =
Vậy đáp án đúng là C.
Câu 15. Cho góc α biết sinα + cosα = . Tính A = sinα.cosα
A. ;
B. ;
C. ;
D. .
Đáp án: A
Giải thích:
⇔ .
III. Vận dụng
Câu 1. Cho 3cosα – sinα = 1; 0° < α < 90°. Tính tanα.
A. ;
B. ;
C. ;
D. .
Đáp án: A
Giải thích:
3cosα – sinα = 1
⇔ 3cosα = 1 + sinα
⇒ 9cos2α = (sinα + 1)2 = sin2α + 2.sin α +1
⇒ 9 – 9sin2 α = sin2α + 2.sin α +1
⇒ 10 sin2α + 2.sinα – 8 = 0
⇒ sinα = – 1 hoặc sinα =
Với sinα = – 1 không thỏa mãn
Với sinα = ⇒ cosα =
Vậy tanα = .
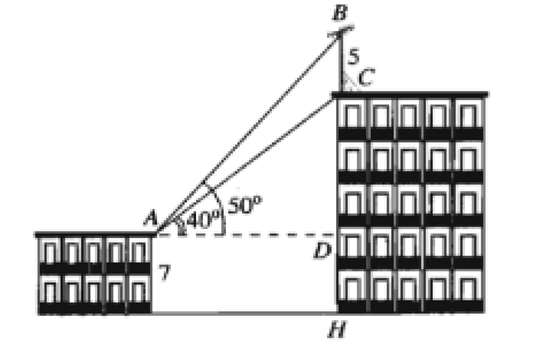
Câu 2. Trên nóc tòa nhà có một cột ăng – ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
A. 12m;
B. 19m;
C. 29m;
D. 24m.
Đáp án: B
Giải thích:
Gọi điểm H là chân tòa nhà. Điểm D là điểm tương ứng trên tòa nhà ngang bằng với vị trí quan sát A. Như vậy = 90°.
Từ vị trí quan sát A cao 7m so với mặt đất có thể quan sát được đỉnh B và chân C của cột ăng – ten dưới góc 50° và 40° so với phường nằm ngang. Như vậy = 40° và = 50°.
Xét tam giác ABD có: = 180 – – = 180° – 90° – 50° = 40° = .
Xét tam giác ABC có:
= 50° – 40° = 10°.
Áp dụng định lí sin cho tam giác ABC:
⇒ ⇒ AC ≈ 18,5m
Áp dụng định lí sin cho tam giác ADC:
⇒ ⇒ CD ≈ 11,9m
Chiều cao tòa nhà tương ứng với đoạn CH.
CH = CD + DH = 11,9 + 7 = 18,9 ≈ 19m.
Vậy đáp án đúng là B.
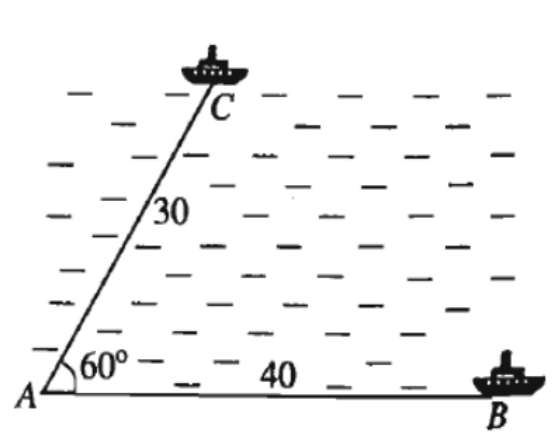
Câu 3. Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu tới B chạy với tốc độ 20 hải lí một giờ. Tàu tới C chạy với tốc độ 15 hải lí một giờ. Hỏi sau hai giờ hai tàu cách nhau bao nhiêu hải lí? ( Chọn kết quả gần nhất ).
A. 61 hải lí;
B. 36 hải lí;
C. 18 hải lí;
D. 21 hải lí.
Đáp án: B
Giải thích:
Sau 2h, tàu tới C đi được đoạn đường b = 15.2 = 30 ( hải lí )
Sau 2h, tàu tới B đi được đoạn đường c = 15.2 = 40 ( hải lí )
Dựa vào hình vẽ, sau 2h, tàu B và tàu C tạo với điểm xuất phát một tam giác ABC có
= 60°, b = 30, c = 40 và a = BC.
Áp dụng định lí côsin ta có:
a2 = b2 + c2 – 2bccosA
a2 = 302 + 402 – 2.30.40.cos60°
a2 = 1300
a ≈ 36 ( hải lí ).
Vậy đáp án đúng là B.
Câu 4. Tam giác ABC có BC = a, AC = b, AB = c. Các cạnh a, b, c liên hệ với nhau bằng đẳng thức b.( b2 – a2 ) = c.( a2 – c2 ). Tính .
A. 120°;
B. 90°;
C. 30°;
D. 60°.
Đáp án: D
Giải thích:
b.( b2 – a2 ) = c.( a2 – c2 )
⟺ b3 – a2b – a2c + c3 = 0
⟺ b3 + c3 – ( a2b + a2c ) = 0
⟺ ( b + c )( b2 – bc + c2 ) – a2( b + c ) = 0
⟺ ( b + c ) ( b2 + c2 – a2 – bc ) = 0
b và c là cạnh tam giác nên b + c > 0
⇒ b2 + c2 – a2 – bc = 0 hay a2 = b2 + c2 – bc
Theo định lí côsin
a2 = b2 + c2 – 2bccosA
mà a2 = b2 + c2 – bc ⇒ cosA = ⇒ = 60°.
Vậy đáp án đúng là D.
Câu 5. Cho biết . Tính cotα biết 0° < α < 90°.
A. ;
B. ;
C. ;
D. .
Đáp án: C
Giải thích:
2cosα + sinα = 2 ⟺ sinα = 2 – 2cosα ⇒ 2sin2α = 4 – 8cos + 4 cos2α
⟹ 2 – 2cos2α = 4 – 8cosα + 4cos2α
⟹ 6cos2 α – 8cosα + 2 = 0
cosα = 1 không thỏa mãn 0° < α < 90°.
cosα = ⇒ cotα= .