Lý thuyết Mẫu số liệu ghép nhóm (Kết nối tri thức 2024) Toán 11

Lý thuyết Toán lớp 11 Bài 8: Mẫu số liệu ghép nhóm

Bài giảng Toán 11 Bài 8: Mẫu số liệu ghép nhóm

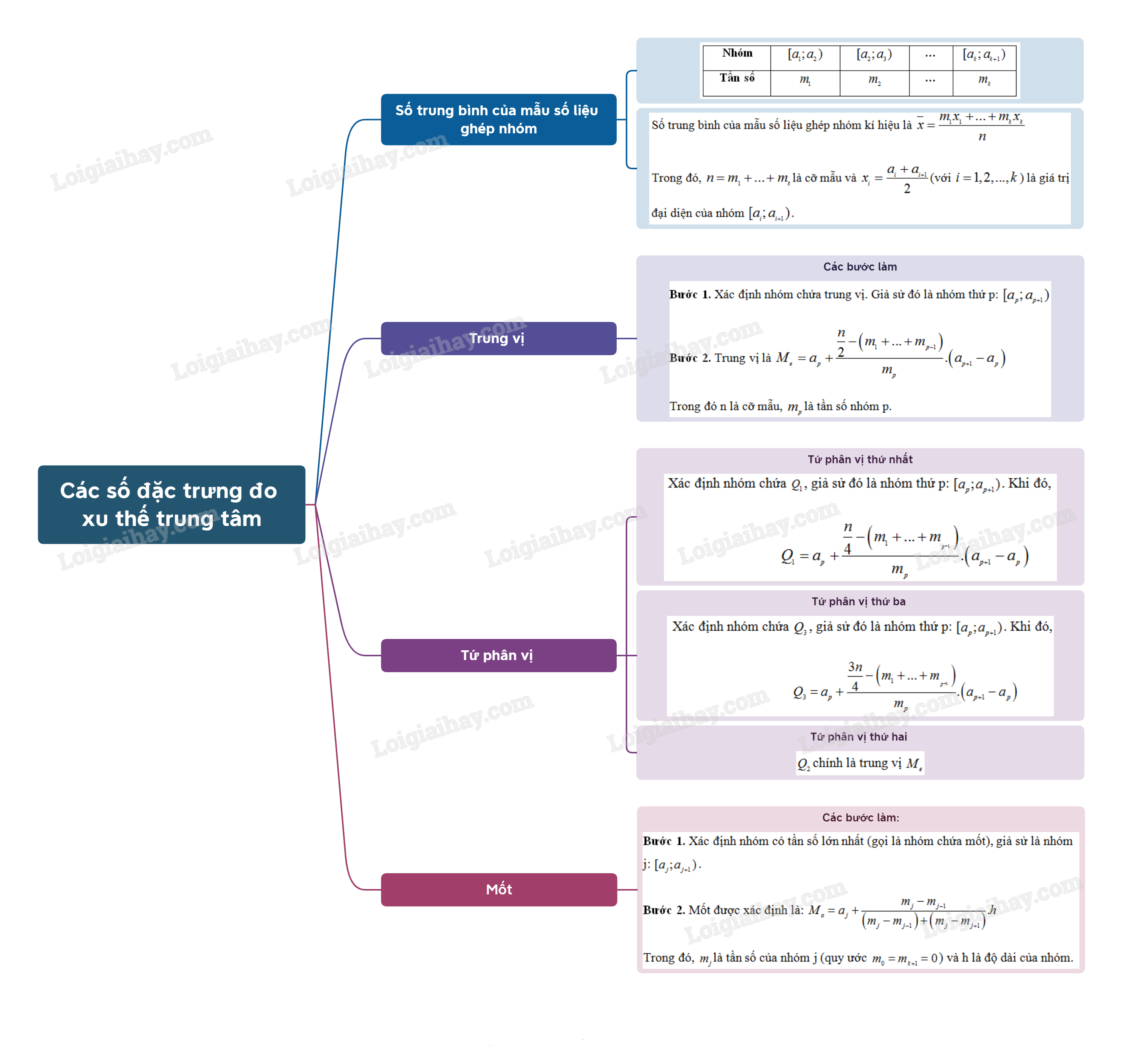
A. Lý thuyết Các số đặc trưng đo xu thế trung tâm

1. Số trung bình của mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là $\overline{x}=\frac{m_1{x}_1+...+m_k{x}_k}{n}$

Trong đó, $n=m_1+...+m_k$ là cỡ mẫu và $x_i=\frac{a_i+a_{i+1}}{2}$(với $i=1,2,...,k$) là giá trị đại diện của nhóm $[a_i;a_{i+1})$.

2. Trung vị của mẫu số liệu ghép nhóm

Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:

Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: $[a_p;a_{p+1})$.

Bước 2. Trung vị là $M_e=a_p+\frac{\frac{n}{2}-\left(m_1+...+m_{p-1}\right)}{m_p}.\left(a_{p+1}-a_p\right)$

Trong đó n là cỡ mẫu, $m_p$ là tần số nhóm p.

Với $p=1$, ta quy ước $m_1+...+m_{p-1}=0$

3. Tứ phân vị của mấu số liệu ghép nhóm

Để tính tứ phân vị thứ nhất $Q_1$ của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa $Q_1$, giả sử đó là nhóm thứ p: $[a_p;a_{p+1})$. Khi đó,

$Q_1=a_p+\frac{\frac{n}{4}-\left(m_1+...+m_{{}_{p-1}}\right)}{m_p}.\left(a_{p+1}-a_p\right)$

Trong đó n là cỡ mẫu, $m_p$ là tần số nhóm p.

Với $p=1$, ta quy ước $m_1+...+m_{p-1}=0$

Để tính tứ phân vị thứ ba $Q_3$ của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa $Q_3$, giả sử đó là nhóm thứ p: $[a_p;a_{p+1})$. Khi đó,

$Q_3=a_p+\frac{\frac{3n}{4}-\left(m_1+...+m_{{}_{p-1}}\right)}{m_p}.\left(a_{p+1}-a_p\right)$

Trong đó n là cỡ mẫu, $m_p$ là tần số nhóm p. Với $p=1$, ta quy ước $m_1+...+m_{p-1}=0$

Tứ phân vị thứ hai $Q_2$ chính là trung vị $M_e$.

4. Mốt của mẫu số liệu ghép nhóm

Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:

Bước 1. Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: $[a_j;a_{j+1})$.

Bước 2. Mốt được xác định là: $M_o=a_j+\frac{m_j-m_{j-1}}{\left(m_j-m_{j-1}\right)+\left(m_j-m_{j+1}\right)}.h$

Trong đó, $m_j$ là tần số của nhóm j (quy ước $m_0=m_{k+1}=0$) và h là độ dài của nhóm.

• Lưu ý:

Người ta chỉ định nghĩa mốt cho mẫu ghép nhóm có độ dài các nhóm bằng nhau. Một mẫu có thể không có mốt hoặc có nhiều hơn một mốt.

• Ý nghĩa:

Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc, nó được dùng để đo xu thế trung tâm của mẫu số liệu.

B. Bài tập Các số đặc trưng đo xu thế trung tâm

Bài 1: Cho bảng số liệu khảo sát về tuổi thọ (đơn vị: nghìn giờ) của một loại bóng đèn:

a) Mẫu số liệu đã cho có là mẫu số liệu ghép nhóm hay không?

b) Có bao nhiêu bóng đèn được khảo sát và bao nhiêu bóng đèn có tuổi thọ từ 9 nghìn giờ trở lên?

Hướng dẫn giải

a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm.

b) Số bóng đèn được khảo sát là 4 + 20 + 26 + 42 + 8 = 100.

Số bóng đèn có tuổi thọ từ 9 nghìn giờ trở lên là 42 + 8 = 50.

Bài 2: Cho mẫu số liệu về chiều cao của các học sinh lớp 11B (đơn vị: cm)

Hãy chuyển mẫu số liệu trên thành mẫu số liệu ghép nhóm gồm năm nhóm có độ dài bằng nhau.

Hướng dẫn giải

Giá trị nhỏ nhất của mẫu là 156; giá trị lớn nhất là 173 nên khoảng biến thiên là 173 – 156 = 17.

Ta cần mẫu số liệu thành 5 nhóm.

Để thuận tiện ta chọn đầu mút trái của nhóm đầu tiên là 156 và đầu mút phải của nhóm cuối cùng là 173,5; độ dài mỗi nhóm là 3,5 ta được các nhóm là [156;159,5), [159,5; 163), [163; 166,5), [166,5;170), [170; 173,5).

Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau: