Lý thuyết : Dãy số (Kết nối tri thức 2024) Toán 11

Lý thuyết Toán 11 Bài 5: Dãy số - Kết nối tri thức

Bài giảng Toán 11 Bài 5: Dãy số

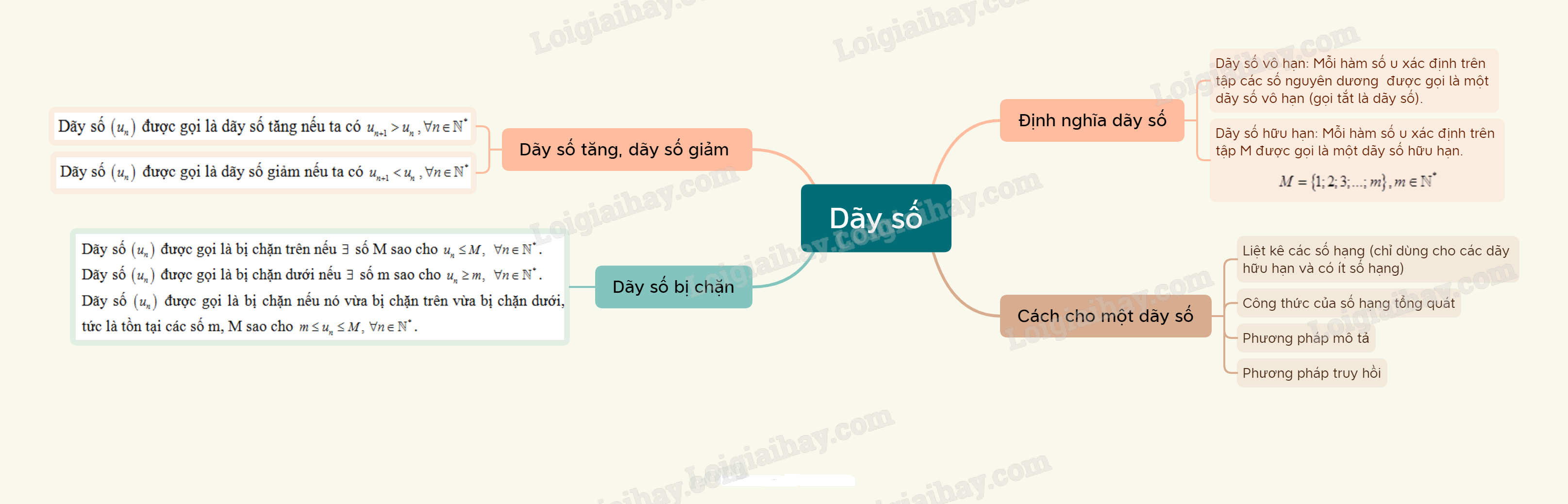
A. Lý thuyết Dãy số

1. Định nghĩa dãy số

• Dãy số vô hạn

Mỗi hàm số u xác định trên tập các số nguyên dương ${\mathbb{N}}^{\ast }$được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu là $u=u\left(n\right)$.

Ta thường viết $u_n$thay cho $u\left(n\right)$ và kí hiệu dãy số $u=u\left(n\right)$bởi $u\left(n\right)$, do đó dãy số $\left(u_n\right)$được viết dưới dạng khai triển $u_1,u_2,u_3,...,u_n,...$

Số $u_1$ là số hạng đầu; $u_n$là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

*Chú ý: Nếu $\mathrm{\forall }n\in {\mathbb{N}}^{\ast },u_n=c$thì $\left(u_n\right)$được gọi là dãy số không đổi.

• Dãy số hữu hạn

Mỗi hàm số u xác định trên tập $M=\left\{1;2;3;...;m\right\},m\in {\mathbb{N}}^{\ast }$ được gọi là một dãy số hữu hạn.

Dạng khai triển của dãy số hữu hạn là $u_1,u_2,u_3,...,u_m$.

Số $u_1$ gọi là số hạng đầu, $u_m$là số hạng cuối.

2. Cách cho một dãy số

Một dãy số có thể cho bằng:

+) Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).

+) Công thức của số hạng tổng quát.

+) Phương pháp mô tả.

+) Phương pháp truy hồi.

3. Dãy số tăng, dãy số giảm và dãy số bị chặn

Dãy số $\left(u_n\right)$ được gọi là dãy số tăng nếu ta có $u_{n+1}>u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là dãy số giảm nếu ta có $u_{n+1}<u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn trên nếu $\mathrm{\exists }$ số M sao cho $u_n\le M,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn dưới nếu $\mathrm{\exists }$ số m sao cho $u_n\ge m,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho $m\le u_n\le M,$$\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

B. Bài tập Dãy số

Bài 1: Dãy số (un) cho bởi hệ thức truy hồi: u1 = 1, u­n = n . un-1 với n ≥ 2.

a) Viết năm số hạng đầu của dãy số.

b) Dự đoán công thức số hạng tổng quát un.

Hướng dẫn giải

a) Năm số hạng đầu của dãy số là: 1, 2, 6, 24, 120.

b) Ta thấy u1 =1!, u2 = 2!, u3 = 3!, u4 = 4!, u5 = 5!.

Vậy công thức số hạng tổng quát là un = n!.

Bài 2: Viết số hạng tổng quát của dãy số tăng gồm tất cả các số nguyên dương mà mỗi số hạng của nó:

a) Đều chia hết cho 2;

b) Khi chia cho 3 dư 1.

Hướng dẫn giải

a) un = 2n (∀n ∈ ℕ*).

b) un = 3n + 1 (∀n ∈ ℕ*).

Bài 3: Xét tính tăng, giảm của dãy số (un), biết:

a) un = 3n – 1;

b) un = – 3n + 1.

Hướng dẫn giải

a) Ta có: un+1 – un = [3(n + 1) – 1] – (3n – 1) = (3n + 2) – 3n + 1 = 3 > 0, tức là un+1 > un

Suy ra đây là dãy số tăng.

b) Ta có: un+1 – un = [–3(n + 1) + 1] – (–3n + 1) = (–3n – 2) + 3n – 1 = – 3 < 0, tức là un+1 < un.

Suy ra đây là dãy số giảm.

Bài 4: Trong các dãy số (un) sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn?

a) un = 2n – 1;

b) un = $\frac{2n+2}{2n+3}$;

c) un = cos n.

Hướng dẫn giải

a) un = 2n – 1 ≥ 1 với ∀n ∈ ℕ*

Vậy dãy số (un) bị chặn dưới.

b) Dãy số (un) bị chặn trên, vì $u_n=\frac{2n+2}{2n+3}=\frac{2n+3-1}{2n+3}=1-\frac{1}{2n+3}<1$, ∀n ∈ ℕ*.

Dãy số (un) bị chặn dưới, vì $u_n=\frac{2n+2}{2n+3}\ge 0$, ∀n ∈ ℕ*.

Vậy dãy số (un) bị chặn.

c) Ta có: −1 ≤ cos n ≤ 1 ∀n ∈ ℕ*.

Vậy dãy số (un) bị chặn.

Hướng dẫn giải

a) un = 2n – 1 ≥ 1 với ∀n ∈ ℕ*

Vậy dãy số (un) bị chặn dưới.

b) Dãy số (un) bị chặn trên, vì $u_n=\frac{2n+2}{2n+3}=\frac{2n+3-1}{2n+3}=1-\frac{1}{2n+3}<1$${\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:11px;"><span\; style="line-height:2;">=</span></span>\frac{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}}{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">3</span></span>}}<span\; style="font-size:11px;"><span\; style="line-height:2;">=</span></span>\frac{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">3</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">1</span></span>}}{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">3</span></span>}}<span\; style="font-size:11px;"><span\; style="line-height:2;">=</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">1</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">-</span></span>\frac{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">1</span></span>}}{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">3</span></span>}}<span\; style="font-size:11px;"><span\; style="line-height:2;"><</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">1</span></span>}$, ∀n ∈ ℕ*.

Dãy số (un) bị chặn dưới, vì $u_n=\frac{2n+2}{2n+3}\ge 0$${\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:11px;"><span\; style="line-height:2;">=</span></span>\frac{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}}{\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">2</span></span>}\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:11px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">3</span></span>}}<span\; style="font-size:11px;"><span\; style="line-height:2;">\ge </span></span>\mathrm{<span\; style="font-size:11px;"><span\; style="line-height:2;">0</span></span>}$, ∀n ∈ ℕ*.

Vậy dãy số (un) bị chặn.

c) Ta có: −1 ≤ cos n ≤ 1 ∀n ∈ ℕ*.

Vậy dãy số (un) bị chặn.

Bài 5: Ông An gửi tiết kiệm 50 triệu đồng kì hạn 1 tháng với lãi suất 7% một năm theo hình thức tính lãi kép. Số tiền (triệu đồng) của ông An thu được sau n tháng được cho bởi công thức

$A_n$= 50.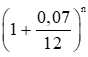

a) Tìm số tiền ông An nhận được sau tháng thứ nhất, sau tháng thứ hai.

b) Tìm số tiền ông An nhận được sau 1 năm.

Hướng dẫn giải

a) Số tiền ông An nhận được sau tháng thứ nhất là:

$A_1$= 50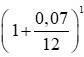 = 50,2917 (triệu đồng).

Số tiền ông An nhận được sau tháng thứ hai là:

$A_2$= 50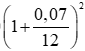 = 50,585 (triệu đồng).

b) 1 năm = 12 tháng

Số tiền ông An nhận được sau 1 năm là:

$A_{12}$= 50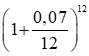 = 53,6145 (triệu đồng).

Bài 6: Viết năm số hạng đầu và số hạng thứ 100 của các dãy số (un) có số hạng tổng quát cho bởi:

a) u­n = 4n – 2;

b) un = 3 . 2n + 1.

Hướng dẫn giải

a) Năm số hạng đầu của dãy số là: 2, 6, 10, 14, 18.

Số hạng thứ 100 của dãy số là: u­100 = 4.100 – 2 = 398.

b) Năm số hạng đầu của dãy số là: 7, 13, 25, 49, 97.

Số hạng thứ 100 của dãy số là: u100 = 3 . 2100 + 1.