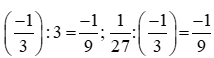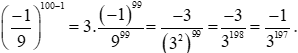Lý thuyết Cấp số nhân (Kết nối tri thức 2024) Toán 11

A. Lý thuyết Cấp số nhân

1. Định nghĩa

Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

Cấp số nhân $\left(u_n\right)$$<span\; style="font-size:10px;"><span\; style="line-height:2;">(</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">)</span></span>$với công bội q được cho bởi hệ thức truy hồi

$u_n=u_{n-1}.q,n\in N^{\ast }$${\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">,</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span>{\mathbb{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}^{<span\; style="font-size:10px;"><span\; style="line-height:2;">\ast </span></span>}$

* Chú ý: Dãy $\left(u_n\right)$$<span\; style="font-size:10px;"><span\; style="line-height:2;">(</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">)</span></span>$ là cấp số nhân thì ${u_k}^2=u_{k-1}.u_{k+1}\left(k\ge 2\right)$${{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}}^{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">2</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">+</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">(</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">\ge </span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">2</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">)</span></span>$.

2. Số hạng tổng quát

Nếu một cấp số nhân có số hạng đầu $u_1$${\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}$ và công bội q thì số hạng tổng quát $u_n$${\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}$của nó được xác định bởi công thức

$u_n=u_1.q^{n-1},n\ge 2$${\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}^{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">,</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">\ge </span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">2</span></span>}$

3. Tổng của n số hạng đầu của một cấp số nhân

Cho cấp số nhân $\left(u_n\right)$$<span\; style="font-size:10px;"><span\; style="line-height:2;">(</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">)</span></span>$với công bội $q\ne 1$$\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">\ne </span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}$. Đặt $S_n=u_1+u_2+u_3+...+u_n$${\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">+</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">2</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">+</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">3</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">+</span></span><span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span><span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span><span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span><span\; style="font-size:10px;"><span\; style="line-height:2;">+</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}$. Khi đó

$S_n=\frac{u_1\left(1-q^n\right)}{1-q}$${\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>\frac{{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">(</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}^{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">)</span></span>}{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}$

B. Bài tập Cấp số nhân

Bài 1: Một cấp số nhân có số hạng đầu bằng 4 và công bội bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số nhân này để có tổng bằng 131 068?

Hướng dẫn giải

Số hạng tổng quát của cấp số nhân là: un = 4 . 2n–1.

Gọi n là số các số hạng cần lấy tổng, ta có

131 068 = Sn = 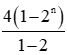 = 4 . 2n – 4

Suy ra: 2n = 32768 = 215, do đó n = 15.

Vậy ta phải lấy 15 số hạng đầu của cấp số nhân.

Bài 2: Viết năm số hạng đầu của dãy số (un) sau và xem nó có phải là cấp số nhân không. Nếu nó là cấp số nhân, hãy tìm công bội q và viết công thức số hạng tổng quát của nó dưới dạng un = u1 . qn–1.

a) un = 4n;

b) un = 3n;

c) u1 = 2, un = nun–1.

Hướng dẫn giải

a) Năm số hạng đầu của dãy là: 4, 8, 12, 16, 20

Ta có: 8 : 4 = 2 ≠ 12 : 8 = $\frac{3}{2}$$\frac{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">3</span></span>}}{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">2</span></span>}}$ nên (un) không phải là cấp số nhân.

b) Năm số hạng đầu của dãy là: 3; 9; 27; 81; 243

Ta có: $\frac{u_n}{u_{n-1}}=\frac{3^n}{3^{n-1}}=3$$\frac{{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}}{{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}_{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>\frac{{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">3</span></span>}}^{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}}}{{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">3</span></span>}}^{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span>}<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}}<span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">3</span></span>}$ với mọi n ≥ 2

Suy ra dãy số là cấp số nhân với u1 = 3 và công bội q = 3.

Số hạng tổng quát: un = 3 . 3n–1.

c) Năm số hạng đầu của dãy là: 2; 4; 12; 48; 240

Ta có: 4 : 2 = 2 ≠ 12 : 4 = 3 nên (un) không phải là cấp số nhân.

Bài 3: Một cấp số nhân có số hạng thứ 6 bằng 10 240 và số hạng thứ 3 bằng 160. Tìm số hạng thứ 50 của cấp số nhân này.

Hướng dẫn giải

Giả sử u1 là số hạng đầu và q là công bội của cấp số nhân đó. Ta có:

u6 = u1 . q5 = 10 240 (1)

u3 = u1 . q2 = 160 (2)

Lấy (1) chia vế theo vế (2) ta được: q3 = 64. Suy ra q = 4.

Với q = 4, ta tính được u­1 = 10.

Suy ra công thức số hạng tổng quát của cấp số nhân là: un = 10 . 4n–1

Vậy số hạng thứ 50 của cấp số nhân này là u50 = 10 . 450–1 = 10 . 449.

Bài 4: Xác định công bội, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số nhân sau:

a) 1, 3, 9, ...;

b) 3, $\frac{-1}{3},\frac{1}{27}$$\frac{<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">3</span></span>}}<span\; style="font-size:10px;"><span\; style="line-height:2;">,</span></span>\frac{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">27</span></span>}}$, ….

Hướng dẫn giải

a) Ta thấy: 3 : 1 = 3, 9 : 3 = 3

Suy ra công bội q = 3

Số hạng tổng quát của cấp số nhân là: un = 3n–1.

Số hạng thứ 5: u5 = 35–1 = 81.

Số hạng thứ 100: u100 = 3100–1 = 399.

b) Ta thấy:

Suy ra cấp số nhân có công bội q = $\frac{-1}{9}$$\frac{<span\; style="font-size:10px;"><span\; style="line-height:2;">-</span></span>\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">9</span></span>}}$.

Số hạng tổng quát của cấp số nhân là: un = 3..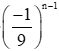

Số hạng thứ 5: u5 = 3.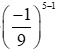= $\frac{1}{2187}$$\frac{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">1</span></span>}}{\mathrm{<span\; style="font-size:10px;"><span\; style="line-height:2;">2187</span></span>}}$.

Số hạng thứ 100: u100 =3.