Lý thuyết Định nghĩa và ý nghĩa của đạo hàm (Kết nối tri thức 2024) Toán 11

Lý thuyết Toán 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm - Kết nối tri thức

A. Lý thuyết Định nghĩa và ý nghĩa của đạo hàm

1. Đạo hàm của hàm số tại một điểm

- Định nghĩa: Cho hàm số y = f(x) xác định trên khoảng $\left(a;b\right)$ và điểm $x_0\in \left(a;b\right)$. Nếu tồn tại giới hạn (hữu hạn)

$\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm $x_0$, kí hiệu là $f^{\prime }\left(x_0\right)$ hoặc $y^{\prime }\left(x_0\right)$.

- Cách viết khác của định nghĩa:

$f^{\prime }\left(x_0\right)=\underset{h\to 0}{lim}\frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}$.

- Quy tắc tính đọa hàm của hàm số tại một điểm bằng định nghĩa:

Bước 1: Tính $f\left(x\right)-f\left(x_0\right)$.

Bước 2: Lập và rút gọn tỉ số $\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$ với $x\in \left(a;b\right),x\ne x_0$.

Bước 3: Tìm giới hạn $\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$.

2. Đạo hàm của hàm số trên một khoảng

Hàm số y = f(x) được gọi là đạo hàm trên khoảng (a; b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x).

3. Ý nghĩa hình học của đạo hàm

- Hệ số góc tiếp tuyến của đồ thị hàm số y = f(x) tại điểm $M\left(x_0;f\left(x_0\right)\right)$ là $k=f^{\prime }\left(x_0\right)$ nếu đạo hàm $f^{\prime }\left(x_0\right)$ tồn tại.

- Phương tình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm $M\left(x_0;y_0\right)$, $y_0=f\left(x_0\right)$ là:

$y-y_0=f^{\prime }\left(x_0\right)\left(x-x_0\right)$.

4. Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời của chuyển động s = s(t) tại thời điểm t là v(t) = s’(t).

Sơ đồ tư duy Định nghĩa và ý nghĩa của đạo hàm

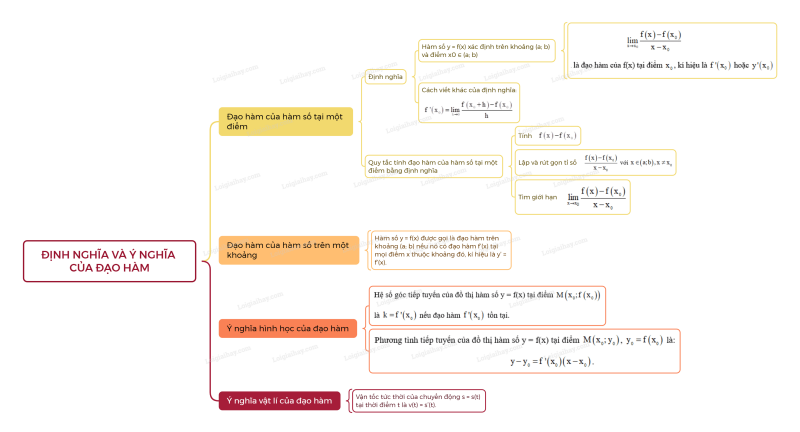
B. Bài tập Định nghĩa và ý nghĩa của đạo hàm

Đang cập nhật ...