Bài 19 trang 97 Toán 10 Tập 2: Tỉ lệ hộ nghèo (%) của 10 tỉnh/thành phố thuộc đồng bằng sông Hồng trong năm 2010 và năm 2016 được cho trong bảng sau:
|
Tỉnh/ thành phố |
Năm 2010 |
Năm 2016 |
|
Hà Nội |
5,3 |
1,3 |
|
Vĩnh Phúc |
10,4 |
2,9 |
|
Bắc Ninh |
7,0 |
1,6 |
|
Hải Dương |
10,8 |
2,3 |
|
Hải Phòng |
6,5 |
2,1 |
|
Hưng Yên |
11,1 |
2,6 |
|
Thái Bình |
10,7 |
3,7 |
|
Hà Nam |
12,0 |
4,4 |
|
Nam Định |
10,0 |
3,0 |
|
Ninh Bình |
12,2 |
4,3 |
(Theo Tổng cục Thống kê)
a) Tính số trung bình và độ lệch chuẩn của tỉ lệ hộ nghèo các tỉnh/thành phố thuộc đồng bằng sông Hồng trong các năm 2010, 2016.
b) Dựa trên kết quả nhận được, em có nhận xét gì về số trung bình và độ phân tán của tỉ lệ hộ nghèo các tỉnh/thành phố thuộc đồng bằng sông Hồng trong các năm 2010 và 2016.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Bài 18 trang 97 Toán 10 Tập 2: Các nhà toán học cổ đại Trung Quốc đã dùng phân số để xấp xỉ cho π.
a) Cho biết đâu là số đúng, đâu là số gần đúng.
b) Đánh giá sai số tuyệt đối, sai số tương đối của giá trị gần đúng này, biết
3,1415 < π < 3,1416.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Giải Toán 10 trang 97 Tập 2
Bài 17 trang 97 Toán 10 Tập 2: Trong đêm, một âm thanh cầu cứu phát ra từ một vị trí trong rừng và đã được hai trạm ghi tín hiệu ở các vị trí A, B nhận được. Khoảng cách giữa hai trạm là 16 km và trạm ở vị trí A nhận được tín hiệu sớm hơn 6 giây so với trạm ở vị trí B. Giả sử vận tốc âm thanh là 1 236 km/h. Hãy xác định phạm vi tìm kiếm vị trí phát ra âm thanh đó.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Bài 15 trang 96 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC có ba đỉnh A(– 1; 3), B(1; 2), C(4; – 2).
a) Viết phương trình đường thẳng BC.
b) Tính diện tích tam giác ABC.
c) Viết phương trình đường tròn có tâm A và tiếp xúc với đường thẳng BC.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Bài 9 trang 96 Toán 10 Tập 2: Cho hàm số y = f(x) = ax2 + bx + c với đồ thị là parabol (P) có đỉnh và đi qua điểm A(1; 2).
a) Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x – h)2 + k, trong đó I(h; k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).
c) Giải bất phương trình f(x) ≥ 0.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
B – Tự luận
Bài 7 trang 95 Toán 10 Tập 2: Cho các mệnh đề:
P: “Tam giác ABC là tam giác vuông tại A”;
Q: “Tam giác ABC có các cạnh thỏa mãn AB2 + AC2 = BC2”.
a) Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, ⇒ . Xét tính đúng sai của các mệnh đề này.
b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.
c) Gọi X là tập hợp các tam giác ABC vuông tại A, Y là tập hợp các tam giác ABC có trung tuyến AM = BC. Nêu mối quan hệ giữa hai tập hợp X và Y.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Bài 4 trang 95 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x + 2y – 5 = 0. Tìm mệnh đề sai trong các mệnh đề sau:
A. Vectơ là một vectơ pháp tuyến của Δ.
B. Vectơ là một vectơ chỉ phương của Δ.
C. Đường thẳng Δ song song với đường thẳng d: .
D. Đường thẳng Δ có hệ số góc k = 2.
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Giải bài tập Toán 10 Bài tập cuối năm
A – Trắc nghiệm
Giải Toán 10 trang 95 Tập 2
Bài 1 trang 95 Toán 10 Tập 2: Cho hệ bất phương trình bậc nhất hai ẩn . Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
A. (1; 1).
B. (2; 0).
C. (3; 2).
D. (3; – 2).
Giải Toán 10 (Kết nối tri thức): Bài tập cuối năm
Hoạt động 2 trang 94 Toán 10 Tập 2:
Đánh giá sai số của ước tính
Trong tiết thực hành trải nghiệm của lớp 10A, tổ của Hà đã thực hiện các bước trên, trong đó lặp lại bước 3 thêm hai lần: lần hai lấy 1 cốc lạc, lần ba lấy 1,5 cốc lạc và thu được kết quả như sau:
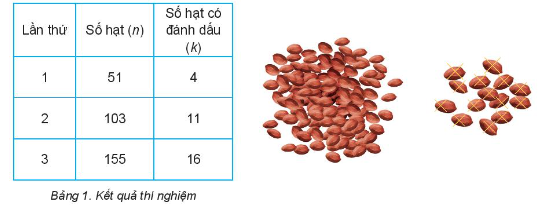
Giả sử số hạt lạc trong túi đựng là 1 000 (N = 1 000) và số hạt lạc được đánh dấu là 100 (M = 100). Kí hiệu là số quy tròn đến hàng đơn vị của đại lượng .
Dựa vào bảng số liệu trong Bảng 1, em hãy hoàn thành bảng tính theo mẫu sau:
|
Lần |
N |
M |
n |
k |
|
Sai số tuyệt đối |
Sai số tương đối |
|
1 |
1 000 |
100 |
51 |
4 |
? |
? |
? |
|
2 |
1 000 |
100 |
? |
? |
? |
? |
? |
|
3 |
1 000 |
100 |
? |
? |
? |
? |
? |
Bảng 2. Tính sai số
Em có nhận xét gì về sai số của việc tính xấp xỉ số hạt lạc trong túi khi n càng lớn?
Giải Toán 10 (Kết nối tri thức): Ước tính số cá thể trong một quần thể
Hoạt động 1 trang 93 Toán 10 Tập 2:
Ước tính số hạt lạc trong một hộp
Chuẩn bị:
- Cốc;
- Giấy, bút;
- Một túi lạc.
Tiến hành
Bước 1. Lấy ra một cốc lạc từ trong túi, đếm số lượng và đánh dấu từng hạt lạc.
Bước 2. Đổ lạc đã được đánh dấu vào lại trong túi và xáo trộn đều.
Bước 3. Lấy ra nửa cốc lạc, đếm tổng số hạt lạc và số hạt lạc có đánh dấu trong cốc.
Gọi N là tổng số hạt lạc trong túi ban đầu. Hãy dùng kết quả đếm được ở bước 3 để ước tính N.
Giải Toán 10 (Kết nối tri thức): Ước tính số cá thể trong một quần thể
4. Thực hành trải nghiệm trong phòng máy
Thực hiện vẽ hình với phần mềm GeoGebra.
- Vẽ đường tròn (A; R) và điểm B nằm ngoài đường tròn đó. Lấy một điểm C trên đường tròn (A; R) và vẽ M là giao điểm của AC và đường trung trực của đoạn thẳng BC. Cho điểm C thay đổi và dùng lệnh tìm quỹ tích để thấy rằng M thay đổi trên một nhánh hypebol.
Các bước thực hiện như sau:
Bước 1: Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2: Vẽ đường tròn (A; R):
Chẳng hạn, lấy R = 5, ta vẽ đường tròn (A; 5) như sau: Trên thanh công cụ chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào một điểm bất kì trên vùng làm việc để có tâm A → Nhập số 5 ứng với bán kính của đường tròn như hình vẽ dưới đây:
→ Nhấn chuột trái vào một điểm bất kì trên vùng làm việc để có tâm A → Nhập số 5 ứng với bán kính của đường tròn như hình vẽ dưới đây:

Nhấn “OK”, ta được đường tròn như hình vẽ:
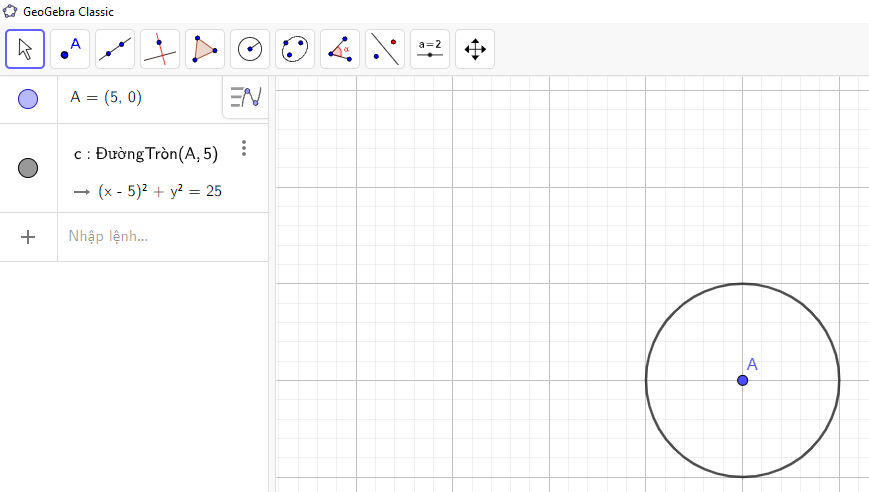
Bước 3: Lấy 1 điểm B bất kì nằm ngoài đường tròn.
Trên thanh công cụ ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào một điểm nằm ngoài đường tròn như hình vẽ:
→ Nhấn chuột trái vào một điểm nằm ngoài đường tròn như hình vẽ:
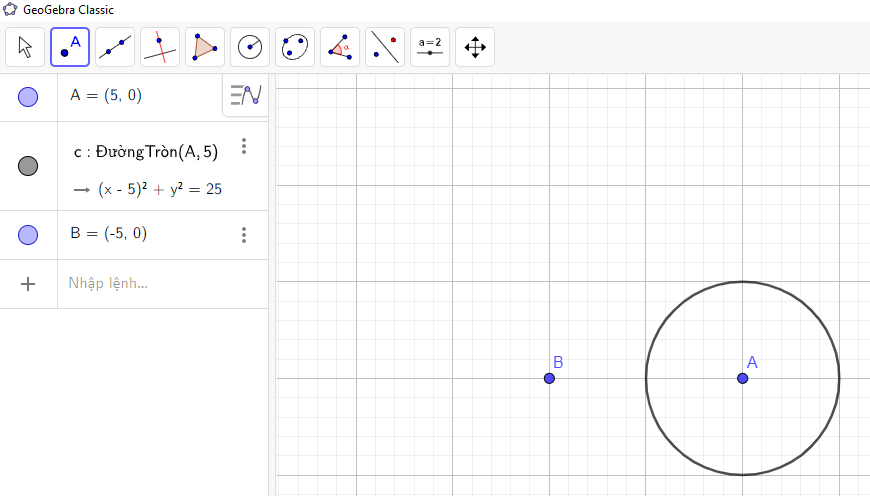
Bước 4: Lấy một điểm C trên đường tròn:
Ta nhấn chuột trái vào một điểm trên đường tròn đã vẽ, ta được điểm C như hình vẽ:
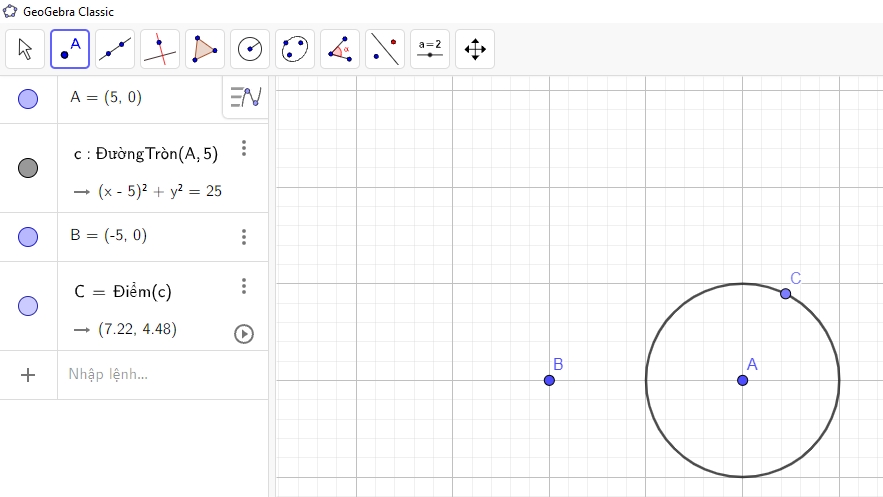
Bước 5: Vẽ đường thẳng AC
Trên thanh công cụ, ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào hai điểm A và C ta được hình vẽ:
→ Nhấn chuột trái vào hai điểm A và C ta được hình vẽ:
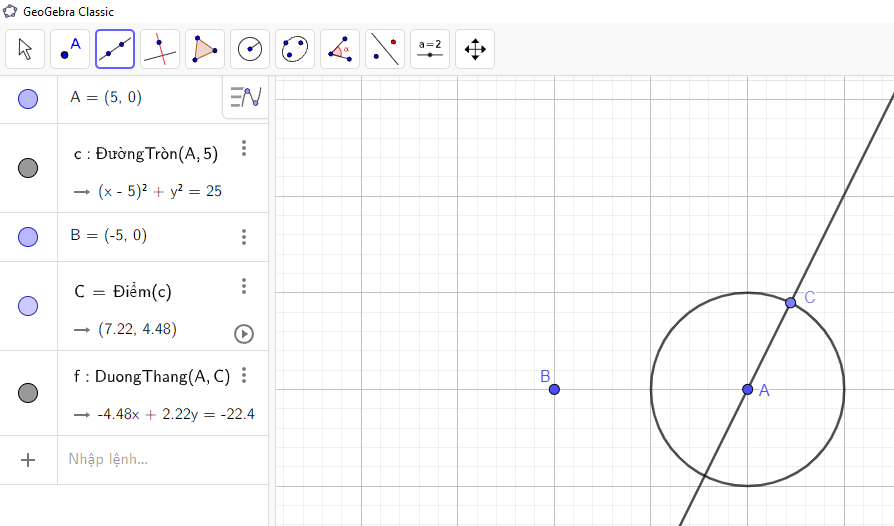
Bước 6: Vẽ đoạn thẳng BC:
Trên thanh công cụ, ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào điểm B và điểm C ta được hình vẽ:
→ Nhấn chuột trái vào điểm B và điểm C ta được hình vẽ:
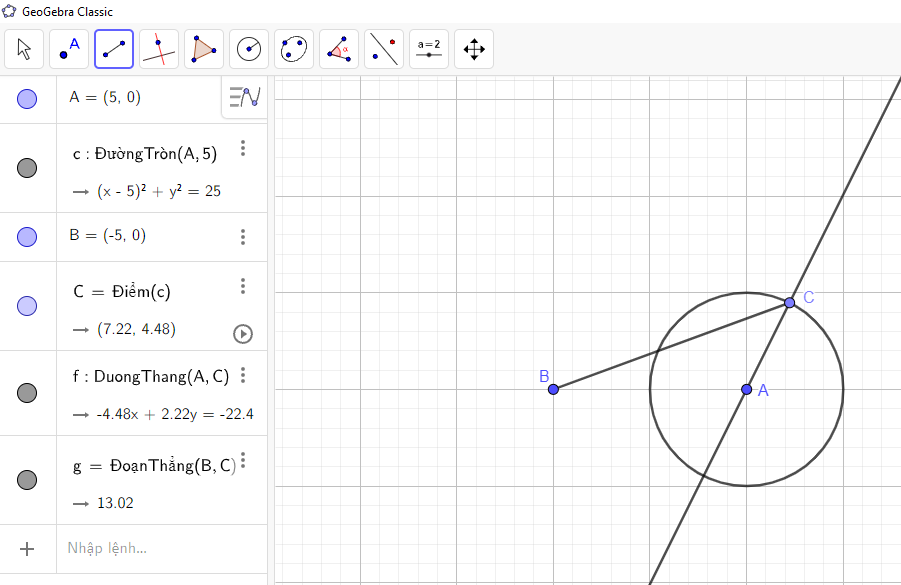
Bước 7: Vẽ đường trung trực của đoạn thẳng BC:
Trên thanh công cụ, chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào hai điểm B và C ta được như hình vẽ:
→ Nhấn chuột trái vào hai điểm B và C ta được như hình vẽ:
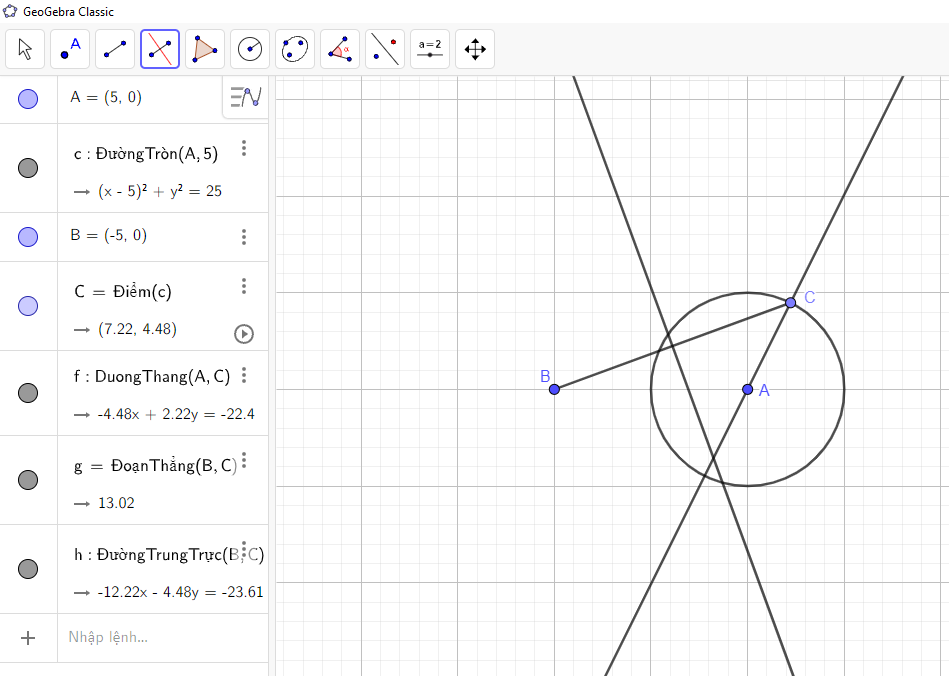
Bước 8: Lấy giao điểm của AC và trung trực của đoạn thẳng BC:
Trên thanh công cụ, ta chọn ![]() → Chọn
→ Chọn ![]() → Nhấn chuột trái vào đường thẳng AC và trung trực đoạn thẳng BC ta được như hình vẽ:
→ Nhấn chuột trái vào đường thẳng AC và trung trực đoạn thẳng BC ta được như hình vẽ:
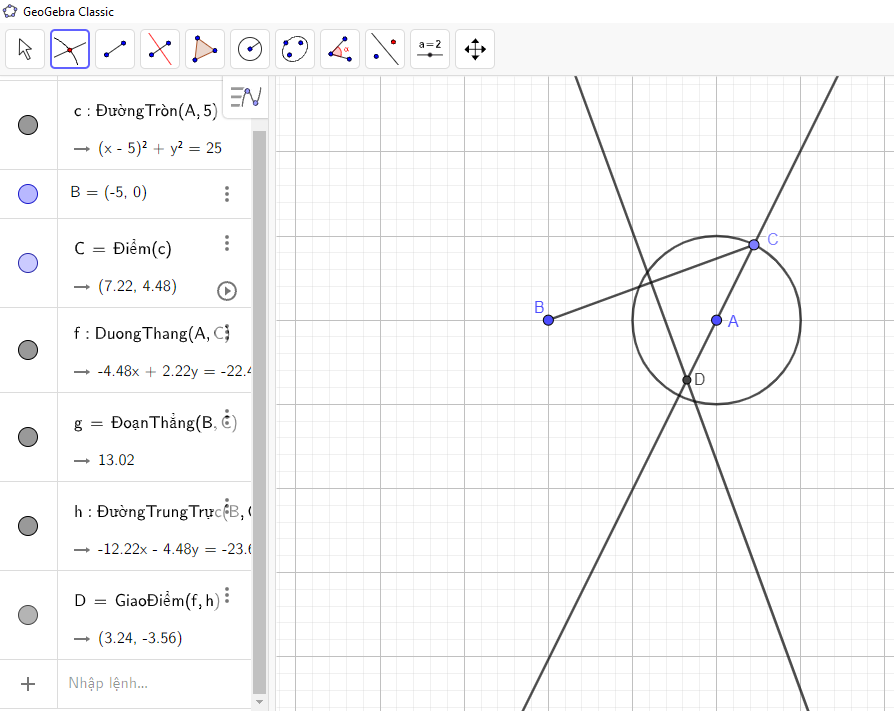
Bước 9: Đổi tên giao điểm D thành giao điểm M:
Trên thanh công cụ, chọn ![]() → Nhấn chuột trái vào điểm D → Nhấn chuột phải → Chọn
→ Nhấn chuột trái vào điểm D → Nhấn chuột phải → Chọn ![]() để đổi D thành M.
để đổi D thành M.

Nhấn “OK”, ta được như hình vẽ:
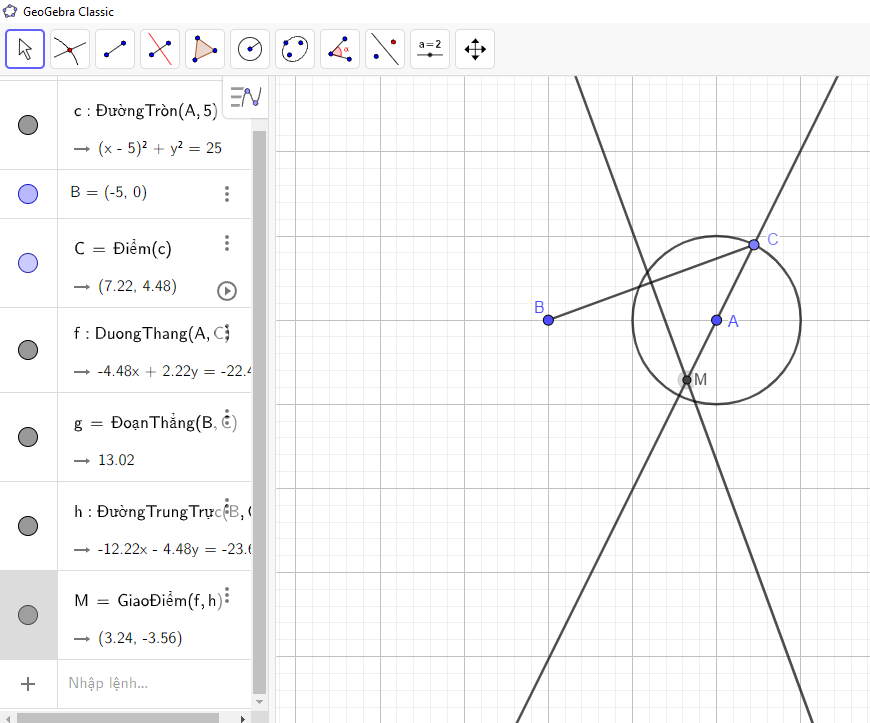
Bước 10: Cho điểm M hiện thị dấu vết khi di chuyển:
Nhấn chuột trái chọn điểm M → Nhấn chuột phải → Chọn ![]()
Bước 11: Cho điểm C di chuyển trên đường tròn (A; R):
Nhấn chuột trái chọn điểm C → Nhấn chuột phải → Chọn ![]()
Khi đó điểm C di chuyển dẫn đến M di chuyển trên một hypebol như hình vẽ
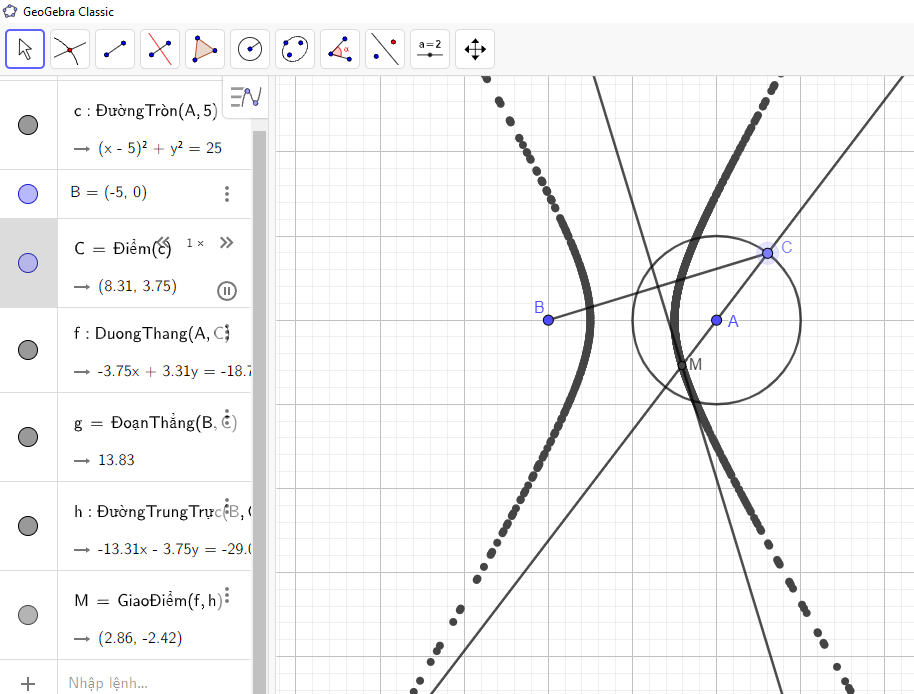
- Tương tự ta thực hiện các hình vẽ sau:
- Vẽ đường tròn (A; R) và điểm B nằm trong đường tròn đó. Lấy một điểm C trên đường tròn (A; R) và vẽ M là giao điểm của AC và đường tròn trung trực của đoạn thẳng BC. Cho điểm C thay đổi và dùng lệnh tìm quỹ tích để thấy M thay đổi trên một elip.
Vẽ tương tự như hoạt động trên, chỉ khác tại Bước 3, điểm B thay vì nằm ngoài đường tròn thì ta lấy bên trong đường tròn.
Khi đó, điểm C di chuyển thì ta được M chạy trên một elip như hình vẽ:
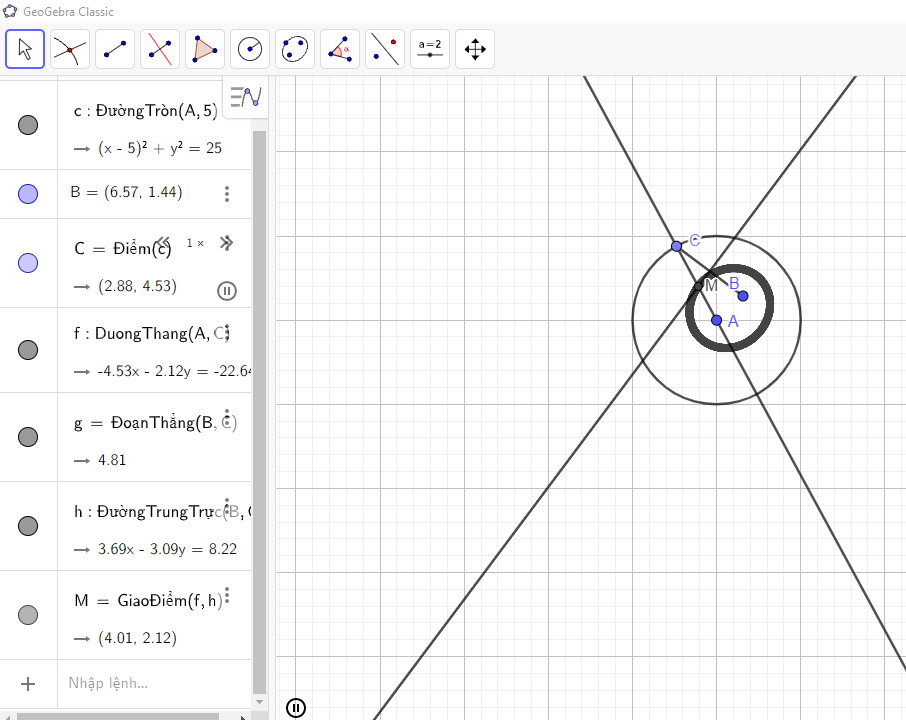
- Vẽ một số đường tròn (ω1), (ω2), (ω3), … có cùng tâm O1 tương ứng có bánh kính R1, R1 + a, R1 + 2a, … và một số đường tròn (Ω1), (Ω2), (Ω3), … có cùng tâm O2, tương ứng có bán kính R2, R2 + a, R2 + 2a, … (R1 ≠ R2). Khi đó, em sẽ quan sát thấy các cặp giao điểm A1, B1; A2, B2; A3, B3; … tương ứng của (ω1) và (Ω1); (ω2) và (Ω2); (ω3) và (Ω3); … là cùng thuộc một nhánh của một hypebol. Kết quả này tương ứng với một hiện tượng vật lí mà em có thể quan sát được: Ném hai hòn sỏi (bằng nhau) xuống mặt hồ lặng sóng, thì em sẽ thấy hai họ đường tròn sóng nước và nói chung giao của chúng tạo nên một đường hypebol.
Chẳng hạn, ta lấy R1 = 3, R2 = 5 và a = 1, ta vẽ được các đường tròn trên như sau:
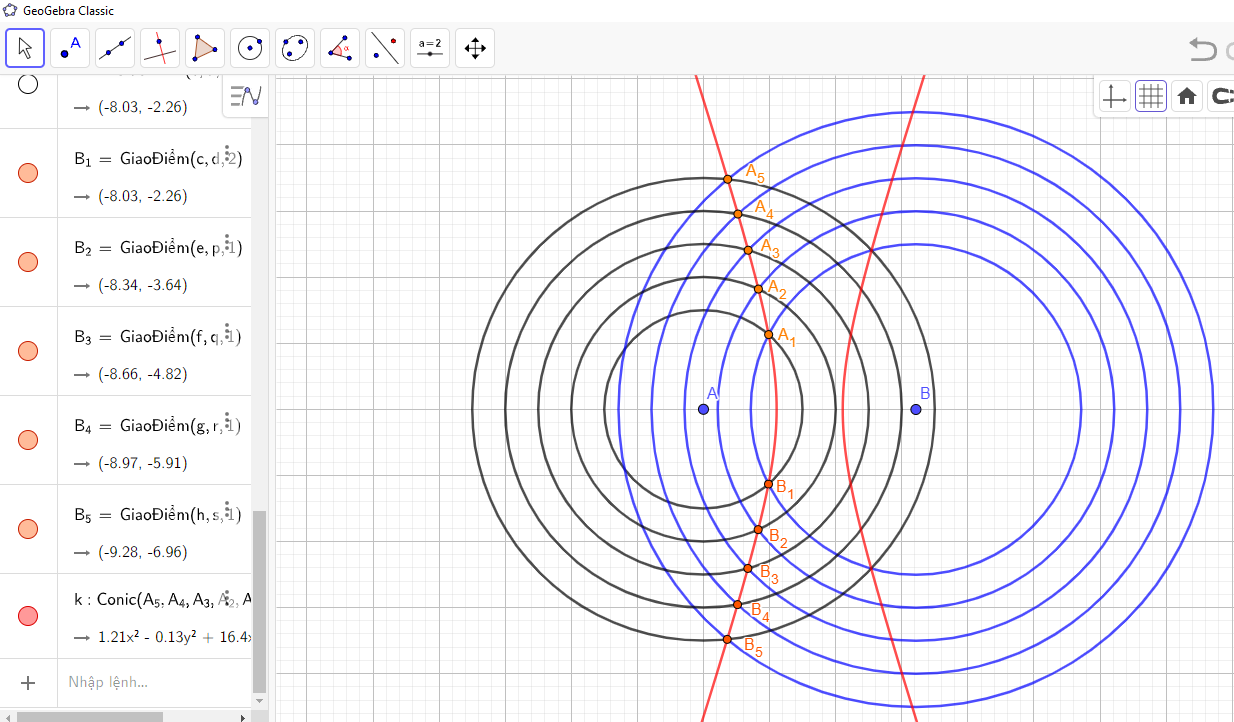
Bài làm:
Giải Toán 10 (Kết nối tri thức): Một số nội dung cho hoạt động trải nghiệm hình học
3. Gấp giấy, đo đạc và xác định các yếu tố của ba đường conic
Cách xác định các yếu tố của:
a) Một hình elip đã được vẽ trên giấy.
Bước 1: Ta xác định được hai trục đối xứng của elip bằng cách gấp giấy.
Giả sử một trục đối xứng cắt elip tại A1, A2 và trục đối xứng còn lại cắt elip tại B1, B2 (với A1A2 ≥ B1B2).
Bước 2: Chọn hệ trục tọa độ Oxy, có O là giao của hai trục đối xứng, tia Ox trùng với tia OA2, tia Oy trùng với tia OB2, chọn đơn vị đo trên mặt phẳng tọa độ là cm.
Bước 3: Trong mặt phẳng tọa độ Oxy, elip có phương trình chính tắc là
Đo độ dài các đoạn A1A2, B1B2 (đơn vị: cm), ta tính được a, b.
Bước 4: Xác định tiêu cự và vị trí các tiêu điểm.
b) Một hypebol đã được vẽ trên giấy.
Bước 1: Ta xác định được hai trục đối xứng của hypebol bằng cách gấp giấy.
Giả sử một trục đối xứng cắt hypebol tại A1, A2.
Bước 2: Chọn hệ trục tọa độ Oxy, có O là giao của hai trục đối xứng, tia Ox trùng với tia OA2, tia Oy trùng với trục đối xứng còn lại.
Bước 3: Trong mặt phẳng tọa độ Oxy, hypebol có phương trình chính tắc là
Lấy hai điểm trên hypebol, đo trực tiếp (đơn vị: cm) để xác định tọa độ của hai điểm đó, rồi thay vào phương trình trên từ đó tính được a, b.
Bước 4: Xác định tiêu cự và vị trí các tiêu điểm.
c) Một parabol đã được vẽ trên giấy
Bước 1: Ta xác định được hai trục đối xứng và đỉnh của parabol bằng cách gấp giấy.
Bước 2: Chọn hệ trục toạ độ Oxy, có O là giao của hai trục đối xứng cũng đồng thời là đỉnh của parabol, thoả mãn parabol có phương trình chính tắc y2 = 2px (đơn vị: cm).
Bước 3: Lấy một điểm trên parabol, đo trực tiếp (đơn vị: cm) để xác định tọa độ của điểm đó, rồi thay vào phương trình parabol để tính p.
Bước 4: Xác định tâm sai, vị trí tiêu điểm và đường chuẩn.
Bài làm:
Giải Toán 10 (Kết nối tri thức): Một số nội dung cho hoạt động trải nghiệm hình học
2. Sử dụng kết quả hình học để tính toán trong đo đạc thực tế
Chia nhóm lớp (tùy thuộc vào sĩ số mỗi lớp) và chọn các đối tượng đo đạc khác nhau tương ứng với hai bài toán:
Bài toán 1: Xác định khoảng cách từ vị trí đứng tới một vị trí khác (theo các bước tương ứng được đề cập trong Ví dụ 4, trang 40 của Bài 6, Tập một, SGK).
Bài toán 2: Xác định khoảng cách giữa hai vị trí A, B khác vị trí đứng C.
Đối với bài toán 2, ta cần thực hiện các bước như ở bài toán 1, để xác định khoảng cách từ C tới A và khoảng cách từ C tới B, sau đó, xác định góc C của tam giác ABC.
Khi đó ta tính AB dựa vào định lí côsin đã được học.
Bài làm:
Giải Toán 10 (Kết nối tri thức): Một số nội dung cho hoạt động trải nghiệm hình học
Giải bài tập Toán 10 Một số nội dung cho hoạt động trải nghiệm hình học
1. Kiểm tra tính đúng đắn của một kết quả hình học thông qua những ví dụ cụ thể
Chia nhóm lớp (tùy thuộc vào sĩ số mỗi lớp) và chọn một kết quả hình học để kiểm tra, chẳng hạn:
a) Định lí sin đối với một tam giác nội tiếp trong một đường tròn:
Cho tam giác ABC nội tiếp đường tròn. Sử dụng thước đo độ dài để đo độ dài các cạnh và độ dài bán kính của tam giác, thước đo góc để đo các góc của tam giác và máy tính bỏ túi (lấy kết quả gần đúng) để kiểm tra định lí sin:
b) Định lí côsin đối với một tam giác:
Cho tam giác ABC. Sử dụng thước đo độ dài để đo độ dài các cạnh của tam giác, thước đo góc để đo các góc của tam giác và máy tính bỏ túi (lấy kết quả gần đúng) để kiểm tra định lí côsin:
BC2 = AB2 + AC2 – 2AB.AC.cosA;
AC2 = AB2 + BC2 – 2AB.BC.cosB;
AB2 = AC2 + BC2 – 2AC.BC.cosC.
c) Đẳng thức đối với tam giác:
Cho tam giác ABC. Sử dụng thước đo độ dài để đo độ dài các cạnh, độ dài chiều cao ha (kẻ từ A) của tam giác và máy tính bỏ túi để kiểm tra đẳng thức:
Bài làm:
Giải Toán 10 (Kết nối tri thức): Một số nội dung cho hoạt động trải nghiệm hình học
Giải Toán 10 trang 89 Tập 2
Bài tập 9.20 trang 89 Toán 10 Tập 2: Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất của các biến cố:
F: “Trong ba ngày, có đúng một ngày có mưa”;
G: “Trong ba ngày, có ít nhất hai ngày không mưa”.
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 9
B. Tự luận
Bài tập 9.17 trang 88 Toán 10 Tập 2: Một hộp đựng bảy thẻ màu xanh đánh số từ 1 đến 7; năm thẻ màu đỏ đánh số từ 1 đến 5 và hai thẻ màu vàng đánh số từ 1 đến 2 . Rút ngẫu nhiên ra một tấm thẻ.
a) Mô tả không gian mẫu.
b) Mỗi biến cố sau là tập con nào của không gian mẫu?
A: “Rút ra được thẻ màu đỏ hoặc màu vàng”;
B: “Rút ra được thẻ mang số hoặc là 2 hoặc là 3”.
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 9
Bài tập 9.16 trang 88 Toán 10 Tập 2: Một tổ trong lớp 10T có 4 bạn nữ và 3 bạn nam. Giáo viên chọn ngẫu nhiên hai bạn trong tổ đó tham gia đội làm báo của lớp. Xác suất để hai bạn được chọn có một bạn nam và một bạn nữ là
A. .
B. .
C. .
D. .
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 9
Giải bài tập Toán 10 Bài tập cuối chương 9
A. Trắc nghiệm
Giải Toán 10 trang 88 Tập 2
Bài tập 9.13 trang 88 Toán 10 Tập 2: Một hộp có bốn loại bi: bi xanh, bi đỏ, bi trắng và bi vàng. Lấy ngẫu nhiên ra một viên bi. Gọi E là biến cố: “Lấy được viên bi đỏ”. Biến cố đối của E là biến cố
A. Lấy được viên bi xanh.
B. Lấy được viên bi vàng hoặc bi trắng.
C. Lấy được viên bi trắng.
D. Lấy được viên bi vàng hoặc bi trắng hoặc bi xanh.
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 9
Bài tập 9.12 trang 87 Toán 10 Tập 2: Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gen là gen trội A và gen lặn a. Hình dạng hạt của đậu Hà Lan có hai kiểu hình là hạt trơn và hạt nhăn tương ứng với hai loại gen là gen trội B và gen lặn b. Biết rằng, cây con lấy ngẫu nhiên một gen từ cây bố và một gen từ cây mẹ.
Phép thử là cho lai hai loại đậu Hà Lan, trong đó cả cây bố và cây mẹ đều có kiểu gen là (Aa,Bb) và kiểu hình là hạt màu vàng và trơn. Giả sử các kết quả có thể là đồng khả năng. Tính xác suất để cây con cũng có kiểu hình là hạt màu vàng và trơn.
Giải Toán 10 (Kết nối tri thức) Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển
Giải Toán 10 trang 87 Tập 2
Bài tập 9.10 trang 87 Toán 10 Tập 2: Trên một phố có hai quán ăn X, Y. Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của biến cố “Hai bạn vào quán X, bạn còn lại vào quán Y”.
Giải Toán 10 (Kết nối tri thức) Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển
