30 câu Trắc nghiệm Hình bình hành (có đáp án 2024) – Toán 8 Cánh diều

Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 4: Hình bình hành đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 4.

1 119 lượt xem

Bài trước

Bài sau

Trắc nghiệm Toán 8 Bài 4: Hình bình hành

Câu 1 : Cho hình bình hành ABCD có $\hat{A} = 120^{o}$ , các góc còn lại của hình bình hành là:

A
$\hat{B} = 60^{o}; \hat{C} = 120^{o}; \hat{D} = 60^{o}$
B
$\hat{B} = 110^{o}; \hat{C} = 80^{o}; \hat{D} = 60^{o}$
C
$\hat{B} = 80^{o}; \hat{C} = 120^{o}; \hat{D} = 80^{o}$
D
$\hat{B} = 120^{o}; \hat{C} = 60^{o}; \hat{D} = 120^{o}$

Đáp án : A

Lời giải :

Trong hình bình hành các góc đối bằng nhau:

\hat{A} = \hat{C}; \hat{B} = \hat{D}

và

\hat{A} + \hat{B} = 180^{o}

Nên $\hat{A} = \hat{C} = 120^{o}; \hat{B} = \hat{D} = 60^{o}$

Hình bình hành có các góc đối bằng nhau

Câu 2 : Cho hình bình hành ABCD. Qua giao điểm O của các đường chéo, vẽ một đường thẳng cắt các cạnh đối BC và AD theo thứ tự E và F (đường thẳng này không đi qua trung điểm của BC và AD). Chọn các khẳng định đúng:

A
AF = CE
B
AF = BE
C
DF = CE
D
DF = DE.

Đáp án : A

Lời giải :

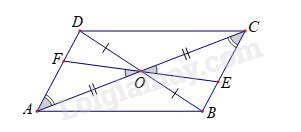
$Δ A O F = Δ C O E$ (g – c – g) suy ra AF = CE

Câu 3 : Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.

A
bằng nhau.
B
cắt nhau.
C
cắt nhau tại trung điểm mỗi đường.
D
song song.

Đáp án : C

Lời giải :

Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.

Câu 4 : Cho hình bình hành ABCD. Gọi H, K lần lượt là hình chiếu của A, C trên đường thẳng BD. Chọn khẳng định đúng:

A
AH = HC.
B
AH // BC
C
AH = AK.
D
AHCK là hình bình hành.

Đáp án : D

Lời giải :

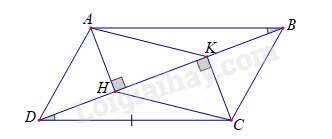
Xét tam giác AHB và CKD có: $\hat{A H B} = \hat{C K D} = 90^{o}$ ; AB = CD; $\hat{A B H} = \hat{C D K}$

$\Rightarrow Δ A H B = Δ C K D \Rightarrow A H = C K (1)$

Lại có: $A H ⊥ B D; C K ⊥ B D \Rightarrow A H / / C K (2)$

Từ (1), (2) suy ra AHCK là hình bình hành.

Câu 5 : Chu vi của hình bình hành ABCD bằng 10 cm, chu vi của tam giác ABD bằng

9 cm. Khi đó độ dài BD là:

A
4 cm
B
6 cm
C
2 cm
D
1 cm

Đáp án : A

Lời giải :

Vì chu vi của hình bình hành ABCD bằng 10 cm nên:

AB + BC + CD + DA = 10

$\Rightarrow A B + D A = 5$

Chu vi của tam giác ABD bằng 9 cm nên: $A B + B D + D A = 9 \Rightarrow B D = 4 c m$

Câu 6 : Hãy chọn câu trả lời đúng

A
Tứ giác có hai cạnh đối song song là hình bình hành.
B
Tứ giác có hai cạnh đối bằng nhau là hình bình hành.
C
Tứ giác có hai góc đối bằng nhau là hình bình hành.
D
Tứ giác có các cạnh đối song song là hình bình hành.

Đáp án : D

Lời giải :

Dấu hiệu nhận biết: Tứ giác có các cạnh đối song song là hình bình hành.

Câu 7: Hãy chọn câu trả lời “sai”

A
Tứ giác có hai cặp cạnh đối song song là hình bình hành.
B
Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.
C
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
D
Tứ giác có hai cặp góc đối bằng nhau là hình bình hành.

Đáp án : B

Lời giải :

Dấu hiệu nhận biết:

+ Tứ giác có các cạnh đối song song là hình bình hành nên A đúng.

+ Tứ giác có các cạnh đối bằng nhau là hình bình hành nên C đúng.

+ Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng.

Câu 8 : Hãy chọn câu trả lời “sai”

A
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
B
Hình thang có hai cạnh bên song song là hình bình hành.
C
Hình thang có hai đường chéo bằng nhau là hình bình hành.
D
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Đáp án : C

Lời giải :

Dấu hiệu nhận biết:

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên A, B đúng.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên D đúng.

Câu 9 : Hình bình hành ABCD thỏa mãn:

A
Tất cả các góc đều nhọn
B
$\hat{A} + \hat{B} = 180^{o}$
C
Góc B và góc C đều nhọn
D
Góc A vuông còn góc B nhọn

Đáp án : B

Lời giải :

Trong hình bình hành các cạnh đối song song các góc đối bằng nhau:

\hat{A} = \hat{C};^{} \hat{B} = \hat{D}

và

\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360^{o}

nên hai góc kề nhau có tổng bằng

180^{o}

Câu 10 : Hãy chọn câu trả lời đúng

A
Trong hình bình hành hai đường chéo bằng nhau.
B
Trong hình bình hành hai góc kề một cạnh phụ nhau.
C
Đường thẳng đi qua giao điểm của hai đường chéo là trục đối xứng của hình bình hành đó.
D
Trong hình bình hành hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Đáp án : D

Lời giải :

Trong hình bình hành hai đường chéo cắt nhau tại trung điểm của mỗi đường.

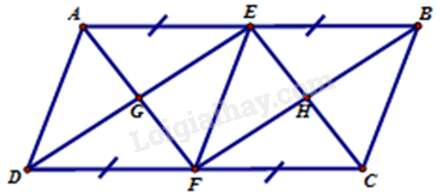
Câu 11 : Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:

A
6 hình bình hành
B
5 hình bình hành
C
4 hình bình hành
D
3 hình bình hành

Đáp án : A

Lời giải:

+ Vì ABCD là hình bình hành nên AB // CD, AD // BC

+ Xét tam giác AEFD có AE = FD; AE // FD (do AB // CD) nên AEFD là hình bình hành.

+ Xét tứ giác BEFC có BE = FC; BE // FC (do AB // CD) nên BEFC là hình bình hành

+ Xét tứ giác AECF có AE = FC; AE // FC (do AB // CD) nên AEFC là hình bình hành

+ Xét tứ giác BEDF có BE = FD, BE //FD (do AB // CD) nên BEDF là hình bình hành

+ Vì AECF là hình bình hành nên AF // EC ⇒ EH // GF; vì BEDF là hình bình hành nên ED // BF ⇒ EG // HF

Suy ra EGHF là hình bình hành

Vậy có tất cả 6 hình bình hành: ABCD; AEFD; BEFC; AECF; BEDF; EGHF

Câu 12 : Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:

A
DE = BF
B
DE > BF
C
DE < BF
D
DE = EB

Đáp án : A

Lời giải :

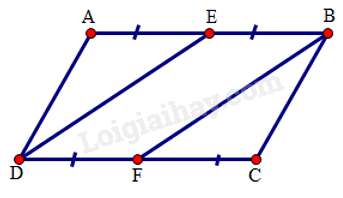
Vì ABCD là hình bình hành nên AB // CD; AB = CD

+ Xét tứ giác BEDF có BE =FD; BE // FD (do AB // CD) nên BFDE là hình bình hành.

Từ đó: DE = BF (tính chất hình bình hành)

Câu 13 : Hai góc kề nhau của một hình bình hành không thể có số đo là:

A
600; 1200
B
400; 500
C
1300; 500
D
750; 1050

Đáp án : B

Lời giải :

Trong hình bình hành có các góc đối nhau và tổng các góc trong hình bình hành phải bằng 3600 nên ta có:

600.2 + 1200.2 = 3600

400.2 + 500.2 = 1800 ≠ 3600

1300.2 + 500.2 = 3600

1050.2 + 750.2 = 3600

Do đó hai góc kề của hình bình hành không thể có số đo 400; 500

Câu 14 : Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?

A
Hình thang
B
Hình bình hành
C
Hình thang cân
D
Hình thang vuông

Đáp án : B

Lời giải :

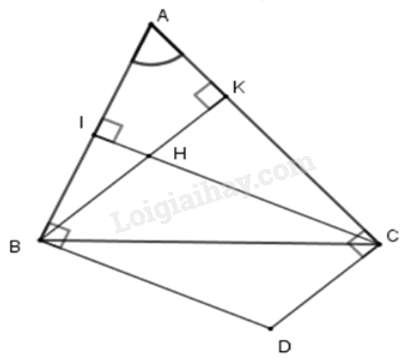
Gọi BK, CI là các đường cao của tam giác ABC. Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).

Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB) và CD // BH (cùng vuông với AC)

Suy ra tứ giác BHCD là hình bình hành

Câu 15 : Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu sai.

A
BH // CD
B
CH // BD
C
BH = CD
D
HB = HC

Đáp án : D

Lời giải:

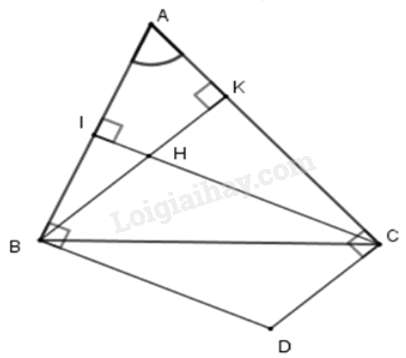
Gọi BK, CI là các đường cao của tam giác ABC. Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).

Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB) và CD // BH (cùng vuông với AC)

Suy ra tứ giác BHCD là hình bình hành (dhnb)

Từ đó HB = CD; CH = BD nên D sai (ta chưa đủ điều kiện để chỉ ra được HB = HC)

Câu 16 : Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là các điểm sao cho MN // AC; $M N = \frac{1}{2} A C$ ; PQ // AC; $P Q = \frac{1}{2} A C$ . Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.

A
Hình bình hành
B
Hình thang vuông
C
Hình thang cân
D
Hình thang

Đáp án : A

Lời giải :

Nối AC.

Xét tam giác EAC suy ra MN // AC; $M N = \frac{1}{2} A C$ (1)

Xét tam giác FAC suy ra PQ // AC; $P Q = \frac{1}{2} A C$ (2)

Từ (1) và (2) suy ra PQ // NM; PQ = MN nên MNPQ là hình bình hành.

Câu 17 : Tỉ số độ dài hai cạnh của hình bình hành là 3 : 5. Còn chu vi của nó bằng 48cm. Độ dài cạnh kề của hình bình hành là:

A
12cm và 20cm
B
6cm và 10cm
C
3cm và 5cm
D
9cm và 15cm

Đáp án : D

Lời giải :

Gọi độ dài hai cạnh của hình bình hành là a và b với a, b > 0

Theo bài ra ta có: $\frac{a}{3} = \frac{b}{5}$

Nửa chu của hình bình hành là: 48 : 2 = 24cm

Suy ra: a + b = 24cm. Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{a}{3} = \frac{b}{5} = \frac{a + b}{3 + 5} = \frac{24}{8} = 3$

⇒ a = 3.3 = 9; b = 3.5 = 15

Vậy hai cạnh của hình bình hành là 9cm và 15cm

Câu 18 : Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho $B E = D F < \frac{1}{2} B D$ . Chọn khẳng định đúng.

A
FA = CE
B
FA < CE
C
FA > CE
D
Chưa kết luận được

Đáp án : A

Lời giải:

Gọi O là giao điểm của AC và BD. Ta có OA = OC, OB = OD

Mà BE = DF (gt) ⇒ OE = FO.

Tứ giác AECF có hai đường chéo AC và EF cắt nhau tại trung điểm O nên AECF là hình bình hành

⇒ FA = CE

Câu 19 : Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Tính số đo góc BDC, biết $\hat{B A C} = 50^{o}$ .

A
500
B
1000
C
1500
D
1300

Đáp án : D

Lời giải :

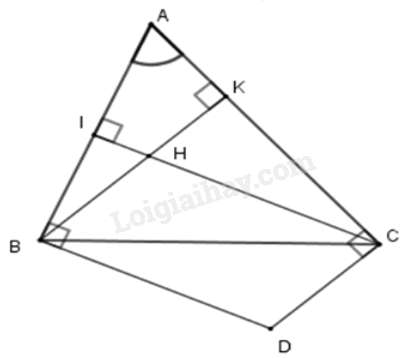
Xét tứ giác AIHK có:

$\hat{A} + \hat{A I H} + \hat{I H K} + \hat{A K H} = 360^{o}$ (định lí tổng các góc trong của tứ giác)

$\Rightarrow \hat{A H K} = 360^{o} - 50^{o} - 90^{o} - 90^{o} = 130^{o}$

Suy ra: $\hat{B H C} = \hat{I H K} = 130^{o}$ (hai góc đối đỉnh)

Vì tứ giác BHCD là hình bình hành nên: $\hat{B D C} = \hat{B H C} = 130^{o}$

Vậy $\hat{B D C} = 130^{o}$

Câu 20 : Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.

A
DE = FE; FE > FB
B
DE = FE = FB
C
DE > FE; EF = FB
D
DE > FE > FB

Đáp án : B

Lời giải :

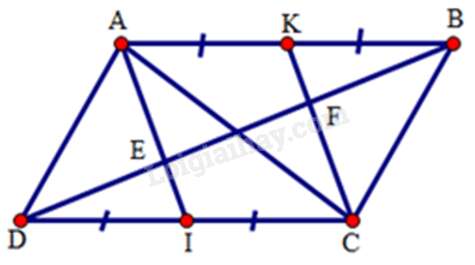
Vì $A K = \frac{A B}{2}; I C = \frac{C D}{2}$ (gt) mà AB = CD (cạnh đối hình bình hành) nên

AK = IC

Vì AB // CD (gt), K Є AB, I Є DC ⇒ AK // IC

Tứ giác AKCI có AK // IC, AK = IC (cmt) nên là hình bình hành. Suy ra AI // CK.

Mà E Є AI, F Є CK ⇒ EI // CF, KF // AE

Xét ΔDCF có: DI = IC (gt); IE // CF (cmt) ⇒ ED = FE (1)

Xét ΔABE có: AK = KB (gt), KF // AE (cmt) ⇒ EF = FB (2)

Từ (1) và (2) suy ra ED = FE = FB

Câu 21 : Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA sao cho ME // AB; $M E = \frac{A B}{2}$ . Tứ giác ADME là:

A
Hình thang
B
Hình bình hành
C
Hình thang cân
D
Hình thang vuông

Đáp án : B

Lời giải:

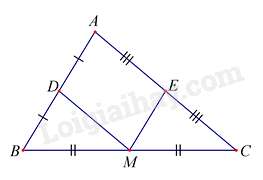
Vì $E A = E C (g t), M B = M C (g t)$

Vì $M E / / A B$ và $M E = \frac{A B}{2}$

Lại có: $A D = D B = \frac{A B}{2} \Rightarrow A D = M E$ nên ADME là hình bình hành.

Câu 22 : Hình bình hành ABCD có $\hat{A} - \hat{B} = 20^{o}$ . Số đo góc A bằng:

A
$80^{o}$
B
$90^{o}$
C
$100^{o}$
D
$110^{o}$

Đáp án : C

Lời giải :

Ta có ABCD là hình bình hành nên $\hat{A} + \hat{B} = 180^{o}$ mà $\hat{A} - \hat{B} = 20^{o} \Rightarrow \hat{A} = 100^{o}$

Câu 23 : Cho hình bình hành có $\hat{A} = 3 \hat{B}$ . Số đo các góc của hình bình hành là:

A
$\hat{A} = \hat{C} = 90^{o}; \hat{B} = \hat{D} = 30^{o}$
B
$\hat{A} = \hat{D} = 135^{o}; \hat{B} = \hat{C} = 45^{o}$
C
$\hat{A} = \hat{D} = 90^{o}; \hat{B} = \hat{C} = 30^{o}$
D
$\hat{A} = \hat{C} = 135^{o}; \hat{B} = \hat{D} = 45^{o}$

Đáp án : D

Lời giải :

Tứ giác ABCD là hình bình hành nên

\hat{A} + \hat{B} = 180^{o}

mà

\hat{A} = 3 \hat{B}

$\Rightarrow 4 \hat{B} = 180^{o} \Rightarrow \hat{B} = 45^{o}; \hat{A} = 135^{o}$

Trong hình bình hành ABCD có các góc đối bằng nhau nên $\hat{A} = \hat{C} = 135^{o}; \hat{B} = \hat{D} = 45^{o}$

Câu 24 : Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là thuộc các cạnh AF, EC, BF, DE và $F N = \frac{1}{2} D E; F N / / D E$ ; $E M = \frac{1}{2} B F; E M / / B F$ . Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.

A
Hình bình hành
B
Hình thang vuông
C
Hình thang cân
D
Hình thang

Đáp án : A

Lời giải :

Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.

Xét tam giác CED ta có: ${\begin{matrix} F N = \frac{1}{2} D E = E Q \\ F N / / E D \Rightarrow F N / / E Q \end{matrix}$

⇒ NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)

Xét tam giác ABF ta có: ${\begin{matrix} E M = \frac{1}{2} B F = P F \\ E M / / B F \Rightarrow E M / / P F \end{matrix}$

⇒ EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)

Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành

Câu 25 : Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AD, BC. Đường chéo AC cắt BE, DF theo thứ tự ở K, I. Chọn khẳng định đúng nhất.

A
K, I lần lượt là trọng tâm ΔABD, ΔCBD
B
AK = KI = IC
C
Cả A, B đều đúng
D
Cả A, B đều sai

Đáp án : C

Lời giải:

Gọi O là giao điểm của AC, BD

Vì ABCD là hình bình hành nên AC, BD giao nhau tại trung điểm O mỗi đường, hay $A O = C O = \frac{A C}{2}$

Xét tam giác ABD có BE, AO là đường trung tuyến cắt nhau tại K nên K là trọng tâm ΔABD.

Suy ra $A K = \frac{2}{3} A O = \frac{2}{3} . \frac{1}{2} A C = \frac{1}{3} A C$ (1)

Xét tam giác CBD có DF, CO là hai đường trung tuyến cắt nhau tại I nên I là trọng tâm ΔCBD.

Suy ra $C I = \frac{2}{3} C O = \frac{2}{3} . \frac{1}{2} A C = \frac{1}{3} A C$ (2)

Lại có:

$\begin{array}{l} A K + K I + C I = A C \\ \Rightarrow K I = A C - A K - C I \\ = A C - \frac{1}{3} A C - \frac{1}{2} A C = \frac{1}{3} A C (3) \end{array}$

Từ (1), (2) và (3) suy ra: AK = KI = IC

1 119 lượt xem

Bài trước

Bài sau

30 câu Trắc nghiệm Hình bình hành (có đáp án 2024) – Toán 8 Cánh diều

Giới thiệu

Liên kết

Chính sách

Kết nối

30 câu Trắc nghiệm Hình bình hành (có đáp án 2024) – Toán 8 Cánh diều

CHỌN BỘ SÁCH BẠN MUỐN XEM