30 câu Trắc nghiệm Tính chất đường phân giác của tam giác (có đáp án 2024) – Toán 8 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 4: Tính chất đường phân giác của tam giác đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 4.
Trắc nghiệm Toán 8 Bài 4: Tính chất đường phân giác của tam giác
Câu 1 : Cho tam giác ABC có AB<AC, AD là đường phân giác. Khi đó:
- A
BD<DC
- B
BD>DC
- C
BD=DC
- D
Không so sánh được
Đáp án : A
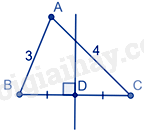
Trong tam giác ABC có AD là đường phân giác của góc BAC nên ABAC=BDDC
Mà AB<AC nên ABAC<1 do đó BDDC<1 nên BD<DC
Câu 2 : Cho hình vẽ:
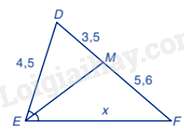
Chọn đáp án đúng
- A
x=12
- B
x=345
- C
x=375
- D
x=365
Đáp án : D
Xét tam giác EDF có EM là tia phân giác của góc FED nên DMMF=EDFE hay 3,55,6=4,5x
x=4,5.5,63,5=365
Câu 3 : Cho tam giác MNP có MN=24cm,MP=32cm. Vẽ MI là đường phân giác của góc M sao cho NI=15cm. Khi đó, IP có độ dài bằng:
- A
10cm
- B
20cm
- C
18cm
- D
22cm
Đáp án : B

Trong tam giác MNP có MI là đường phân giác của góc NMP nên
IPIN=MPMN hay x15=3224 , do đó x=15.3224=20(cm)
Câu 4 : Cho tam giác ABC có AC=2AB , AD là đường phân giác của góc BAC.
Chọn đáp án đúng
- A
BD=34DC
- B
BD=23DC
- C
BD=13DC
- D
BD=12DC
Đáp án : D
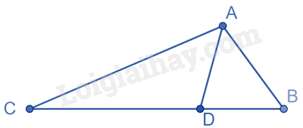
Vì AC=2AB nên ACAB=2
Trong tam giác ABC có AD là đường phân giác của góc BAC nên DCBD=ACAB=2 nên BD=12DC
Câu 5 : Đáp án nào dưới đây có tỉ số BDDC=34 ?
- A
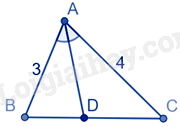
- B

- C
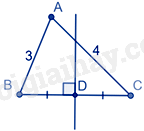
- D
Không có đáp án nào đúng
Đáp án : A
Đáp án A: Xét tam giác ABC có AD là đường phân giác của góc BAC nên ABAC=BDDC=34
Đáp án B, C không đúng.
Câu 6 : Trong tam giác, đường… chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Từ (cụm từ) thích hợp điền vào dấu … để được đáp án đúng là
- A
cao
- B
phân giác của một góc
- C
trung tuyến
- D
trung trực
Đáp án : B
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Câu 7 : Cho tam giác ABC có AD là phân giác trong của góc A. Khi đó,
- A
DCDB=ABAC
- B
DCAC=ABDB
- C
ABBD=DCAC
- D
DCBD=ACAB
Đáp án : D
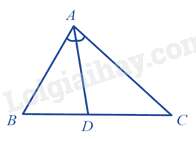
Xét tam giác ABC có AD là đường phân giác của góc BAC nên DCBD=ACAB (tính chất đường phân giác)
Câu 8 : Cho hình vẽ:

Chọn đáp án đúng
- A
xy=715
- B
xy=815
- C
xy=1115
- D
xy=415
Đáp án : A
Xét tam giác ABC có AD là đường phân giác của góc BAC nên BDDC=ABAC , do đó xy=3,57,5=715
Câu 9 : Cho tam giác ABC, D là điểm thuộc đoạn thẳng BC sao cho DBDC=ABAC thì
- A
AD là đường trung tuyến của tam giác ABC
- B
AD là đường phân giác của tam giác ABC
- C
AD là đường trung trực của tam giác ABC
- D
AD là đường cao của tam giác ABC
Đáp án : B
Câu 10 : Cho tam giác ABC có AD là đường phân giác của tam giác. Biết rằng BD=3cm,DC=4cm. Khi đó, tỉ số ABAC bằng:
- A
45
- B
54
- C
34
- D
43
Đáp án : C
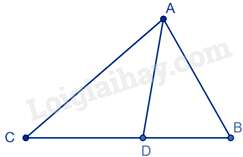
Xét tam giác ABC có AD là đường phân giác của góc BAC nên ABAC=BDDC=34
Câu 11 : Cho tam giác ABC có AD là đường phân giác của tam giác sao cho BD=13BC. Tỉ số ABAC bằng
- A
12
- B
2
- C
3
- D
13
Đáp án : A
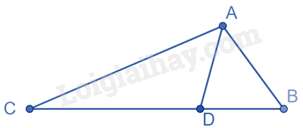
Vì BD=13BC nên DCBD=2
Trong tam giác ABC có AD là đường phân giác của góc BAC nên ACAB=DCBD=2 nên ABAC=12
Câu 12 : Cho hình vẽ sau:
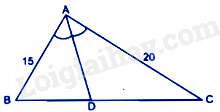
Tỉ số diện tích tam giác ABD và tam giác ADC là:
- A
SABDSADC=56
- B
SABDSADC=45
- C
SABDSADC=23
- D
SABDSADC=34
Đáp án : D
Vì hai tam giác ADC và ADB có cùng đường cao xuất phát từ đỉnh A xuống BC.
Do đó, SABDSADC=BDDC
Trong tam giác ABC có AD là đường phân giác của góc BAC nên BDDC=ABAC=1520=34
Vậy SABDSADC=34
Câu 13 : Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E.
Chọn đáp án đúng.
- A
ECEA=13.DMDA
- B
ECEA=3DMDA
- C
ECEA=2DMDA
- D
ECEA=12.DMDA
Đáp án : C
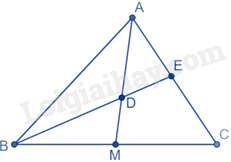
Xét tam giác ABC có BE là đường phân giác của góc ABC nên ECEA=BCBA (1)
Xét tam giác ABM có DB là đường phân giác của góc ABM nên DMDA=BMBA (2)
Mà M là trung điểm của BC nên BM=MC=12BC⇒DMDA=BMBA=BC2.BA
Nên 2DMDA=BCBA (3)
Từ (1), (2) và (3) ta có: ECEA=2DMDA .
Câu 14 : Cho tam giác ABC vuông tại A có AB=4cm,BC=5cm. Vẽ AD là phân giác của góc BAC. Tỉ số DBDC là:
- A
2
- B
53
- C
43
- D
32
Đáp án : C
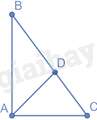
Áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có: AB2+AC2=BC2
AC2=BC2−AB2=16 nên AC=3cm
Trong tam giác ABC có AD là đường phân giác của góc BAC nên BDDC=ABAC=43
Câu 15 : Cho tam giác ABC có BC=10cm. Vẽ AD là tia phân giác của góc BAC sao cho BD=4cm. Tỉ số ABAC là:
- A
45
- B
78
- C
34
- D
23
Đáp án : D
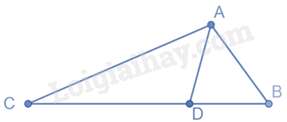
Ta có: CD=BC−CD=6cm
Tam giác ABC có AD là phân giác của góc BAC nên ABAC=DBDC=46=23
Câu 16 : Cho tam giác ABC vuông tại A, có AB=3cm,AC=4cm,AD là đường phân giác. Khoảng cách từ điểm D đến đường thẳng AC là:
- A
1249cm
- B
127cm
- C
137cm
- D
1349cm
Đáp án : B
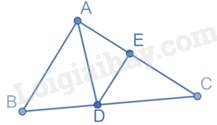
Kẻ DE vuông góc với AC tại E, khi đó DE là khoảng cách từ D đến AC
Lại có: AB vuông góc với AC nên DE//AB
Áp dụng định lý Pytago vào tam giác ABC vuông tại A có: BC2=AB2+AC2=25 nên BC=5cm
Xét tam giác ABC có AD là đường phân giác của góc BAC nên BDDC=ABAC=34 nên BD=34DC
Ta có: BD+DC=BC
34DC+DC=5 nên DC=207cm
Tam giác ABC có DE//AB nên theo hệ quả của định lý Thalès ta có:
DEAB=DCBC hay DE3=2075=47 nên DE=47.3=127(cm)
Vì AD là đường phân giác của góc BAC nên ^DAE=12^BAC=450
Mà tam giác DAE vuông tại E nên tam giác DAE vuông cân tại E. Do đó, DE=AE=127cm
Câu 17 : Cho hình vẽ:
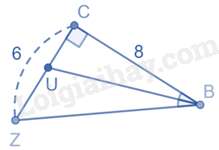
Độ dài đoạn thẳng UC là:
- A
83
- B
3
- C
103
- D
Đáp án khác
Đáp án : A
Tam giác BCZ vuông tại C nên theo định lý Pytago ta có:
BZ=√BC2+CZ2=10
Trong tam giác BCZ có BU là đường phân giác của góc CBZ nên UCUZ=BCBZ=810=45
Do đó, UC4=UZ5
Theo tính chất của dãy tỉ số bằng nhau ta có:
UC4=UZ5=UC+UZ4+5=CZ9=69=23 nên UC=4.23=83
Câu 18 : : Cho tam giác ABC vuông tại A có AB=15cm,AC=20cm , đường cao AH (H thuộc BC). Tia phân giác của góc HAB cắt HB tại D. Tia phân giác của góc HAC cắt HC tại E. Độ dài đoạn thẳng DH bằng:
- A
4cm
- B
6cm
- C
9cm
- D
12cm
Đáp án : A
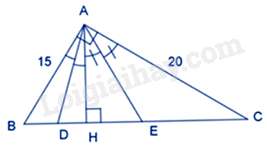
Áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có: BC2=AB2+AC2=625 nên BC=25cm
Diện tích tam giác ABC là: SABC=12AB.AC=12AH.BC nên AH=AB.ACBC=15.2025=12(cm)
Áp dụng định lý Pytago vào tam giác AHB vuông tại H có: AB2=AH2+HB2
HB2=AB2−AH2=81 nên HB=9cm , do đó, HC=BC−HB=16(cm)
Vì AD là đường phân giác của góc BAH trong tam giác ABH nên
ABAH=BDDH=BH−DHDH nên 1512=9−DHDH
15DH=108−12DH nên DH=4cm
Câu 19 : Cho tam giác ABC cân tại A, đường phân giác của góc ABC cắt AC tại D và AB=15cm,BC=10cm. Khi đó, độ dài đoạn thẳng AD bằng
- A
3cm
- B
6cm
- C
9cm
- D
12cm
Đáp án : C
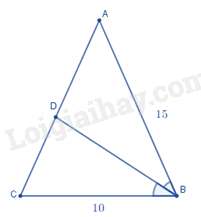
Vì tam giác ABC cân tại A nên AB=AC=15cm
Xét tam giác ABC có BD là đường phân giác của góc ABC nên ADDC=ABBC , do đó ADAD+DC=ABBC+AB hay ADAC=ABBC+AB , do đó AD15=1515+10
Suy ra: AD=15.1525=9(cm)
Câu 20 : Cho tam giác ABC có chu vi 27cm, các đường phân giác BD và CE. Biết rằng ADDC=12,AEEB=34 . Chọn đáp án đúng.
- A
AB=12cm,BC=9cm,AC=6cm
- B
AB=6cm,BC=12cm,AC=9cm
- C
AB=6cm,BC=9cm,AC=12cm
- D
AB=12cm,BC=6cm,AC=9cm
Đáp án : B

Vì BD, CE là các đường phân giác trong tam giác ABC nên:
ABBC=ADDC=12;ACBC=AEEB=34
Do đó AB2=BC4=AC3
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: AB2=BC4=AC3=AB+BC+AC2+4+3=279=3
Do đó, AB=6cm,BC=12cm,AC=9cm
Câu 21 : : Cho tam giác ABC với đường trung tuyến AM và phân giác AD. Biết rằng AB=m,AC=n(n>m) . Diện tích tam giác ADM là:
- A
SAMD=n+m3(m−n)SABC
- B
SAMD=n−m3(m+n)SABC
- C
SAMD=n+m2(m−n)SABC
- D
SAMD=n−m2(m+n)SABC
Đáp án : D

Vì tam giác ADM và tam giác ABC có chung chiều cao kẻ từ A đến BC nên SADMSABC=DMBC⇒SADM=DMBC.SABC
Xét tam giác ABC có AD là đường phân giác của góc BAC nên: DBDC=BACA=mn⇒DB=mt,DC=nt (với t>0 )
Do đó, BC=DC+BD=(m+n)t , suy ra BM=12BC=(m+n)t2
Ta có: DM=BM−DB=(m+n)t−2mt2=(n−m)t2
Suy ra: DMBC=(n−m)t2(m+n)t=n−m2(m+n)
Vậy SAMD=n−m2(m+n)SABC
Câu 22 : Cho hình bình hành ABCD có AB=a=12,5cm,BC=b=7,25cm. Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F. Biết rằng FE=m=3,45cm .
Chọn đáp án đúng
- A
AC≈12,98cm
- B
AC≈12,97cm
- C
AC≈12,88cm
- D
AC≈12,87cm
Đáp án : A
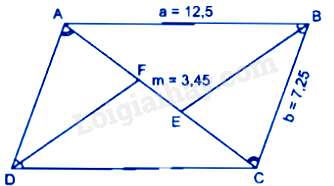
Vì ABCD là hình bình hành nên ^ABC=^ADC.
Vì BE và DF lần lượt là phân giác của góc ABC và góc ADC nên ^ADF=^CBE
Mặt khác, ta có: AD=CB=b,^DAF=^BCE (so le trong)
Suy ra: ΔADF=ΔCBE(g.c.g) nên AF=CE
Đặt AF=CE=x
Xét tam giác ABC có BE là đường phân giác của góc ABC nên
ABBC=AECE=FA+FECE⇒ab=x+mx⇒x=mba−b
AC=2x+m=2mba−b+m=m(a+b)a−b=3,45(12,5+7,25)12,5−7,25≈12,98cm
Câu 23 : Cho tam giác ABC có AB=4cm,AC=5cm,BC=6cm , các đường phân giác BD, CE cắt nhau tại I. Tỉ số diện tích của các tam giác ADE và ABC là:
- A
SADESABC=311
- B
SADESABC=211
- C
SADESABC=411
- D
SADESABC=511
Đáp án : B
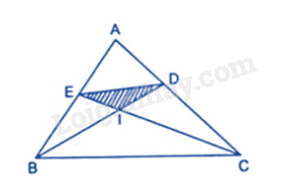
Tam giác ABC có BD là đường phân giác của góc ABC nên DADC=ABBC=46=23⇒AD=23DC
Lại có: AC=DC+AD=23DC+DC=53DC⇒53DC=5⇒DC=3cm⇒AD=2cm
Vì tam giác DAE và tam giác CAE có chung đường cao kẻ từ E đến AC nên SDAESACE=ADAC=25(1)
Vì tam giác ACE và tam giác CAB có chung đường cao kẻ từ C đến AB nên SACESABC=AEAB(2)
Tam giác ABC có CE là đường phân giác của góc ACB nên:
AEEB=ACBC⇒AEAC=EBBC hay AE5=EB6
Theo tính chất của dãy tỉ số bằng nhau ta có: AE5=EB6=AE+EB5+6=AB11=411
Suy ra: AE=411.5=2011⇒AEAB=511(3)
Thay (3) vào (2) ta có: SACESABC=511(4)
Nhân vế với vế của (1) và (4) ta có: SADESABC=25.511=211
Câu 24 : Cho tam giác ABC có AB=8cm,AC=12cm, đường phân giác AD. Trên đoạn AD lấy điểm E sao cho AEAD=35. Gọi K là giao điểm của BE và AC. Tính tỉ số AKKC
- A
35
- B
34
- C
37
- D
47
Đáp án : A

Kẻ DI//BK thì DI//EK
Áp dụng định lý Thalès vào tam giác AID và tam giác BKC ta được: AKKI=AEED=32 ⇒AK=3KI2(1);CKKI=CBBD(2)
Tam giác ABC có AD là đường phân giác của góc BAC nên DCDB=CAAB hay CDDB=128=32⇒CD3=DB2
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: CD3=DB2=CD+DB2+3=BC5⇒CBDB=52(3)
Thay (3) vào (2) ta có: CKKI=52⇒CK=52KI(4)
Chia theo vế các đẳng thức của (1) và (4) ta được: AKKC=3KI2:5KI2=35
Câu 25 : Cho tam giác ABC có AB=c,AC=b,BC=a, các đường phân giác AD, BE, CF cắt nhau ở I. Chọn đáp án đúng
- A
DIDA+EIEB+FIFC=12
- B
DIDA+EIEB+FIFC=2
- C
DIDA+EIEB+FIFC=1
- D
Đáp án khác
Đáp án : C
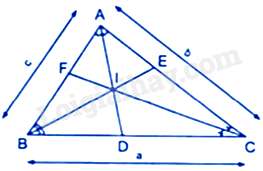
Áp dụng tính chất của đường phân giác AD và BI vào các tam giác ABC, ABD ta được: DIIA=DBBA=DBc(1)
DBBA=DCCA hay DBc=DCb
Theo tính chất của dãy tỉ số bằng nhau ta có: DBc=DCb=DB+DCc+b=BCb+c⇒DB=cab+c(2)
Thay (2) vào (1) ta được: DIIA=cac(b+c)=ab+c
Suy ra: DIa=IAb+c=DI+IAa+b+c=ADa+b+c⇒DIAD=aa+b+c(3)
Chứng minh tương tự ta có: EIEB=ba+b+c,FIFC=ca+b+c(5)
Cộng theo vế của (3), (4), (5) ta có: DIDA+EIEB+FIFC=a+b+ca+b+c=1
Câu 26 : Cho hình vẽ:
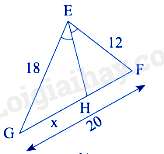
Chọn đáp án đúng.
- A
x=13
- B
x=12
- C
x=14
- D
Cả A, B, C đều sai
Đáp án : B
Ta có: HF=GF−GH=20−x
Xét tam giác GEF có EH là đường phân giác của góc GEF nên
GHHF=EGFE hay x20−x=1812
12x=18(20−x)
12x=360−18x
30x=360
x=12
Câu 27 : Cho tam giác ABC có AB=2,BC=3,CA=4 , AD là đường phân giác và I là giao điểm của ba đường phân giác của tam giác đó. Tính tỉ số IDIA
- A
56
- B
13
- C
12
- D
34
Đáp án : C
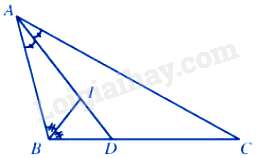
Trong tam giác ABC có AD là đường phân giác của góc BAC nên BDDC=ABAC=24=12 nên DB1=DC2
Theo tính chất của dãy tỉ số bằng nhau ta có: DB1=DC2=DB+DC1+2=BC3=33=1
Do đó, DB=1
Xét tam giác ABD có BI là đường phân giác của góc ABD nên IDIA=BDBA=12
Câu 28 : Cho tam giác ABC có ba đường phân giác AD, BE, CF. Khi đó:
- A
DBDC.ECEA.FAFB=12
- B
DBDC.ECEA.FAFB=1
- C
DBDC.ECEA.FAFB=2
- D
DBDC.ECEA.FAFB=13
Đáp án : B

Xét tam giác ABC có:
AD là đường phân giác của góc BAC nên BDDC=ABAC
BE là đường phân giác của góc ABC nên ECEA=BCAB
CF là đường phân giác của góc BCA nên FAFB=ACBC
Do đó, DBDC.ECEA.FAFB=ABAC.BCAB.ACBC=1
Câu 29 : Cho tam giác ABC có AM là đường trung tuyến. Gọi MD, ME lần lượt là đường phân giác của các tam giác AMB và AMC. Gọi I là giao điểm của DE và AM.
Chọn đáp án đúng.
- A
DI=45DE
- B
DI=34DE
- C
DI=23DE
- D
DI=DE
Đáp án : D
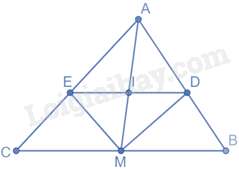
Xét tam giác AMB có MD là đường phân giác của góc AMB nên DADB=MAMB
Xét tam giác AMC có ME là đường phân giác của góc AMC nên EAEC=MAMC
Mà MB=MC nên MAAB=MAMC nên DADB=EAEC , do đó DE//BC (định lý Thalès đảo)
Áp dụng hệ quả của định lý Thalès vào hai tam giác ABM và ACM có:
IDMB=IAAM và IEMC=AIAM , do đó, IDMB=IEMC
Mà MB=MC nên DI=DE
Câu 30 : Cho tam giác ABC có BA=BC=a,AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Tính MN
- A
MN=2aba+b
- B
MN=aba+b
- C
MN=ab2(a+b)
- D
MN=aba+b
Đáp án : B
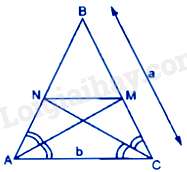
Xét tam giác ABC có AM là đường phân giác góc BAC nên MBMC=ABAC=ab
Xét tam giác ABC có CN là đường phân giác góc BCA nên NBNA=CBAC=ab
Do đó, NBNA=MBMC nên MN//AC (định lý Thalès đảo)
Ta có: NBNA=CBAC=ab⇒NBNB+NA=aa+b hay NBAB=aa+b
Do đó, NB=a2a+b
Lại có: MN//AC nên MNAC=NBAB , do đó MN=AC.NBAB=aba+b