30 câu Trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác (có đáp án 2024) – Toán 8 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 8: Trường hợp đồng dạng thứ ba của tam giác đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 8.
Trắc nghiệm Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác
Câu 1 : Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng HB=7cm,HC=18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
- A
CE=15cm
- B
CE=16cm
- C
CE=12cm
- D
CE=10cm
Đáp án : A
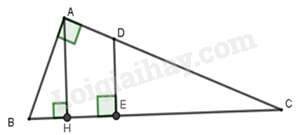
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Tam giác AHC và tam giác ABC có: ^AHC=^BAC=900,ˆCchung. Do đó, ΔACH∽ΔBCA
Ta có: SDEC=12SABC(1) , SAHCSABC=12HC.AH12BC.AH=HCBC=1825⇒SAHC=1825SABC(2)
Từ (1) và (2) ta có: SDEC:SAHC=12:1825=2536=(56)2(3)
Tam giác DEC và tam giác AHC có: ^DEC=^AHC=900,ˆCchung
ΔDEC∽ΔAHC⇒SDECSAHC=(ECHC)2(4)
Từ (3) và (4) ta có: ECHC=56 ⇒ EC18=56⇒EC=15cm
Câu 2 : Cho hình bình hành ABCD (AC>AB) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD và H là hình chiếu của B trên AC.
Chọn đáp án đúng.
- A
AB.AE+AD.AK=2AC2
- B
2AB.AE+AD.AK=AC2
- C
AB.AE+2AD.AK=AC2
- D
AB.AE+AD.AK=AC2
Đáp án : D
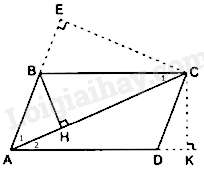
Tam giác AHB và tam giác AEC có: ^A1chung,^AHB=ˆE=900
Do đó, ΔAHB∽ΔAEC⇒AHAE=ABAC⇒AB.AE=AC.AH
Vì BC// AD (do ABCD là hình bình hành) nên ^C1=^A2 , mà ^BHC=ˆK=900
Do đó, ΔAKC∽ΔCHB⇒AKCH=ACCB⇒AK.CB=AC.CH
Vì ABCD là hình bình hành nên BC=AD
Do đó, AD.AK=AC.CH(3)
Từ (1), (2) và (3) ta có:
AB.AE+AD.AK=AC(AH+CH)=AC2
Câu 3 : Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
- A
BM.BD+CM.CA=12BC2
- B
BM.BD+2CM.CA=BC2
- C
BM.BD+CM.CA=BC2
- D
BM.BD+CM.CA=2BC2
Đáp án : C

Kẻ MI vuông góc với BC tại I
Tam giác BIM và tam giác BDC có: ^BIM=^BDC=900,^MBCchung
Do đó, ΔBIM∽ΔBDC⇒BMBC=BIBD⇒BM.BD=BC.BI(1)
Chứng minh tương tự ta có: ΔICM∽ΔACB⇒CMBC=CICA⇒CM.CA=BC.CI(2)
Từ (1) và (2) ta có: BM.BD+CM.CA=BC.BI+BC.CI=BC(BI+CI)=BC2
Câu 4 : Cho tam giác ABC cân tại A, AC=20cm,BC=24cm. Các đường cao AD và CE cắt nhau tại H. Khi đó,
- A
HD=12cm
- B
HD=6cm
- C
HD=9cm
- D
HD=10cm
Đáp án : C
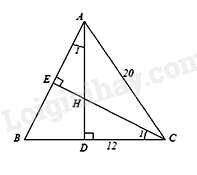
Tam giác ABC cân tại A nên BD=DC=BC2=12(cm)
Áp dụng định lý Pytago vào tam giác ADC vuông tại D ta có: AD2=AC2−DC2=162⇒AD=16cm
Tam giác CDH và tam giác ADB có: ^CDH=^ADB=900,^C1=^A1 (cùng phụ với góc B)
Do đó, ΔCDH∽ΔADB⇒HDBD=CDAD⇒HD12=1216=34
Suy ra: HD=9cm
Câu 5 : Cho tam giác ABC cân tại A, đường cao CE. Biết rằng BE=3cm,BC=8cm.
Độ dài đoạn thẳng AB là:
- A
343cm
- B
32cm
- C
323cm
- D
35cm
Đáp án : C
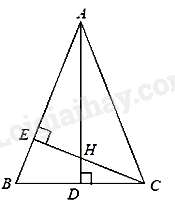
Kẻ đường cao AD của tam giác ABC.
Vì tam giác ABC cân tại A nên AD là đường cao đồng thời là đường trung tuyến
Suy ra: BD=12BC=4cm
Xét tam giác CBE và tam giác ABD có: ^BEC=^ADB=900 và góc B chung
Do đó, ΔCBE∽ΔABD(g.g)⇒BCAB=BEBD⇒AB=BD.BCBE=323(cm)
Câu 6 : Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
- A
2AC=CH.BC
- B
AC2=12CH.BC
- C
AC2=CH.BC
- D
AC2=2CH.BC
Đáp án : C
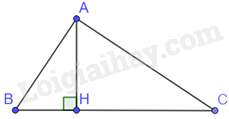
Tam giác ACH và tam giác CBA có: ^AHC=^BAC=900,ˆCchung
Do đó, ΔACH∽ΔBCA(g.g)⇒ACBC=CHAC⇒AC2=CH.BC
Câu 7 : Cho tam giác ABC cân tại A , đường cao CE . Tính AB , biết BC=24 cm và BE=9 cm.
- A
16cm
- B
32cm
- C
24cm
- D
18cm
Đáp án : B
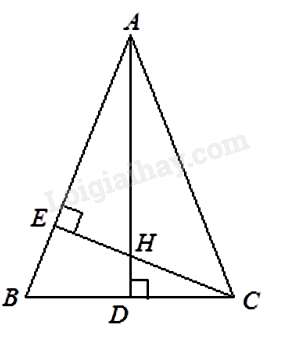
Kẻ đường cao AD . Xét ΔCBE và ΔABD có ^BEC=^ADB=90∘ và ˆB chung nên ΔCBE∽ΔABD⇒BCAB=BEBD hay 24AB=912
⇒AB=32cm .
Câu 8 : Cho hình vẽ:
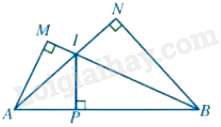
Chọn đáp án đúng
- A
AI.AN+BI.BM=2AB2
- B
AI.AN+BI.BM=AB2
- C
AI.AN+2BI.BM=AB2
- D
2AI.AN+BI.BM=AB2
Đáp án : B
Tam giác ABN và tam giác AIP có: ˆN=^IPA=900,^BANchung
Do đó, ΔABN∽ΔAIP⇒ABAI=ANAP⇒AI.AN=AP.AB
Tam giác AMB và tam giác IPB có: ˆM=^IPB=900,^ABMchung
Do đó, ΔAMB∽ΔIPB⇒ABBI=BMBP⇒AB.BP=BI.BM
Vậy AI.AN+BI.BM=AP.AB+AB.PB=AB(AP+PB)=AB2
Câu 9 : Cho hình vẽ:
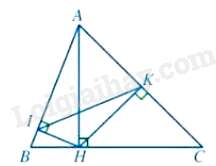
Chọn đáp án đúng
- A
AC.AK=12AB.AI
- B
AC.AK=2AB.AI
- C
AC.AK=3AB.AI
- D
AC.AK=AB.AI
Đáp án : D
Tam giác AHI và tam giác ABH có: ^HAIchung,^AIH=^AHB=900
Do đó, ΔAHI∽ΔABH⇒AHAB=AIAH⇒AH2=AB.AI (1)
Tam giác AHK và tam giác ACH có: ^HACchung, ^AKH=^AHC=900
Do đó, ΔAHK∽ΔACH⇒AHAC=AKAH⇒AH2=AK.AC (2)
Từ (1) và (2) ta có: AC.AK=AB.AI
Câu 10 : Cho hình vẽ:
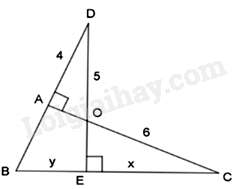
Chọn đáp án đúng.
- A
y=10
- B
x=4,8
- C
A, B đều đúng
- D
A, B đều sai
Đáp án : B
Tam giác ADO và tam giác ECO có: ^DAO=^CEO=900,^AOD=^COE (hai góc đối đỉnh)
Do đó, ΔADO∽ΔECO⇒ADEC=DOCO⇒4x=56⇒x=4,8
Áp dụng định lý Pytago vào tam giác ADO vuông tại A ta có:
AD2+AO2=OD2 ⇒AO2=DO2−AD2=9⇒AO=3
Tam giác CEO và tam giác CAB có: ^CEO=^CAB=900,ˆCchung
Do đó, ΔCEO∽ΔCAB⇒COCB=CECA⇒COEC+EB=CECO+AO⇒64,8+y=4,86+3⇒y=6,45
Câu 11 : Cho tam giác ABC vuông tại A có ˆB=300, tam giác MNP vuông tại M có ˆN=600.
Chọn đáp án đúng.
- A
AB.PN=MP.BC
- B
AB.MP=PN.BC
- C
AB.MP=2PN.BC
- D
AB.PN=2MP.BC
Đáp án : A
Tam giác ABC vuông tại A nên ˆB+ˆC=900⇒ˆC=900−ˆB=600
Tam giác ABC và tam giác MNP có: ˆA=ˆM=900,ˆC=ˆN(=600)
Do đó, ΔABC∽ΔMPN(g.g)⇒ABMP=BCPN⇒AB.PN=MP.BC
Câu 12 : Cho hình vẽ:
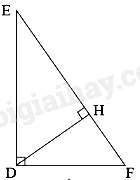
Khẳng định nào sau đây là đúng?
- A
DH2=HE+2HF
- B
DH2=HE.HF
- C
DH2=HE+HF
- D
DH2=HE−HF
Đáp án : B
Ta có: ^EDH+^HDF=ˆF+^HDF(=900)⇒^EDH=ˆF
Tam giác EDH và tam giác DFH có:
^EHD=^FHD=900,^EDH=ˆF
Do đó, ΔEDH∽ΔDFH(g.g) nên DHFH=EHDH⇒DH2=EH.FH
Câu 13 : Một ngọn tháp cho như hình vẽ dưới đây, biết rằng MB=20m,MF=2m,FE=1,65m.
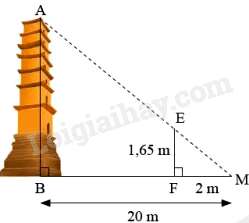
Chiều cao AB của ngọn tháp bằng:
- A
17,5m
- B
14,5m
- C
16,5m
- D
15,5m
Đáp án : C
Xét tam giác AMB và tam giác EMF có:
^ABM=^EFM=900,ˆMchung
Do đó, ΔABM∽ΔEFM(g.g)
Suy ra: ABFE=BMFM=202=10⇒AB=10.FE=10.1,65=16,5(m)
Câu 14 : Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM=2m,AM⊥AB và đo được góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A’M’B’ vuông tại A’ có A′M′=1cm,^A′M′B′=^AMB và đo được A′B′=5cm (hình vẽ dưới). Khoảng cách từ A đến B bằng:

- A
4m
- B
6m
- C
8m
- D
10m
Đáp án : D
Đổi 1cm=0,01m;5cm=0,05m
Tam giác AMB và tam giác A’M’B’ có: ^BAM=^B′A′M′=900,^AMB=^A′M′B′
Do đó,ΔAMB∽ΔA′M′B′(g.g)
Suy ra, ABA′B′=AMA′M′=20,01=200⇒AB=200.A′B′=10(m)
Câu 15 : Cho hình vẽ:
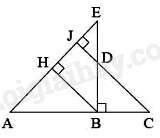
Chọn đáp án đúng.
- A
BCBE=2BDBA
- B
BCBE=BDBA
- C
2BCBE=BDBA
- D
A, B, C đều sai
Đáp án : B
Ta có: ˆA+ˆC=ˆA+ˆE(=900)⇒ˆC=ˆE
Xét tam giác ABE và tam giác DCB có: ^ABE=^DBC=900,ˆE=ˆC
Do đó, ΔABE∽ΔDBC(g.g)
Do đó, BCBE=BDBA
Câu 16 : Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
- A
ΔACH∽ΔBCA
- B
ΔACH∽ΔCBA
- C
ΔACH∽ΔBAC
- D
ΔACH∽ΔCBA
Đáp án : A
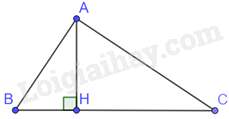
Tam giác ACH và tam giác CBA có: ^AHC=^BAC=900,ˆCchung
Do đó, ΔACH∽ΔBCA(g.g)
Câu 17 : Cho các mệnh đề sau. Chọn câu đúng.
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- A
(I) đúng, (II) sai
- B
(I) sai, (II) đúng
- C
(I) và (II) đều sai
- D
(I) và (II) đều đúng
Đáp án : A
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Vậy (I) đúng, (II) sai.
Câu 18 : Cho tam giác ABC vuông tại A và DEF vuông tại D. Để ΔABC∽ΔDEF thì ta cần thêm điều kiện:
- A
ˆB=ˆE
- B
ˆB=ˆF
- C
ˆB=12ˆE
- D
ˆB=12ˆF
Đáp án : A
Điều kiện cần thêm là: ˆB=ˆE
Câu 19 : Cho hình vẽ:
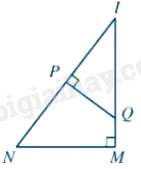
Chọn đáp án đúng
- A
ΔIPQ∽ΔIMN
- B
ΔIPQ=ΔIMN
- C
ΔIPQ∽ΔINM
- D
ΔIPQ∽ΔMNI
Đáp án : A
Lời giải:
Do đó, ΔIPQ∽ΔIMN(g.g)
Câu 20 : Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: ˆB=ˆF
Chọn đáp án đúng
- A
ΔABC=ΔDEF
- B
ΔABC∽ΔDFE
- C
ΔABC∽ΔEDF
- D
ΔABC∽ΔDEF
Đáp án : B
Tam giác ABC và tam giác DEF có: ^BAC=^EDF=900,ˆB=ˆF nên ΔABC∽ΔDFE(g.g)
Câu 21 : Nếu ΔMNP và ΔDEF có ˆM=ˆD=90∘ , ˆP=50∘ . Để ΔMNP∽ΔDEF thì cần thêm điều kiện
- A
ˆE=50∘ .
- B
ˆF=60∘ .
- C
ˆF=40∘ .
- D
ˆE=40∘
Đáp án : D
ΔMNP có ˆM=90∘ , ˆP=50∘ ⇒ˆN=40∘ .
ΔMNP và ΔDEF có ˆM=ˆD (gt) cần thêm điều kiện ˆE=40∘ thì ⇒ˆN=ˆE=40∘
Lúc này ΔMNP∽ΔDEF (g – g ).
Câu 22 : Nếu ΔDEF và ΔSRK có ˆD=70∘ ; ˆE=60∘ ; ˆS=70∘ ; ˆK=50∘ thì
- A
DESR=DFSK=EFRK .
- B
DESR=DFRK=EFSK .
- C
DESR=DFSR=EFRK .
- D
DERK=DFSK=EFSR
Đáp án : A
ΔDEF có ˆD+ˆE+ˆF=180∘⇒70∘+60∘+ˆF=180∘⇒ˆF=50∘ .
ΔDEF và ΔSRK có ˆD=ˆS=70∘ và ˆF=ˆK=50∘ nên ΔDEF∽ΔSRK (g – g).
Suy ra DESR=DFSK=EFRK .
Câu 23 : Cho hình vẽ. Khẳng định nào sao đây đúng
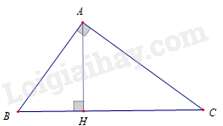
- A
ΔABC∽ΔABH .
- B
ΔABC∽ΔHAB .
- C
ΔABC∽ΔAHB .
- D
ΔABC∽ΔHBA .
Đáp án : D
ΔABC và ΔHBA có góc ˆB chung, ^BAC=^AHB=90∘ nên ΔABC∽ΔHBA (g – g)
Câu 24 : Cho ΔABC vuông tại A, đường cao AH. Hệ thức nào sau đây đúng?
- A
AB=BC.BH.
- B
AC2=CH.BH.
- C
AH2=BH.CH.
- D
AH=CH.BH.
Đáp án : C
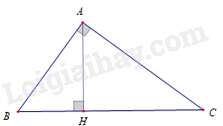
Xét ΔHCA và ΔHAB có:
^HAC=ˆB (Vì cùng phụ với ^HAB ); ^CHA=^AHB=90∘
nên ΔHCA∽ΔHAB (g – g ) ⇒AHBH=CHAH⇔AH2=BH.CH.
Câu 25 : Cho hình thang ABCD (AB//CD), O là giao điểm hai đường chéo AC và BD. Khẳng định nào sau đây đúng
- A
ΔOAB∽ΔODC.
- B
ΔCAB∽ΔCDA.
- C
ΔOAB∽ΔOCD.
- D
ΔOAD∽ΔOBC.
Đáp án : C
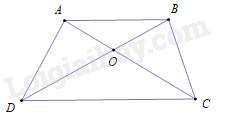
Vì AB//CD (gt) nên ^ABO=^ODC (cặp góc so le trong) .
ΔOAB và ΔOCD có:
^ABO=^ODC (chứng minh trên); ^AOB=^COD (hai góc đối đỉnh)
Nên ΔOAB∽ΔOCD (g – g ).
Câu 26 : Cho hình thang ABCD (AB//CD), O là giao điểm hai đường chéo AC và BDKhẳng định nào sau đây đúng
- A
OA.OC=OB.OD.
- B
OA.OD=OB.OC.
- C
OA.OB=OC.OD.
- D
OA.AB=OC.CD.
Đáp án : B
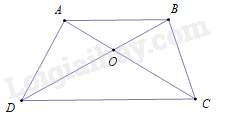
Vì AB//CD (gt) nên ^ABO=^ODC (cặp góc so le trong) .
ΔOAB và ΔODC có:
^ABO=^ODC (chứng minh trên); ^AOB=^COD (hai góc đối đỉnh)
Nên ΔOAB∽ΔOCD (g – g ) ⇒OAOC=OBOD⇔OA.OD=OB.OC.
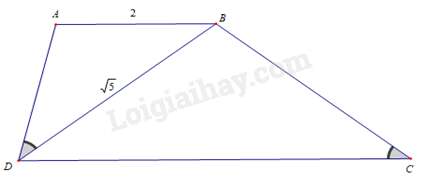
Câu 27 : Cho hình thang ABCD(AB//CD), ^ADB=^BCD, AB=2cm, BD=√5cm. Độ dài đoạn thẳng CD là
- A
2√5cm.
- B
√5−2cm.
- C
√52cm.
- D
2,5cm.
Đáp án : D
Vì AB//CD⇒^ABD=^BDC (cặp góc so le trong).
Xét ΔADB và ΔBCD có:
^ABD=^BDC (chứng minh trên); ^ADB=^BCD (gt)
Nên ΔADB∽ΔBCD (g – g ).
⇒ABBD=DBCD⇔2√5=√5CD⇔CD=√5.√52=52=2,5(cm).
Câu 28 : Cho hình thang vuông ABCD, (ˆA=ˆD=90∘) có DB⊥BC, AB=4cm, CD=9cm. Độ dài đoạn thẳng BD là
- A
8cm.
- B
12cm.
- C
9cm.
- D
6cm.
Đáp án : d
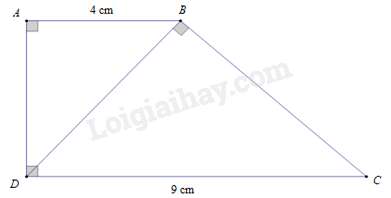
Ta có AB//CD ( vì cùng vuông góc với AD).⇒^ABD=^BDC (cặp góc so le trong)
Xét ΔABD và ΔBDC có:
^BAD=^DBC=90∘; ^ABD=^BDC (chứng minh trên)
Nên ΔABD∽ΔBDC (g – g) ⇒ABBD=BDDC⇒BD2=AB.DC=4.9=36⇒BD=6(cm).
Câu 29 : Cho ΔABC vuông tại A, đường cao AH biết BH=4cm, CH=9cm. Độ dài đoạn thẳng AH là
- A
4,8cm.
- B
5cm.
- C
6cm.
- D
36cm.
Đáp án : C
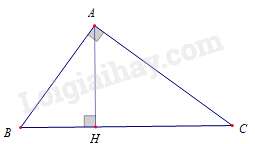
Xét ΔHCA và ΔHAB có :
^HAC=ˆB (Vì cùng phụ với ^HAB) ; ^CHA=^AHB=90∘
nên ΔHCA∽ΔHAB (g – g ) ⇒AHBH=CHAH⇔AH2=BH.CH .
⇔AH2=4.9=36⇒AH=6(cm) .
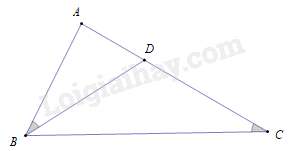
Câu 30 : Cho hình vẽ, biết ^ACB=^ABD, AB=3cm, AC=4,5cm. Độ dài đoạn thẳng AD là
- A
2cm.
- B
2,5cm.
- C
3cm.
- D
1,5cm.
Đáp án : A
Xét ΔABC và ΔADB có:
Góc A chung, ^ACB=^ABD (gt)
Nên ΔABC∽ΔADB (g– g ) ⇒ABAD=ACAB⇔AD=AB.ABAC=3.34,5=2(cm)
Câu 31 : Cho ΔABC vuông tại A có AB=30cm, AC=40cm. Kẻ đường cao AH(H∈BC). Độ dài đường cao AH là
- A
18cm.
- B
24cm.
- C
32cm.
- D
36cm.
Đáp án : B
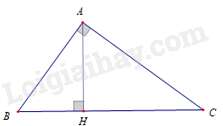
ΔABC vuông tại A nên BC=√AB2+AC2=√302+402=√2500=50(cm).
ΔABC và ΔHBA có góc B chung, ^BAC=^AHB=90∘ nên ΔABC∽ΔHBA (g – g ).
⇒ACAH=BCAB⇔40AH=5030⇔AH=40.3050=24(cm).
Câu 32 : ΔABC cân tại A, hai đường cao AH và BK, cho BC=6cm, AB=5cm. Độ dài đoạn thẳng BK là
- A
4,5cm.
- B
4,8cm.
- C
3cm.
- D
4cm.
Đáp án : B
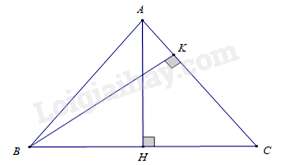
Ta có ΔABC cân tại A ⇒AC=AB=5(cm).
Vì ΔABC cân tại A nên AH là đường cao đồng thời là đường trung tuyến ứng với cạnh BC ⇒HB=HC=BC2=62=3(cm).
Áp dụng định lí Pytago vào tam giác vuông ABH ta có:
AH2=AB2−HB2=52−32=16 ⇒AH=4(cm)
Xét ΔAHC và ΔBKC có: góc C chung; ^AHC=^BKC=90∘.
Nên ΔAHC∽ΔBKC ( g – g )⇒AHBK=CACB⇔BK=AH.CBCA=4.65=4,8(cm).
Câu 33 : ΔABC vuông tại A có ˆB=60∘, BD là phân giác ˆB, AC=18cm. Độ dài đoạn thẳng BD là
- A
12cm.
- B
10cm.
- C
9cm.
- D
8cm.
Đáp án : A
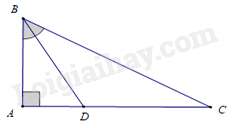
ΔABC có ˆA=90∘ nên ˆB+ˆC=90∘⇒^ACB=30∘.
Vì BD là phân giác của ˆB nên ^ABD=^DBC=12^ABC=30∘.
Xét ΔABC và ΔADB có: ^ACB=^ABD=30∘; ˆA chung
Nên ΔABC∽ΔADB ( g – g ) ⇒BCBD=ACAB⇔BD=AB.BCAC.
Xét ΔABC có ˆA=90∘, ˆC=30∘ nên ΔABC là nửa tam giác đều ⇒BC=2AB.
Áp dụng định lí Pytago vào ΔABC có:
BC2=AB2+AC2⇔(2AB)2=AB2+182⇔3AB2=324⇔AB=√108cm.
⇒BC=2√108cm. Từ đó BD=AB.BCAC=√108.2√10818=12(cm).
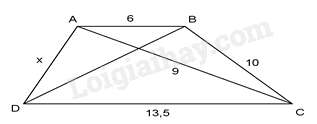
Câu 34 : Với AB//CD thì giá trị của x trong hình vẽ dưới đây là
- A
x = 15
- B
x = 16
- C
x = 7
- D
x = 8
Đáp án : A
Lời giải :
Ta có ABAC=69=23,ACCD=913,5=23
⇒ABAC=ACCD=23
Xét ΔABC và ΔCAD có: ABAC=ACCD(cmt),^BAC=^ACD (so le trong, AB//CD )
⇒ΔABC∽ΔCAD(c−g−c)⇒ABAC=CACD=BCAD=23⇒10x=23⇒x=10.32=15
Câu 35 : Nếu ΔABC và ΔDEF có ˆA=ˆD , ˆC=ˆF thì
- A
ΔABC∽ΔDEF .
- B
ΔCAB∽ΔDEF .
- C
ΔABC∽ΔDFE .
- D
ΔCAB∽ΔDFE
Đáp án : A
Xét ΔABC và ΔDEF có ˆA=ˆD , ˆC=ˆF nên ΔABC∽ΔDEF (g – g)
Câu 36 : Nếu ΔABC và ΔDEF có ˆA=70∘ , ˆC=60∘ , ˆE=50∘ , ˆF=70∘ thì
- A
ΔACB∽ΔFED .
- B
ΔABC∽ΔFED .
- C
ΔABC∽ΔDEF .
- D
ΔABC∽ΔDFE .
Đáp án : B
ΔABC có ˆA+ˆB+ˆC=180∘⇒70∘+ˆB+60∘=180∘⇔ˆB=50∘ .
ΔABC và ΔFED có ˆA=ˆF=70∘ , ˆB=ˆE=50∘ nên ΔABC∽ΔFED (g – g ).
Câu 37 : Nếu ΔABC và ΔFED có ˆA=ˆF ,cần thêm điều kiện gì dưới đây để ΔABC∽ΔFED ?
- A
ˆB=ˆE .
- B
ˆC=ˆE .
- C
ˆB=ˆD .
- D
ˆC=ˆF .
Đáp án : B
ΔABC và ΔFED có ˆA=ˆF , ˆB=ˆE nên ΔABC∽ΔFED (g – g).
Câu 38 : Cho ΔABC∽ΔA′B′C′ (g – g ). Khẳng định nào sau đây đúng
- A
ˆA=^B′ .
- B
AB=A′B′ .
- C
ABAC=A′B′A′C′ .
- D
ABAC=A′C′A′B′ .
Đáp án : B
ΔABC∽ΔA′B′C′⇒ABAC=A′B′A′C′
Câu 39 : Cho hình vẽ, khẳng định nào sau đây đúng

- A
ΔHIG∽ΔDEF .
- B
ΔIGH∽ΔDEF .
- C
ΔHIG∽ΔDFE .
- D
ΔHGI∽ΔDEF .
Đáp án : A
ΔHIG và ΔDEF có ˆH=ˆD , ˆI=ˆE (gt) nên ΔHIG∽ΔDEF (g – g ).
Câu 40 : Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
- A
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
- B
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
- C
có hai cặp cạnh tương ứng bằng nhau.
- D
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Đáp án : B
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Câu 41 : Nếu ΔABC và ΔMNP có ˆA=ˆN ; ˆB=ˆM thì
- A
ΔABC∽ΔMNP .
- B
ΔCAB∽ΔNMP .
- C
ΔABC∽ΔPMN .
- D
ΔABC∽ΔNMP .
Đáp án : D
ΔABC và ΔNMP có ˆA=ˆN , ˆB=ˆM nên ΔABC∽ΔNMP (g – g ).