30 câu Trắc nghiệm Ứng dụng của định lí Thalès trong tam giác (có đáp án 2024) – Toán 8 Cánh diều

Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 2: Ứng dụng của định lí Thales trong tam giác đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 2.

1 107 lượt xem

Bài trước

Bài sau

Trắc nghiệm Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác

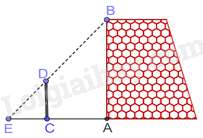
Câu 1 : Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao $A B$ của một bức tường như sau: Dùng một cái cọc $C D$ đặt cố định vuông góc với mặt đất, với $C D = 3$ m và $C A = 5$ m. Sau đó, các bạn đã phối hợp để tìm được điểm $E$ trên mặt đất là giao điểm của hai tia $B D, A C$ và đo được $C E = 2, 5$ m (Hình vẽ bên). Tính chiều cao $A B$ của bức tường.

A
3m
B
5m
C
6m
D
9m

Đáp án : D

Lời giải :

Xét $Δ E A B$ có $C D / / A B$ (do $C D$ và $A B$ cùng vuông góc với $C A$ )

Theo hệ quả định lí Thalès ta có: $\frac{C D}{A B} = \frac{E C}{E A}$ (*)

Mà $C A = 5$ m, $E C = 2, 5$ m $\Rightarrow C A = 2 E C \Rightarrow \frac{E C}{E A} = \frac{1}{3}$ và $C D = 3$ m

Thay vào (*) ta được $\frac{3}{A B} = \frac{1}{3} \Rightarrow A B = 9$ (m).

Vậy bức tường cao 9m.

Câu 2 : Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5m so với mặt đất, chân cọc cách gốc cây 8m và cách bóng của đỉnh cọc 2m. Tính chiều cao của cây. (Kết quả làm tròn đến chữ số thập phân thứ nhất).

A
10m
B
8m
C
7,5m
D
9m

Đáp án : C

Lời giải :

Xét $Δ A B E$ có $C D / / A B$ (cùng vuông góc với mặt đất)

$\Rightarrow \frac{C D}{A B} = \frac{E C}{E A}$ (hệ quả của định lí Thalès)

$\Leftrightarrow \frac{1, 5}{A B} = \frac{2}{2 + 8}$

$\Rightarrow A B = \frac{1, 5 (2 + 8)}{2} = 7, 5$ (m)

Vậy chiều cao của cây là 7,5m.

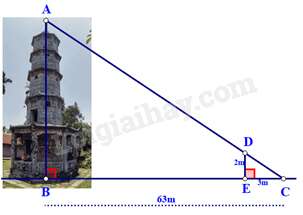
Câu 3 : Bóng của một tháp trên mặt đất có độ dài $B C = 63$ m. Cùng thời điểm đó, một cây cột $D E$ cao 2 mét cắm vuông góc với mặt đất có bóng dài 3 mét. Tính chiều cao của tháp?

A
63m
B
126m
C
21m
D
42m

Đáp án : D

Lời giải :

Ta có: $D E / / A B$ (cùng vuông góc $B C$ )

$\Rightarrow \frac{D E}{A B} = \frac{C E}{C B}$ (hệ quả định lí Thalès)

$\Leftrightarrow \frac{2}{A B} = \frac{3}{63}$

$\Rightarrow A B = \frac{2.63}{3} = 42$ m

Vậy chiều cao của tháp là 42m.

Câu 4 : Một cột đèn cao 10m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét).

A
4,8mg
B
6,8m
C
7m
D
10m

Đáp án : C

Lời giải :

$M C = M A + A C = 4, 8 + 2 = 6, 8$ (m)

Xét $Δ D C M$ có $A B / / C D$ nên $\frac{A B}{C D} = \frac{M A}{M C}$ (hệ quả định lí Thalès)

$\Leftrightarrow \frac{A B}{10} = \frac{4, 8}{6, 8} \Rightarrow A B = \frac{4, 8.10}{6, 8} \approx 7$ (m)

Vậy chiều cao của cây xanh đó là 7m.

Câu 5 : Giữa hai điểm $B$ và $C$ có một cái ao. Để đo khoảng cách $B C$ người ta đo được các đoạn thẳng $A D = 2$ , $B D = 10$ m và $D E = 5$ m. Biết $D E / / B C$ , tính khoảng cách giữa hai điểm $B$ và $C$ .

A
12m
B
30m
C
25m
D
13m

Đáp án : B

Lời giải :

Xét $Δ A B C$ có $D E / / B C$

$\Rightarrow \frac{A D}{A B} = \frac{D E}{B C}$

$\Leftrightarrow \frac{2}{10 + 2} = \frac{5}{B C}$

$\Rightarrow B C = \frac{5 (10 + 2)}{2} = 30$ m

Vậy khoảng cách giữa hai điểm $B$ và $C$ là 30m.

Câu 6 : Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết $B B^{'} = 20$ m, $B C = 30$ m và $B^{'} C = 40$ m. Tính độ rộng $x$ của khúc sông.

A
30m
B
60m
C
90m
D
120m

Đáp án : B

Lời giải :

Dùng hệ quả của định lý Thalès, ta có:

$\frac{A B}{A B^{'}} = \frac{B C}{B^{'} C^{'}} \Rightarrow \frac{x}{x + 20} = \frac{30}{40} \Rightarrow x = 60$ m.

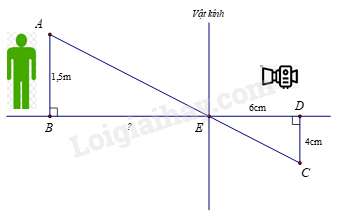
Câu 7 : Người ta dùng máy ảnh để chụp một người có chiều cao $A B = 1, 5$ m (như hình vẽ). Sau khi rửa phim thấy ảnh $C D$ cao 4cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là $E D = 6$ cm. Hỏi người đó đứng cách vật kính máy ảnh một đoạn $B E$ bao nhiêu cm?

A
150cm
B
200cm
C
225cm
D
250cm

Đáp án : C

Lời giải :

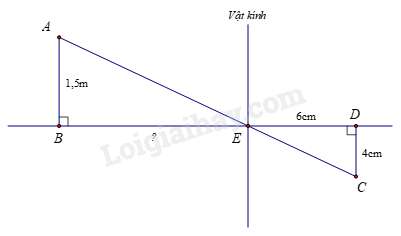
Đổi đơn vị: 1,5m=150cm.

Ta có: $A B / / C D$ (cùng vuông góc với $B D$ ) $\Rightarrow \frac{E B}{E D} = \frac{A B}{C D}$ (hệ quả định lí Thalès)

$\Rightarrow E B = \frac{E D . A B}{C D} = \frac{6.150}{4} = 225$ (cm)

Vậy người đứng cách vật kính máy ảnh là 225cm.

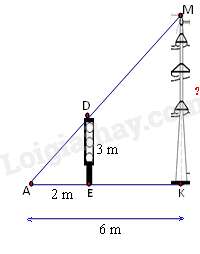
Câu 8 : Bóng $(A K)$ của một cột điện $(M K)$ trên mặt đất dài 6m. Cùng lúc đó một cột đèn giao thông $(D E)$ cao 3m có bóng $(A E)$ dài 2m. Tính chiều cao của cột điện $(M K)$ .

A
6cm
B
9cm
C
12cm
D
18cm

Đáp án : B

Lời giải :

Ta có : DE // MK

$\Rightarrow \frac{D E}{M K} = \frac{A E}{A K}$

$\Leftrightarrow \frac{3}{M K} = \frac{2}{6}$

$\Rightarrow M K = \frac{6.3}{2} = 9$ (m)

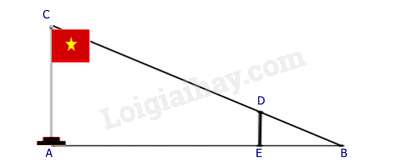
Câu 9 : Để đo chiều cao $A C$ của một cột cờ, người ta cắm một cái cọc $E D$ có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại $B$ , biết khoảng cách $B E$ là 1,5m và khoảng cách $A B$ là 9m.

Tính chiều cao $A C$ của cột cờ.

A
6m
B
9m
C
12m
D
18m

Đáp án : C

Lời giải :

Xét $Δ A B C$ có $A C / / E D (A C ⊥ A B, E D ⊥ A B)$

$\Rightarrow \frac{E B}{A B} = \frac{E D}{A C}$ (hệ quả của định lí Thalès)

$\Leftrightarrow \frac{1, 5}{9} = \frac{2}{A C}$

$\Rightarrow A C = 12$ (m)

Vậy chiều cao $A C$ của cột cờ là 12m.

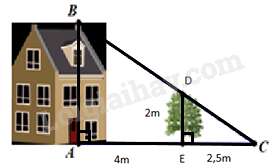
Câu 10 : Tính chiều cao $A B$ của ngôi nhà biết cái cây có chiều cao $E D = 2$ m và khoảng cách $A E = 4$ m, $E C = 2, 5$ m.

A
2,5m
B
5,2m
C
6,5m
D
4m

Đáp án : B

Lời giải:

Ta có: $E D / / A B$

$\Rightarrow \frac{A B}{E D} = \frac{A C}{E C}$ (hệ quả định lí Thalès)

$\begin{array}{l} \Leftrightarrow \frac{A B}{2} = \frac{4 + 2, 5}{2, 5} \\ \Leftrightarrow \frac{A B}{2} = \frac{6, 5}{2, 5} \end{array}$

$\Rightarrow A B = \frac{6, 5 .2}{2, 5} = 5, 2$ (m)

Vậy ngôi nhà cao 5,2m.

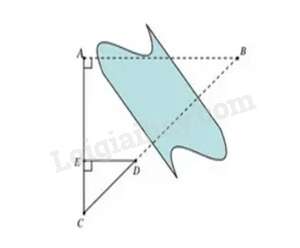
Câu 11 : Để đo khoảng cách giữa hai điểm $A$ và $B$ (không thể đo trực tiếp), người ta xác định các điểm $C, D, E$ như hình vẽ. Sau đó đo được khoảng cách giữa $A$ và $C$ là $A C = 6$ m, khoảng cách giữa $C$ và $E$ là $E C = 2$ m; khoảng cách giữa $E$ và $D$ là $D E = 3$ m. Tính khoảng cách giữa hai điểm $A$ và $B$ .

A
6m
B
9m
C
12m
D
18m

Đáp án : B

Lời giải:

Ta có: $A B / / E D$

$\Rightarrow \frac{E D}{A B} = \frac{C E}{A C}$ (hệ quả định lí Thalès)

$\Leftrightarrow \frac{3}{A B} = \frac{2}{6}$

$\Rightarrow A B = \frac{6.3}{2} = 9$ m

Vậy khoảng cách giữa hai điểm $A$ và $B$ là 9m.

Câu 12 : Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

A
80cm
B
40cm
C
160cm
D
120cm

Đáp án : A

Lời giải :

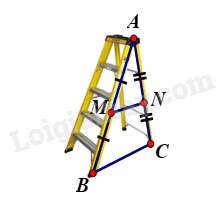
Gọi $M N$ là thanh ngang; $B C$ là độ rộng giữa hai bên thang.

$M N$ nằm chính giữa thang nên $M, N$ là trung điểm $A B$ và $A C$ .

$\Rightarrow \frac{A M}{A B} = \frac{A N}{A C} = \frac{1}{2}$

$\Rightarrow M N / / B C$ (định lí Thalès đảo)

$\Rightarrow \frac{A M}{A B} = \frac{A N}{A C} = \frac{M N}{B C}$ (hệ quả định lí Thalès)

$\Rightarrow M N = \frac{1}{2} B C = \frac{1}{2} \cdot 80 = 40$ (cm)

Vậy người thợ đã làm thanh ngang đó dài 80cm.

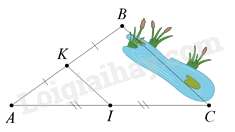
Câu 13 : Giữa hai điểm $B$ và $C$ bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài $B C$ mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng $K I$ dài 25m và $K$ là trung điểm của $A B$ , $I$ là trung điểm của $A C$ .

A
12,5m
B
50m
C
25m
D
100m

Đáp án : B

Lời giải :

Xét $Δ A B C$ có: $K$ là trung điểm của $A B$ , $I$ là trung điểm của $A C$

$\Rightarrow \frac{A K}{A B} = \frac{A I}{A C} = \frac{1}{2}$

$\Rightarrow K I / / B C$ (định lí Thalès đảo)

$\Rightarrow \frac{A K}{A B} = \frac{A I}{A C} = \frac{K I}{B C}$ (hệ quả định lí Thalès)

$\Rightarrow B C = 2 K I = 2.25 = 50$ (m)

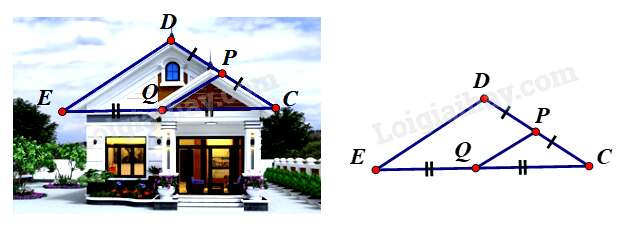
Câu 14 : Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái $P Q = 1, 5$ m. Chú thợ nhẩm tính chiều dài mái $D E$ biết $Q$ là trung điểm $E C$ , $P$ là trung điểm của $D C$ . Em hãy tính giúp chú thợ xem chiều dài mái $D E$ bằng bao nhiêu (xem hình vẽ minh họa)?

A
3m
B
6m
C
9m
D
12m

Đáp án : A

Lời giải :

Vì $Q$ là trung điểm $E C$ , $P$ là trung điểm của $D C$ nên

$\frac{C Q}{C E} = \frac{C P}{C D} = \frac{1}{2}$

$\Rightarrow Q P / / E D$ (định lí Thalès đảo)

$\Rightarrow \frac{C Q}{C E} = \frac{C P}{C D} = \frac{Q P}{E D}$ (hệ quả định lí Thalès)

$\Rightarrow D E = 2 P Q = 2.1, 5 = 3$ (m)

Vậy chiều dài mái $D E$ bằng 3m.

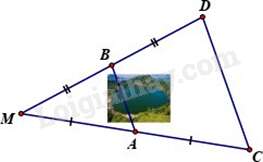
Câu 15 : Giữa 2 điểm $A$ và $B$ là một hồ nước. Biết $A, B$ lần lượt là trung điểm của $M C$ và $M D$ (như hình vẽ). Bạn Mai đi từ $C$ đến $D$ hết 120 bước chân, trung bình mỗi bước chân của Mai đi được 4dm. Hỏi khoảng cách từ $A$ đến $B$ là bao nhiêu mét?

A
12m
B
48m
C
6m
D
24m

Đáp án : D

Lời giải :

$A, B$ lần lượt là trung điểm của $M C$ và $M D$ .

$\Rightarrow \frac{M A}{M C} = \frac{M B}{M D} = \frac{1}{2}$

$\Rightarrow B A / / C D$ (định lí Thalès đảo)

$\Rightarrow \frac{M A}{M C} = \frac{M B}{M D} = \frac{B A}{C D}$ (hệ quả định lí Thalès)

$\Rightarrow B A = \frac{1}{2} \cdot C D = \frac{1}{2} \cdot 4.120 = 240 d m = 24 m$

Câu 16 : Để đo khoảng cách giữa hai điểm $A$ và $B$ bị ngăn cách bởi một hồ nước người ta đóng các cọc tại các vị trí $A, B, M, N, O$ như hình bên và đo được $M N = 45$ m. Tính khoảng cách $A B$ biết $M, N$ lần lượt là điểm chính giữa $O A$ và $O B$ .

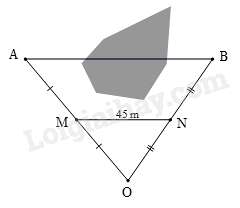
A
22,5m
B
45m
C
90m
D
67,5m

Đáp án : C

Lời giải :

$M, N$ lần lượt là điểm chính giữa $O A$ và $O B$ .

$\Rightarrow \frac{O M}{O A} = \frac{1}{2}; \frac{O N}{O B} = \frac{1}{2} \Rightarrow \frac{O M}{O A} = \frac{O N}{O B} \Rightarrow M N / / A B$ (định lí Thalès đảo)

$\Rightarrow \frac{O M}{O A} = \frac{O N}{O B} = \frac{M N}{A B}$ (hệ quả định lí Thalès)

$\Rightarrow A B = 2 M N = 2.45 = 90$ m.

Câu 17 : Để đo khoảng cách giữa hai điểm $A$ và $B$ bị ngăn cách bởi một hồ nước người ta đóng các cọc ở vị trí $A, B, C, D, E$ như hình vẽ. Người ta đo được $D E = 350$ m. Tính khoảng cách giữa hai điểm $A$ và $B$ .

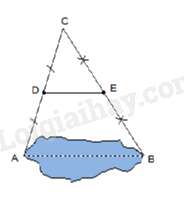
A
175m
B
350m
C
700m
D
525m

Đáp án : C

Lời giải :

Ta có: $C D = D A = \frac{A C}{2}; C E = E B = \frac{B C}{2}$
$\Rightarrow \frac{C D}{C A} = \frac{C E}{C B} = \frac{1}{2}$

$\Rightarrow D E / / A B$ (định lí Thalès đảo)

$\Rightarrow \frac{C D}{C A} = \frac{C E}{C B} = \frac{D E}{A B}$ (hệ quả định lí Thalès)

$\Rightarrow A B = 2 D E = 2.350 = 700$ m.

Câu 18 : Giữa 2 điểm $A$ và $N$ là một một hồ nước sâu. Để tính khoảng cách giữa 2 điểm $A$ và $N$ , một học sinh đã lấy $M$ làm mốc và lấy $H, G$ lần lượt là trung điểm của $M A, M N$ . Hỏi $A$ và $N$ cách nhau bao nhiêu mét. Biết khoảng cách giữa 2 điểm $H$ và $G$ là 62m.

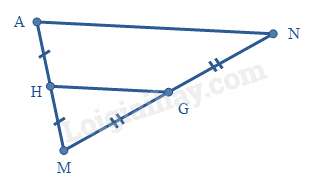
A
62m
B
31m
C
93m
D
124m

Đáp án : D

Lời giải :

$H, G$ lần lượt là trung điểm của $M A, M N$ .

$\Rightarrow \frac{M H}{M A} = \frac{1}{2}; \frac{M G}{M N} = \frac{1}{2} \Rightarrow \frac{M H}{M A} = \frac{M G}{M N} \Rightarrow H G / / A N$ (định lí Thalès đảo)ư

$\Rightarrow \frac{M H}{M A} = \frac{M G}{M N} = \frac{H G}{A N}$ (hệ quả định lí Thalès)
$\Rightarrow A N = 2 H G = 2.62 = 124$ m.

Câu 19 : Nhà tâm lý học Abraham Maslow (1908 – 1970) được xem như một trong những người tiên phong trong trường phái Tâm lý học nhân văn. Năm 1943, ông đã phát triển Lý thuyết về Thang bậc nhu cầu của con người (như hình vẽ bên). Trong đó, $B K = 6$ cm. Hãy tính đoạn thẳng $C J; E H$ ?

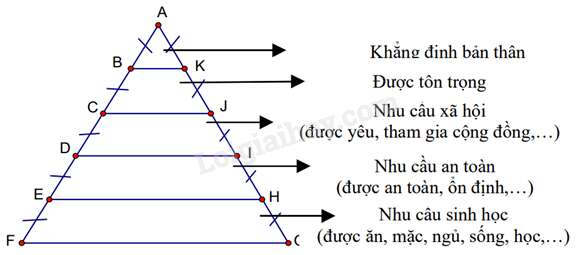
A
$C J = 6 c m; E H = 12 c m$
B
$C J = 12 c m; E H = 24 c m$
C
$C J = 9 c m; E H = 18 c m$
D
$C J = 12 c m; E H = 18 c m$

Đáp án : B

Lời giải :

Ta có: $A B = B C = C D = D E = E F = \frac{A F}{5}$ ;

$A K = K J = J I = I H = H O = \frac{A O}{5}$

$\begin{array}{l} A C = A B + B C = 2 A B \Rightarrow \frac{A B}{A C} = \frac{1}{2} \\ A J = A K + K J = 2 A K \Rightarrow \frac{A K}{A J} = \frac{1}{2} \end{array}} \Rightarrow \frac{A B}{A C} = \frac{A K}{A J}$

$\Rightarrow B K / / C J$ (định lí Thalès đảo)

$\Rightarrow \frac{A B}{A C} = \frac{A K}{A J} = \frac{B K}{C J}$ (hệ quả định lí Thalès)

$\Rightarrow C J = 2 B K = 2.6 = 12$ cm

$\begin{array}{l} A E = A B + B C + C D + D E = 4 A B \Rightarrow \frac{A C}{A E} = \frac{2 A B}{4 A B} = \frac{1}{2} \\ A H = A K + K J + J I + I H = 4 A K \Rightarrow \frac{A J}{A H} = \frac{2 A K}{4 A K} = \frac{1}{2} \end{array}} \Rightarrow \frac{A C}{A E} = \frac{A J}{A H}$

$\Rightarrow C J / / E H$ (định lí Thalès đảo)

$\Rightarrow \frac{A C}{A E} = \frac{A J}{A H} = \frac{C J}{E H}$ (hệ quả định lí Thalès)

$\Rightarrow E H = 2 C J = 2.12 = 24$ cm

Câu 20 : Để làm cây thông noel, người thợ sẽ dùng một cái khung sắt hình tam giác cân như hình vẽ bên, sau đó gắn mô hình cây thông lên. Cho biết thanh $B C = 120$ cm. Tính độ dài các thanh $G F, H E, I D$ .

A
$G F = 30 c m; H E = 60 c m; I D = 90 c m$
B
$G F = 30 c m; H E = 60 c m; I D = 120 c m$
C
$G F = 30 c m; H E = 90 c m; I D = 120 c m$
D
$G F = 60 c m; H E = 90 c m; I D = 120 c m$

Đáp án : A

Lời giải :

Ta có: $A G = G H = H I = I B = \frac{A B}{4}; A F = F E = E D = D C = \frac{A C}{4}$

Xét $Δ A B C$ có $\frac{A G}{A B} = \frac{A F}{A C} = \frac{1}{4}$

$\Rightarrow G F / / B C$ (định lí Thalès đảo)

$\Rightarrow \frac{A G}{A B} = \frac{A F}{A C} = \frac{G F}{B C}$ (hệ quả định lí Thalès)

$\Rightarrow G F = \frac{B C}{4} = \frac{120}{4} = 30$ (cm)

$\begin{array}{l} \frac{A G}{A H} = \frac{A G}{A G + G H} = \frac{A G}{2 A G} = \frac{1}{2} \\ \frac{A F}{A E} = \frac{A F}{A F + F E} = \frac{A F}{2 A F} = \frac{1}{2} \end{array}} \Rightarrow \frac{A G}{A H} = \frac{A F}{A E} = \frac{1}{2} \Rightarrow G F / / H E$ (định lí Thalès đảo)

$\Rightarrow \frac{A G}{A H} = \frac{A F}{A E} = \frac{G F}{H E}$ (hệ quả định lí Thalès)

$\Rightarrow H E = 2 G F = 2.30 = 60$ (cm)

$\begin{array}{l} \frac{A G}{A I} = \frac{A G}{A G + G H + H I} = \frac{A G}{3 A G} = \frac{1}{3} \\ \frac{A F}{A D} = \frac{A F}{A F + F E + E D} = \frac{A F}{3 A F} = \frac{1}{3} \end{array}} \Rightarrow \frac{A G}{A I} = \frac{A F}{A D} = \frac{1}{3}$

$\Rightarrow G F / / I D$ (định lí Thalès đảo)

$\Rightarrow \frac{A G}{A I} = \frac{A F}{A D} = \frac{G F}{I D}$ (hệ quả định lí Thalès)

$\Rightarrow I D = 3 G F = 3.30 = 90$ (cm)

1 107 lượt xem

Bài trước

Bài sau

30 câu Trắc nghiệm Ứng dụng của định lí Thalès trong tam giác (có đáp án 2024) – Toán 8 Cánh diều

Giới thiệu

Liên kết

Chính sách

Kết nối

30 câu Trắc nghiệm Ứng dụng của định lí Thalès trong tam giác (có đáp án 2024) – Toán 8 Cánh diều

CHỌN BỘ SÁCH BẠN MUỐN XEM