Lý thuyết Đường trung trực của một đoạn thẳng (Cánh diều 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 9: Đường trung trực của một đoạn thẳng

A. Lý thuyết

1. Định nghĩa

– Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.

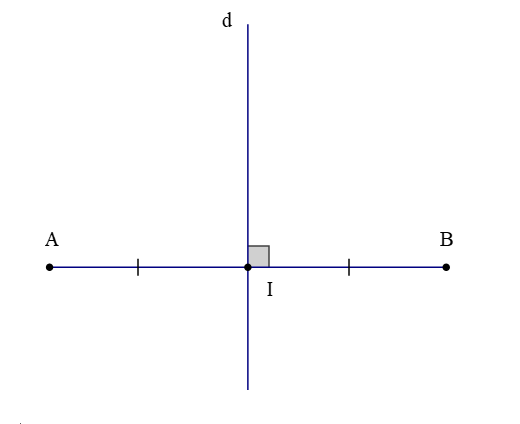
Quan sát hình vẽ trên, ta có:

+ Đoạn thẳng AB; trung điểm I của đoạn thẳng AB;

+ Đường thẳng d ⊥ AB tại I.

Do đó, đường thẳng d là đường trung trực của đoạn thẳng AB.

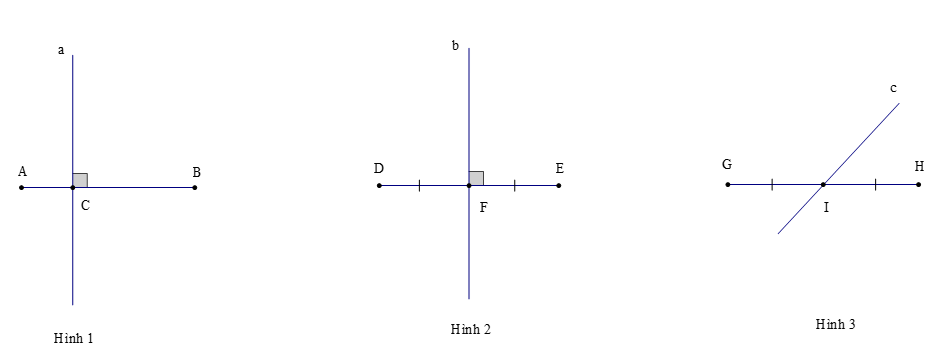
Ví dụ: Trong các hình dưới đây, hãy chỉ ra các đường trung trực trong mỗi hình (nếu có):

Hướng dẫn giải

– Quan sát hình 1, ta thấy:

Đường thẳng a ⊥ AB tại C nhưng đường thẳng a không đi qua trung điểm của  đoạn thẳng AB.

Do đó, đường thẳng a không là đường trung trực của đoạn thẳng AB.

– Quan sát hình 2, ta thấy:

Đường thẳng b ⊥ DE tại F và đường thẳng b đi qua trung điểm F của đoạn thẳng DE.

Do đó, đường thẳng b là đường trung trực của đoạn thẳng DE.

– Quan sát hình 3, ta thấy:

Đường thẳng c đi qua trung điểm I của đoạn thẳng GH nhưng đường thẳng c không vuông góc với đoạn thẳng GH.

Do đó, đường thẳng c không là đường trung trực của đoạn thẳng GH.

2. Tính chất

– Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

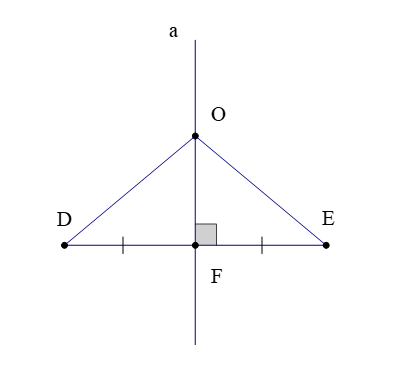
Quan sát hình trên, ta có:

Đường thẳng a là đường trung trực của đoạn thẳng DE;

Điểm O nằm trên đường thẳng a.

Khi đó ta có OD = OE.

Ví dụ: Qua trung điểm O của AB kẻ đường trung trực d. Trên d lấy hai điểm E và F sao cho O nằm giữa E và F. Chứng minh rằng $\widehat{\text{EAF}}=\widehat{\text{EBF}}$.

Hướng dẫn giải

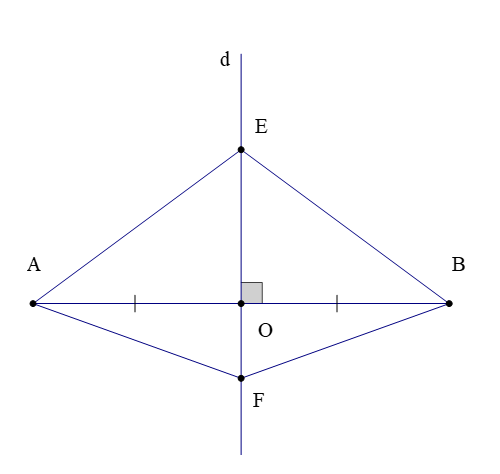
Vì E và F nằm trên đường trung trực d của đoạn thẳng AB (giả thiết)

Nên EA = EB và FA = FB (tính chất đường trung trực)

Xét ∆EAF và ∆EBF ta có:

EA = EB (chứng minh trên),

FA = FB (chứng minh trên),

EF là cạnh chung.

Suy ra ∆EAF = ∆EBF (c.c.c)

Do đó $\widehat{\text{EAF}}=\widehat{\text{EBF}}$(hai góc tương ứng).

Vậy $\widehat{\text{EAF}}=\widehat{\text{EBF}}$.

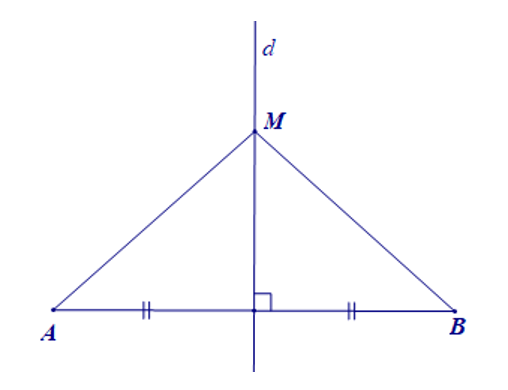
– Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Gọi d là đường trung trực của đoạn thẳng AB, M là điểm sao cho MA = MB (như hình vẽ bên dưới). Ta có M nằm trên đường trung trực d của đoạn thẳng AB.

Ví dụ: Cho ∆ABC cân tại A có $\widehat{\text{BAC}}=80°$, đường trung trực của AB cắt BC tại D. Tính $\widehat{\text{ADB}}.$

Hướng dẫn giải

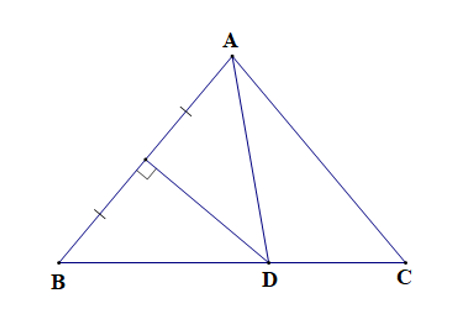
∆ABC cân tại A nên $\widehat{\text{B}}=\widehat{\text{C}}$ (tính chất tam giác cân).

Xét ∆ABC có $\widehat{\text{BAC}}+\widehat{\text{B}}+\widehat{\text{C}}=180°$(tổng ba góc trong một tam giác)

Hay $80°+\widehat{\text{B}}+\widehat{\text{B}}=180°$(vì $\widehat{\text{B}}=\widehat{\text{C}}$)

Suy ra 2$\widehat{\text{B}}=180°-80°=100°$

Suy ra $\widehat{\text{B}}=100°:2=50°.$

Theo bài ta có D nằm trên đường trung trực của AB nên DA = DB.

Suy ra ∆DAB cân tại D.

Do đó $\widehat{\text{B}}=\widehat{\text{BAD}}=50°$ (tính chất tam giác cân)

Xét ∆DAB có: $\widehat{\text{B}}+\widehat{\text{BAD}}+\widehat{\text{ADB}}=180°$(tổng ba góc trong một tam giác)

Hay $\widehat{\text{ADB}}=180°-\widehat{\text{B}}-\widehat{\text{ABD}}=180°-50°-50°=80°$

Vậy $\widehat{\text{ADB}}=80°$.

3. Vẽ đường trung trực của một đoạn thẳng

Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ đường trung trực của đoạn thẳng AB, biết AB = a cm.

Để vẽ đường trung trực của đoạn thẳng AB, ta làm theo các bước:

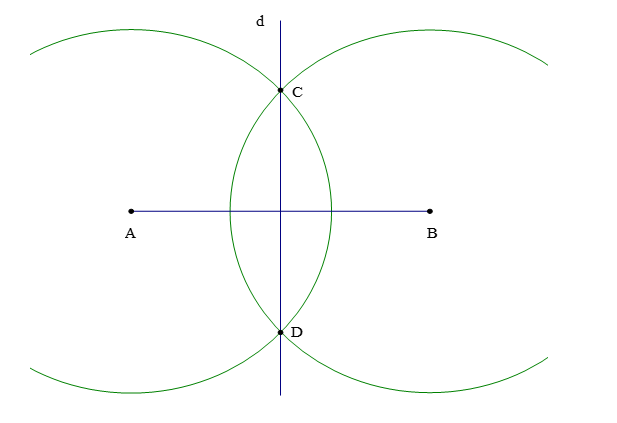
Bước 1: Vẽ đoạn thẳng AB = a cm.

Bước 2: Vẽ một phần đường tròn tâm A bán kính R (biết R > $\frac{\mathrm{a}}{2}$).

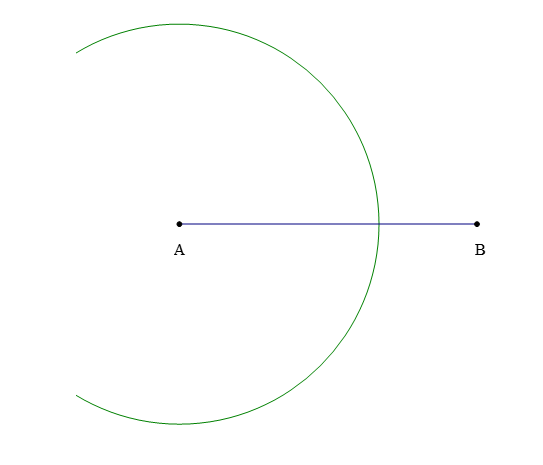
 Bước 3: Vẽ một phần đường tròn tâm B bán kính R (biết R > $\frac{\mathrm{a}}{2}$), cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm C và D.

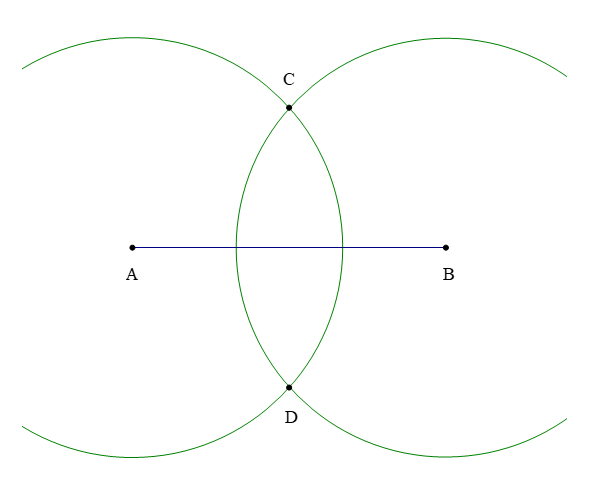
Bước 4: Vẽ đường thẳng đi qua hai điểm C và D. Đường thẳng CD là đường trung trực của đoạn thẳng AB.

B. Bài tập tự luyện

B.1 Bài tập trắc nghiệm

Câu 1. Cho ∆ABC cố định, đường phân giác AI (I ∈ BC). Trên đoạn thẳng IC lấy điểm H. Từ H kẻ đường thẳng song song với AI, cắt AB kéo dài tại E và cắt AC tại F. Chọn khẳng định đúng.

A. Đường trung trực của đoạn thẳng EF không đi qua đỉnh A của ∆ABC;           

B. Đường trung trực của đoạn thẳng EF luôn đi qua đỉnh A của ∆ABC;

C. ∆AEF cân tại E;         

D. ∆AEF cân tại F.

Hướng dẫn giải

Đáp án đúng là: B

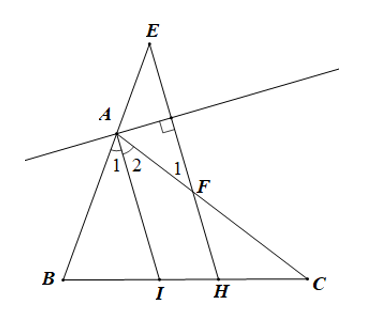
Vì HE // AI (giả thiết).

Nên $\widehat{\mathrm{AEF}}=\widehat{{\mathrm{A}}_1}$ (hai góc đồng vị) và $\widehat{{\mathrm{F}}_1}=\widehat{{\mathrm{A}}_2}$ (hai góc so le trong).

Mà $\widehat{{\mathrm{A}}_1}=\widehat{{\mathrm{A}}_2}$ (do AI là phân giác của $\widehat{\mathrm{BAC}}$).

Suy ra $\widehat{\mathrm{AEF}}=\widehat{{\mathrm{F}}_1}$.

Do đó ∆AEF cân tại A.

Suy ra đáp án C, D sai.

Vì ∆AEF cân tại A nên AE = AF.

Suy ra A thuộc đường trung trực của đoạn thẳng EF.

Do đó đường trung trực của đoạn thẳng EF luôn đi qua đỉnh A của ∆ABC.

Vậy ta chọn đáp án B.

Câu 2. Cho đoạn thẳng AB. Dựng các tam giác PAB cân tại P và tam giác QAB cân tại Q như hình bên.

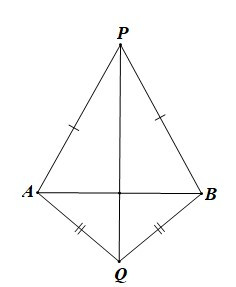
Chọn khẳng định đúng nhất.

A. PQ đi qua trung điểm của đoạn thẳng AB;                   

B. PQ vuông góc với AB;                   

C. PQ không vuông góc với AB;                   

D. PQ là đường trung trực của đoạn thẳng AB.

Hướng dẫn giải

Đáp án đúng là: D

Ta có ∆PAB cân tại P nên PA = PB.

Suy ra P thuộc đường trung trực của đoạn thẳng AB  (1).

Tương tự, ta có ∆QAB cân tại Q nên QA = QB.

Suy ra Q thuộc đường trung trực của đoạn thẳng AB  (2).

Từ (1), (2), ta suy ra PQ là đường trung trực của đoạn thẳng AB.

Vì đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.

Nên đáp án D đúng nhất.

Vậy ta chọn đáp án D.

Câu 3. Cho ∆MNP vuông tại M có $\widehat{\mathrm{P}}=30°$. Trên tia đối của tia MP, lấy điểm Q sao cho MQ = MP. Tính số đo $\widehat{\mathrm{QNP}}$.

A. 30°;                  

B. 120°;                

C. 60°;                  

D. 180°.

Hướng dẫn giải

Đáp án đúng là: B

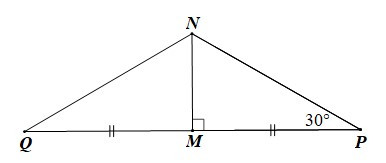
Ta có MQ = MP (giả thiết).

Suy ra M là trung điểm PQ                  (1)

Lại có ∆MNP vuông tại M.

Suy ra NM ⊥ MP hay NM ⊥ PQ          (2)

Từ (1), (2), ta suy ra NM là đường trung trực của đoạn thẳng PQ.

Do đó NQ = NP (tính chất đường trung trực của đoạn thẳng)

Suy ra ∆PQN cân tại N.

Khi đó $\widehat{\mathrm{NQP}}=\widehat{\mathrm{NPQ}}=30°$ (tính chất tam giác cân)

∆PQN có: $\widehat{\mathrm{QNP}}+\widehat{\mathrm{NQP}}+\widehat{\mathrm{NPQ}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{QNP}}=180°-\widehat{\mathrm{NQP}}-\widehat{\mathrm{NPQ}}=180°-30°-30°=120°$.

Do đó $\widehat{\mathrm{QNP}}=120°$.

Vậy ta chọn đáp án B.

B.2 Bài tập tự luận

Bài 1. Cho $\widehat{\text{xOy}}=30°$. Trên tia Ox lấy điểm E, trên tia Oy lấy điểm F. Lấy điểm D sao cho OF là đường trung trực của ED.

a) Chứng minh $\widehat{\mathrm{OFE}}=\widehat{\mathrm{OFD}};$

b) Chứng minh: ∆OED đều.

Hướng dẫn giải

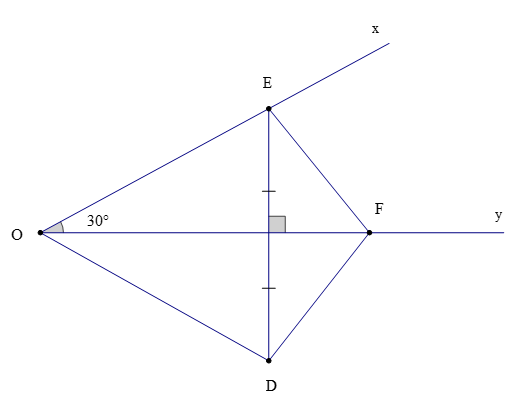
Vì OF là đường trung trực của ED (giả thiết)

Nên OE = OD và FE = FD (tính chất đường trung trực của đoạn thẳng)

Xét ∆OEF và ∆ODF có:

OE = OD (chứng minh trên),

FE = FD (chứng minh trên),

OF là cạnh chung.

Do đó ∆OEF = ∆ODF (c.c.c)

Suy ra $\widehat{\mathrm{OFE}}=\widehat{\mathrm{OFD}}$ (hai góc tương ứng).

Vậy $\widehat{\mathrm{OFE}}=\widehat{\mathrm{OFD}}$.

b) Theo phần a ta có: ∆OEF = ∆ODF nên $\widehat{\mathrm{EOF}}=\widehat{\text{DOF}}=30°$(hai góc tương ứng)

Ta lại có $\widehat{\text{EOD}}=\widehat{\mathrm{EOF}}+\widehat{\text{FOD}}=30°+30°=60°$

Xét ∆OED có OE = OD nên ∆OED cân tại O.

Mà ∆OED cân tại O có $\widehat{\text{EOD}}=60°$(chứng minh trên)

Do đó ∆OED đều.

Vậy ∆OED là tam giác đều.

Bài 2. Cho ∆ABC có AB = 8cm; BC = 6cm. Qua trung điểm M của AC, kẻ đường vuông góc với AC cắt AB tại K. Tính chu vi ∆KBC.

Hướng dẫn giải

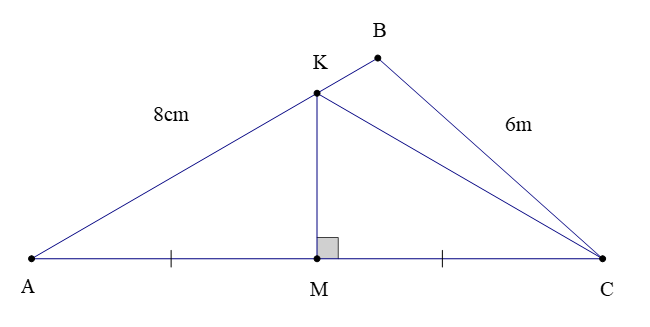
Theo bài ta có M là trung điểm của AC và KM ⊥ AC tại M nên KM là đường trung trực của AC

Suy ra KA = KC (tính chất đường trung trực của đoạn thẳng) (1)

Ta có AB = AK + KB (2)

Từ (1) và (2) suy ra AB = KC + KB

Mà AB = 8 cm nên KC + KB = 8 cm.

Ta có chu vi ∆KBC là:

P = KB + KC + BC = 8 + 6 = 14 (cm).

Vậy chu vi ∆KBC bằng 14 cm.

Bài 3. Cho tam giác ABC cân tại A. Các đường phân giác BE, CF cắt nhau tại H. Chứng minh:

a) AH là trung trực của EF;

b) AH là trung trực của BC.

Hướng dẫn giải

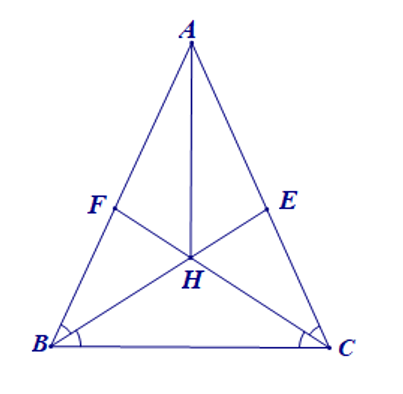
a) Vì BE là phân giác của $\widehat{\text{ABC}}$ nên $\widehat{\text{ABE}}=\widehat{\text{CBE}}=\frac{1}{2}\widehat{\text{ABC}}$  (1)

CF là phân giác của $\widehat{\text{ACB}}$ nên $\widehat{\text{ACF}}=\widehat{\text{FCB}}=\frac{1}{2}\widehat{\text{ACB}}$  (2)

Mà $\widehat{\text{ABC}}=\widehat{\text{ACB}}$ (vì ∆ABC cân tại A)  (3)

Từ (1), (2) và (3) suy ra $\widehat{\text{ABE}}=\widehat{\text{ACF}}$

• Xét ∆ABE và ∆ACF có:

AB = AC (vì ∆ABC cân tại A),

$\widehat{\text{ABE}}=\widehat{\text{ACF}}$ (chứng minh trên),

AH là cạnh chung.

Do đó ∆ABE = ∆ACF (c.g.c)

Suy ra AE = AF (hai cạnh tương ứng)

Suy ra A nằm trên đường trung trực của EF        (4)

• Vì AB = AC và AF = AE (chứng minh trên)

Nên AB – AF = AC – AE

Hay BF = CE.

• Vì ∆ABE = ∆ACF (chứng minh trên)

Nên $\widehat{\mathrm{AEB}}=\widehat{\mathrm{AFC}}$ (hai góc tương ứng)

Mà $\widehat{\mathrm{AEB}}+\widehat{\mathrm{CEB}}=180°$ (hai góc kề bù)

$\widehat{\mathrm{AFC}}+\widehat{\mathrm{BFC}}=180°$(hai góc kề bù)

Do đó $\widehat{\mathrm{CEB}}=\widehat{\mathrm{BFC}}$ hay $\widehat{\mathrm{CEH}}=\widehat{\mathrm{BFH}}$

• Xét ∆BFH và ∆CEH có:

 $\widehat{\mathrm{BFH}}=\widehat{\mathrm{CEH}}$ (chứng minh trên),

BF = CE (chứng minh trên),

$\widehat{\mathrm{FBH}}=\widehat{\mathrm{ECH}}$ (do $\widehat{\text{ABE}}=\widehat{\text{ACF}}$).

Do đó ∆BFH = ∆CEH (g.c.g)

Suy ra HF = HE (hai cạnh tương ứng)

Suy ra H nằm trên đường trung trực của EF          (5)

Từ (4) và (5) suy ra A, H nằm trên đường trung trực của EF

Suy ra AH là đường trung trực của EF

Vậy AH đường trung trực của EF.

b) Vì ∆BFH = ∆CEH (chứng minh câu a)

Suy ra BH = CH (hai cạnh tương ứng)

Do đó H nằm trên trung trực của BC

Mặt khác: AB = AC (chứng minh câu a)

Nên A nằm trên trung trực của BC

Do đó AH là đường trung trực của BC.

Vậy AH là đường trung trực của BC.