Lý thuyết Số hữu tỉ (Cánh diều 2024) Toán 7

Lý thuyết Toán lớp 7 Chương 1: Số hữu tỉ

A. Lý thuyết

1. Số hữu tỉ

- Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}\left(a,b\in \mathbb{Z},b\ne 0\right)$.

- Tập hợp các số hữu tỉ kí hiệu là ℚ.

Chú ý:

- Mỗi số nguyên là một số hữu tỉ.

- Các phân số bằng nhau là cách viết khác nhau của cùng một số hữu tỉ.

2. Biểu diễn số hữu tỉ trên trục số

- Tương tự số nguyên ta có thể biểu diễn mọi số hữu tỉ trên trục số.

- Điểm biểu diễn số hữu tỉ a được gọi là điểm a.

- Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số ta chọn một trong những phân số đó để biểu diễn. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.

- Nếu số hữu tỉ chưa viết dưới dạng phân số thì ta viết lại chúng dưới dạng phân số rồi biểu diễn phân số đó trên trục số.

3. Số đối của một số hữu tỉ

- Trên trục số hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc O và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số hữu tỉ a, kí hiệu là –a.

- Số đối của số 0 là 0.

4. So sánh các số hữu tỉ

4.1 So sánh hai số hữu tỉ

Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.

- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a.

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.

- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương

- Nếu a < b và  b < c thì a < c.

4.2 Cách so sánh hai số hữu tỉ

+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.

+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.

4.3 Minh họa trên trục số

Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :

- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.

- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.

5. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế

5.1 Quy tắc cộng, trừ hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.

5.2 Tính chất của phép cộng các số hữu tỉ

- Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.

- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.

5.3 Quy tắc chuyển vế

Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:

x + y = z ⇒ x = z – y

x – y = z ⇒ x = z + y

6. Nhân, chia hai số hữu tỉ

6.1 Quy tắc nhân, chia hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

- Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.

6.2 Tính chất của phép nhân các số hữu tỉ

Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.

Nhận xét:

- Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là $\frac{1}{a}$. Ta có $a\cdot \frac{1}{a}=1$

- Số nghịch đảo của số hữu tỉ $\frac{1}{a}$ là a.

- Nếu a, b là hai số hữu tỉ và b ≠ 0 thì $a:b=a\cdot \frac{1}{b}$.

7. Phép tính lũy thừa với số mũ tự nhiên

- Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x: $x^n=\underset{n\text{ thua\hspace{0.17em}so x}}{\underbrace{x.x.\mathrm{...}\text{ .x}}}$ với $n\in {\mathbb{N}}^{*}$

Số x được gọi là cơ số, n gọi là số mũ.

- Quy ước x1 = x.

Chú ý:

 xn đọc là “x mũ n” hoặc “x lũy thừa n” hoặc “lũy thừa bậc n của x”.

x2 còn được gọi là “x bình phương” hay “bình phương của x”.

x3 còn gọi là “x lập phương” hay “lập phương của x”.

Chú ý: Để viết lũy thừa bậc n của phân số $\frac{a}{b}$, ta phải viết $\frac{a}{b}$ trong dấu ngoặc ( ), tức là ${\left(\frac{a}{b}\right)}^n$.

8. Tích và thương của hai lũy thừa cùng cơ số

- Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:  

xm . xn = xm+n $\left(m,n\in \mathbb{N}\right)$.

- Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia :

xm : xn = xm – n  $(x\ne 0;\text{ m}\ge \text{n; m,n}\in \mathbb{N})$

- Quy ước x0 = 1 (x ≠ 0).

9. Lũy thừa của một lũy thừa

Khi tính lũy thừa của một lũy thừa ta giữ nguyên cơ số và nhân hai số mũ:

${\left(x^m\right)}^n=x^{m.n}\text{ (m,n}\in \mathbb{N})$.

10. Thứ tự thực hiện các phép tính

- Đối với biểu thức không có dấu ngoặc:

+ Khi biểu thức chỉ có các phép tính cộng và trừ (hoặc chỉ có phép tính nhân và chia), ta thực hiện phép tính theo thứ tự từ bên trái sang phải.

+ Khi biểu thức có các phép tính cộng, trừ, nhân, chia, ta thực hiện phép tính nhân và chia trước, rồi đến cộng và trừ.

+ Khi biểu thức có chứa các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

- Đối với biểu thức có chứa dấu ngoặc:

+ Khi biểu thức có chứa dấu ngoặc, ta thực hiện các phép tính trong ngoặc trước.

+ Khi các biểu thức có chứa các dấu ngoặc ( ), [ ]; { } thì thứ tự thực hiện phép tính như sau: ( ) → [ ] →{ }.

11. Quy tắc dấu ngoặc

- Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữa nguyên dấu của các số hạng bên trong dấu ngoặc.

a + (b + c) = a + b + c

a + (b – c) = a + b – c

-  Khi bỏ dấu ngoặc có dấu “–” đằng trước, ta phải đổi dấu của các số hạng bên trong dấu ngoặc: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu  “+”.

a – (b + c) = a – b – c

a – (b – c) = a – b + c

Nhận xét: Nếu đưa các số hạng vào trong dấu ngoặc có dấu “–” đằng trước thì phải đổi dấu các số hạng đó.

12. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn

- Các số thập phân chỉ gồm hữu hạn chữ số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân mà trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi mãi được gọi là số thập phân vô hạn tuần hoàn. Chữ số hoặc cụm chữ số lặp đi lặp lại mãi mãi đó được gọi là chu kì của số thập phân vô hạn tuần hoàn.

13. Biểu diễn thập phân của số hữu tỉ

- Mỗi số hữu tỉ đều viết được dưới dạng phân số $\frac{a}{b}\text{ (a,b}\in \mathbb{Z};\text{ b\hspace{0.17em}> 0)}$. Thực hiện phép tính

a : b ta có thể biểu diễn số hữu tỉ đó dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

- Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

B. Bài tập tự luyện

B.1 Bài tập trắc nghiệm

Câu 1. Số nghịch đảo của số − 0,8 là:

A. - 0,8;

B. $\frac{-\text{ 8}}{10};$

C. $\frac{5}{4};$

D. $\frac{-\text{ 5}}{4}.$

Hướng dẫn giải

Đáp án đúng là: D.

Do số nghịch đảo của số hữu tỉ a khác 0 là $\frac{1}{\text{a}}$ nên số nghịch đảo của − 0,8 là: $\frac{1}{-\text{ 0,8}}\text{ = }\frac{-\text{ 10}}{8}\text{ = }\frac{-\text{ 5}}{4}.$ 

Câu 2. Kết luận nào đúng về giá trị của biểu thức $\text{A = }\frac{1}{5}-\left[\left(\frac{-\text{ 2}}{3}\right)-\left(\frac{1}{3}\text{ + }\frac{5}{6}\right)\right]?$

A. A < 2

B. A > 2

C. A < 1

D. A < 0

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $A\text{ = }\frac{1}{5}-\left[\left(\frac{-\text{ 2}}{3}\right)-\left(\frac{1}{3}\text{ + }\frac{5}{6}\right)\right]$

$=\frac{1}{5}-\left[\left(\frac{-\text{ 2}}{3}\right)-\left(\frac{2}{6}\text{ + }\frac{5}{6}\right)\right]$

$=\frac{1}{5}-\left(\frac{-\text{ 2}}{3}-\frac{7}{6}\right)$

$=\frac{1}{5}-\left(\frac{-\text{ 4}}{6}-\frac{7}{6}\right)$

$=\frac{1}{5}-\frac{-\text{ 11}}{6}$

$=\frac{6}{30}-\frac{-\text{ 55}}{30}$

$=\frac{6-\left(-\text{ 55}\right)}{30}$

$=\frac{61}{30}.$

Do $A=\frac{61}{30}>\frac{60}{30}=2$ nên A > 2.

Câu 3. Giá trị của x1 bằng bao nhiêu?

A. 1;

B. 0;

C. x;

D. 2.

Hướng dẫn giải

Đáp án đúng là: C.

Ta có: xn là tích của n thừa số x nên quy ước x1 = x.

Câu 5. Biết m là một số thập phân vô hạn tuần hoàn và 2,347923 < m < 2,4452347. Tìm m?

A. m = 2,(3);

B. m = 2,(34);

C. m = 2,(4);

D. m = 2,(445).

Hướng dẫn giải

Đáp án đúng là: C.

Ta có: 2,(3) = 2,333… < 2,347923 do đó m = 2,(3) là sai.

2,(34) = 2,343434… < 2,347923 do đó m = 2,(34) là sai.

2,347923 < 2,444… < 2,4452347 do đó m = 2,(4) là đúng.

2,(445) = 2,445445445… > 2,4452347 do đó m = 2,(445) là sai.

Vậy m = 2,(4).

Câu 4. Hình nào biểu diễn đúng điểm A của số hữu tỉ $\frac{1}{4}$ trên trục số?

A.                 

B. 

C. 

D. Không có hình nào đúng.

Hướng dẫn giải

Đáp án đúng là: B

Để xác định điểm biểu diễn $\frac{1}{4}$ ta chia đoạn từ điểm 0 đến điểm 1 thành 4 phần bằng nhau. Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 phần sẽ được điểm A.

Do đó trục số của phương án B là đúng.

B.2 Bài tập tự luận

Bài 1. Tìm số đối của số hữu tỉ $\frac{2}{-7}$.

Hướng dẫn giải

Số đối của số hữu tỉ $\frac{2}{-7}$ là: $-\left(\frac{2}{-7}\right)=-\left(-\frac{2}{7}\right)=\frac{2}{7}$.

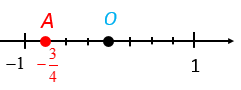
Bài 2. Hãy biểu diễn số hữu tỉ $-\frac{3}{4}$ trên trục số.

Hướng dẫn giải

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành bốn phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ).

- Đi theo chiều ngược chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm A. Điểm A chính là điểm biểu diễn số hữu tỉ $-\frac{3}{4}$.

Bài 3. Tính

a) $\frac{-1}{4}+\frac{-1}{3}$;

b) $\frac{-2}{5}-\frac{3}{11}$;

c) $\frac{-5}{9}:\frac{-7}{18}$;

d) $\frac{-4}{9}\cdot 0,75$.

Hướng dẫn giải

a) $\frac{-1}{4}+\frac{-1}{3}=\frac{-3}{12}+\frac{-4}{12}=\frac{-7}{12}$.

b) $\frac{-2}{5}-\frac{3}{11}=\frac{-22}{55}-\frac{15}{55}=\frac{-37}{55}$.

c) $\frac{-5}{9}:\frac{-7}{18}=\frac{-5}{9}\cdot \frac{18}{-7}=\frac{-10}{-7}=\frac{10}{7}$.

d) Ta viết $0,75=\frac{75}{100}=\frac{3}{4}$. Khi đó: $\frac{-4}{9}\cdot 0,75=\frac{-4}{9}\cdot \frac{3}{4}=\frac{-1}{3}$.

Bài 4. So sánh hai số hữu tỉ $\frac{2}{-7}$ và $\frac{-3}{11}$.

Hướng dẫn giải

Hai số hữu tỉ trên đã viết dưới dạng phân số vì vậy để so sánh ta đưa phân số về có cùng mẫu dương, sau đó ta chỉ cần so sánh hai tử số.

Ta có $\frac{2}{-7}=\frac{-2}{7}=\frac{-22}{77}$ và  $\frac{-3}{11}=\frac{-21}{77}$

Vì $-22<-21$ nên $\frac{-22}{77}<\frac{-21}{77}$. Suy ra $\frac{2}{-7}$< $\frac{-3}{11}$.

Bài 5. Thực hiện các phép tính:

a) $\frac{2}{3}+\frac{3}{4}\cdot \left(\frac{-4}{9}\right)$;

b) $\left(\frac{3}{4}-0,2\right)\cdot \left(0,4-\frac{4}{5}\right)$.

Hướng dẫn giải

a) $\frac{2}{3}+\frac{3}{4}\cdot \left(\frac{-4}{9}\right)=\frac{2}{3}+\frac{-1}{3}=\frac{1}{3}$.

b)

$$\begin{gathered} \left(\frac{3}{4}-0,2\right)\cdot \left(0,4-\frac{4}{5}\right) \\ =\left(\frac{3}{4}-\frac{1}{5}\right).\left(\frac{2}{5}-\frac{4}{5}\right) \\ =\left(\frac{15}{20}-\frac{4}{20}\right)\cdot \frac{-2}{5} \\ =\frac{11}{20}\cdot \frac{-2}{5}=\frac{-11}{50} \end{gathered}$$

Bài 6. Tìm x, biết

a) $x+\frac{-1}{3}=\frac{4}{15}$ ;

b) $x\cdot \frac{3}{2}=2,4$.

Hướng dẫn giải

 a) $x+\frac{-1}{3}=\frac{4}{15}$  

$\text{x =}\frac{4}{15}-\frac{-1}{3}$

$\text{x = }\frac{4}{15}-\frac{-5}{15}$

$x=\frac{9}{15}$

$\text{x = }\frac{3}{5}$      

Vậy $\text{x = }\frac{3}{5}$.

b) $x\cdot \frac{3}{2}=2,4$

$x=2,4:\frac{3}{2}$

$x=2,4:1,5$

$x=1,6$

Vậy x = 1,6.

Bài 7. Viết mỗi tích sau dưới dạng lũy thừa

a) $\left(-\frac{3}{2}\right)\cdot \left(\frac{-3}{2}\right)\cdot \left(\frac{-3}{2}\right)$ ;

b) (–1,2) .( –1,2) . (–1,2). (–1,2). (–1,2).

Hướng dẫn giải

a) Ta thấy có ba thừa số $\frac{-3}{2}$ nên ta có $\left(-\frac{3}{2}\right)\cdot \left(\frac{-3}{2}\right)\cdot \left(\frac{-3}{2}\right)={\left(\frac{-3}{2}\right)}^3$

b) Ta thấy có năm thừa số (–1,2) nên ta có (–1,2) .( –1,2) . (–1,2). (–1,2). (–1,2) = (–1,2)5

Bài 8. So sánh

a) ${\left(\frac{2}{3}\right)}^3\cdot \left(\frac{2}{3}\right)$ và ${\left(\frac{2}{3}\right)}^4$ ;

b) ${\left(0,1\right)}^{10}:{\left(0,1\right)}^4$ và ${\left[{\left(0,1\right)}^2\right]}^3$.

Hướng dẫn giải

a) Ta có : ${\left(\frac{2}{3}\right)}^3\cdot \left(\frac{2}{3}\right)={\left(\frac{2}{3}\right)}^3\cdot {\left(\frac{2}{3}\right)}^1={\left(\frac{2}{3}\right)}^{3+1}={\left(\frac{2}{3}\right)}^4$.

Vậy ${\left(\frac{2}{3}\right)}^3\cdot \left(\frac{2}{3}\right)$ = ${\left(\frac{2}{3}\right)}^4$

b) Ta có:  ${\left(0,1\right)}^{10}:{\left(0,1\right)}^4={\left(0,1\right)}^{10-4}={\left(0,1\right)}^6$ 

và  ${\left[{\left(0,1\right)}^2\right]}^3={\left(0,1\right)}^{2.3}={\left(0,1\right)}^6$

Vậy ${\left(0,1\right)}^{10}:{\left(0,1\right)}^4$ = ${\left[{\left(0,1\right)}^2\right]}^3$.

Bài 9. Viết mỗi số thập phân hữu hạn sau dưới dạng phân số tối giản: 2,5;  –0,16.

Hướng dẫn giải

Ta viết các số thập phân hữu hạn thành phân số thập phân sau đó rút gọn đến phân số tối giản.

Ta có $2,5=\frac{25}{10}=\frac{5}{2}$.

Ta có $-0,16=-\frac{16}{100}=-\frac{4}{25}$.

Bài 10. Viết mỗi phân số sau dưới dạng số thập phân hữu hạn: $\frac{11}{40};\frac{-14}{25}$.

Hướng dẫn giải

Ta thực hiện phép chia 11 : 40 = 0,275. Vậy $\frac{11}{40}=0,275$.

Ta thực hiện phép chia –14 : 25 = –0,56. Vậy $\frac{-14}{25}=-0,56$.