Lý thuyết Góc ở vị trí đặc biệt (Cánh diều 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 1: Góc ở vị trí đặc biệt

A. Lý thuyết Góc ở vị trí đặc biệt

1. Hai góc kề nhau

Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.

Ví dụ:

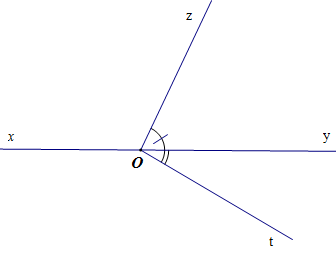
Hai góc yOz và yOt trong hình vẽ có chung đỉnh O, có một cạnh chung là Oy, hai cạnh còn lại là Oz và Ot nằm về hai phía của đường thẳng xy.

Vì vậy hai góc yOz và yOt là hai góc kề nhau.

Tính chất:

- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó. Khi đó hai góc xOy và yOz là hai góc kề nhau và $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox, Oz), ta cũng có: $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

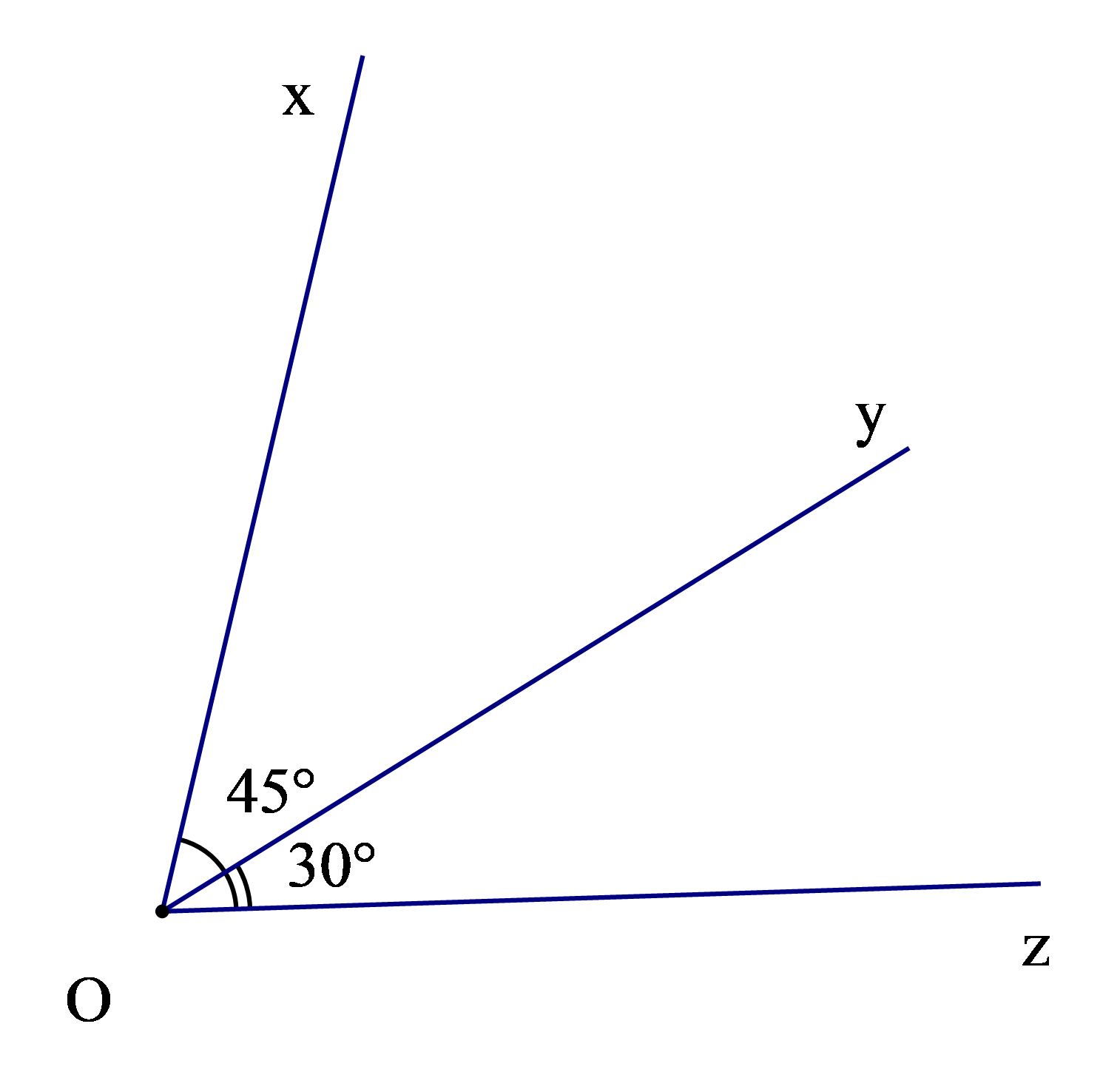
Ví dụ: Trong hình hai góc xOy và yOz có phải là hai góc kề nhau không? Tính số đo góc xOz ?

Hướng dẫn giải

Tia Oy nằm trong góc xOz nên góc xOy và góc yOz là hai góc kề nhau.

Và $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}=45°+30°=75°$.

Vậy hai góc xOy và yOz là hai góc kề nhau và $\widehat{xOz}=75°$.

2. Hai góc bù nhau. Hai góc kề bù

- Hai góc bù nhau là hai góc có tổng bằng 180°.

- Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Chú ý: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau là hai góc kề bù.

Ví dụ:

a)

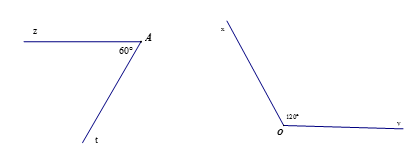
Ta có : $\widehat{zAt}+\widehat{xOy}=60°+120°=180°$.

Vì hai góc zAt và xOy có tổng bằng 180° nên góc zAt và xOy là hai góc bù nhau.

b)

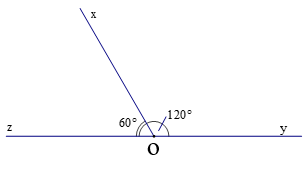
- Hai góc xOz và góc xOy có đỉnh O chung và cạnh Ox chung ; Hai cạnh Oy và Oz nằm về hai phía của đường thẳng chứa tia Ox. Vì thế, hai góc xOz và góc xOy kề nhau.

- Ta có : $\widehat{xOz}+\widehat{xOy}=60°+120°=180°$, vậy nên hai góc xOz và xOy là hai góc bù nhau.

Hai góc xOz và xOy là hai góc vừa kề nhau vừa bù nhau.

Vậy, góc xOz và góc xOy là hai góc kề bù.

3. Hai góc đối đỉnh

- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Hai góc đối đỉnh thì bằng nhau.

Ví dụ :

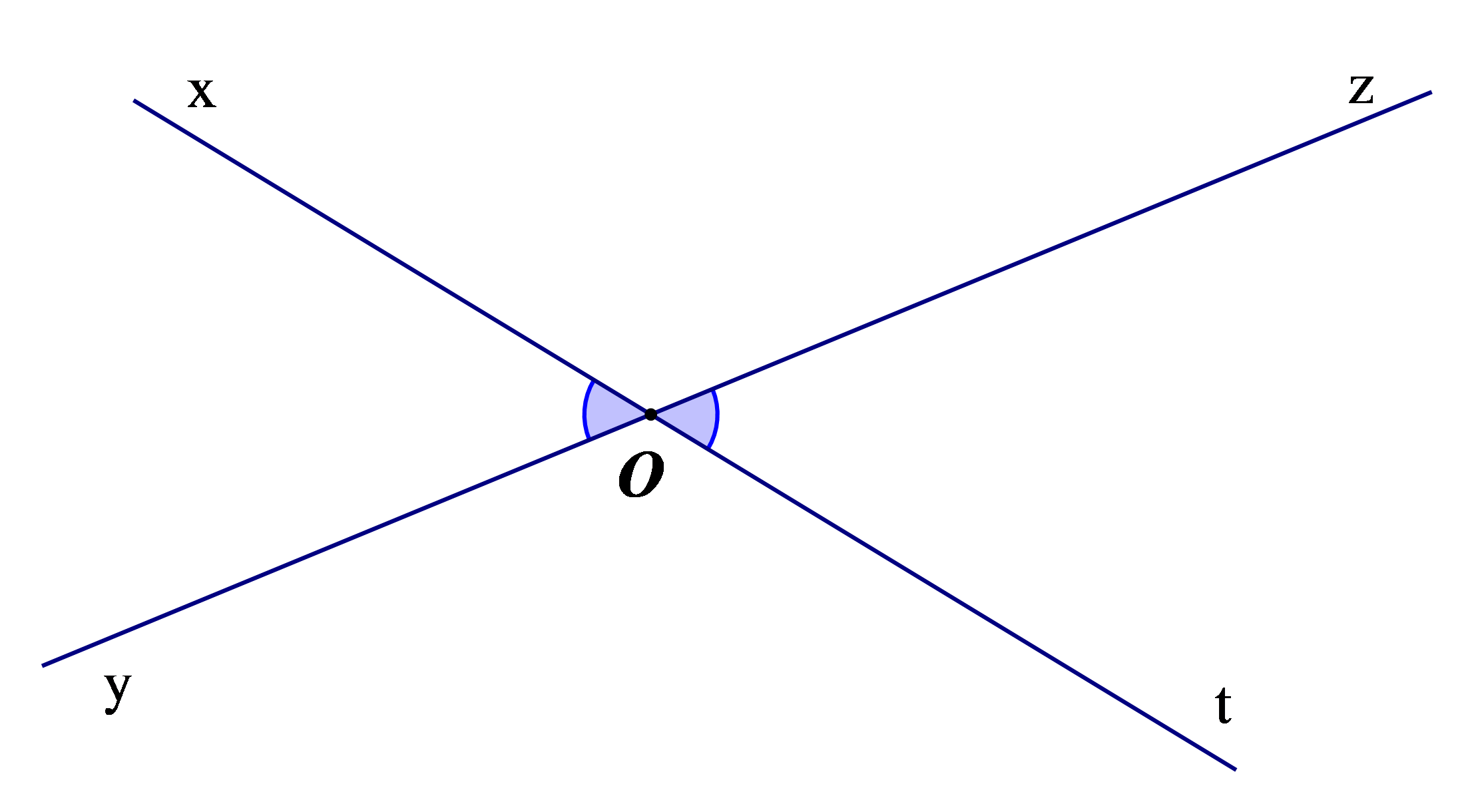
Cạnh Ot của góc tOz là tia đối của cạnh Ox của góc xOy;

Cạnh Oz của góc tOz là tia đối của cạnh Oy của góc xOy;

Vì vậy, góc xOy và góc tOz là hai góc đối đỉnh, nên $\widehat{xOy}=\widehat{tOz}$.

Tương tự, góc xOz và góc tOy cũng là hai góc đối đỉnh, nên $\widehat{xOz}=\widehat{tOy}$.

B. Bài tập tự luyện

B.1 Bài tập trắc nghiệm

Câu 1. Tìm số đo x và y trong hình vẽ dưới đây:

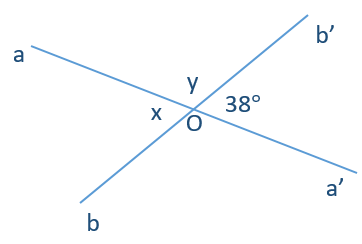
A. x = 38° và y = 52°;

B. x = 38° và y = 142°;                                                  

C. x = 142° và y = 38°;                                                  

D. x = 52° và y = 38°.

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

+ Góc aOb và góc b'Oa' là hai góc đối đỉnh nên $x=\widehat{aOb}=\widehat{b^{\text{'}}O{a}^{\text{'}}}=38°$.

+ Góc aOb' và góc b'Oa' là hai góc kề bù nên

$\widehat{aOb\text{'}}+\widehat{b^{\text{'}}O{a}^{\text{'}}}=180°\Rightarrow \widehat{aOb\text{'}}=180°-\widehat{b^{\text{'}}O{a}^{\text{'}}}=180°-38°=142°$.

Hay y = 142°

Vậy x = 38° và y = 142°.

Câu 2. Trong các hình dưới đây hình nào vẽ hai góc kề nhau là không đúng.

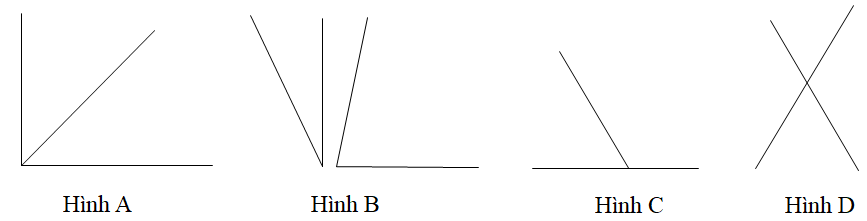
A. Hình A;                                                                     

B. Hình B;                                                                     

C. Hình C;                                                                     

D. Hình D.

Hướng dẫn giải

Đáp án đúng là: B

Hai góc kề nhau là có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.

Đáp án B không đúng vì hai góc không có đỉnh chung và cạnh chung.

Suy ra chọn đáp án B.

Câu 3. Hai góc đối đỉnh thì:

A. bằng nhau;                                                                

B. có tổng bằng 180°;                                                    

C. kề nhau;                                                                    

D. có hiệu bằng 180°.

Hướng dẫn giải

Đáp án đúng là: A

Hai góc đối đỉnh thì bằng nhau.

B.2 Bài tập tự luận

Bài 1. Biết góc xOz và xOt là hai góc kề bù. Hãy tính góc xOt.

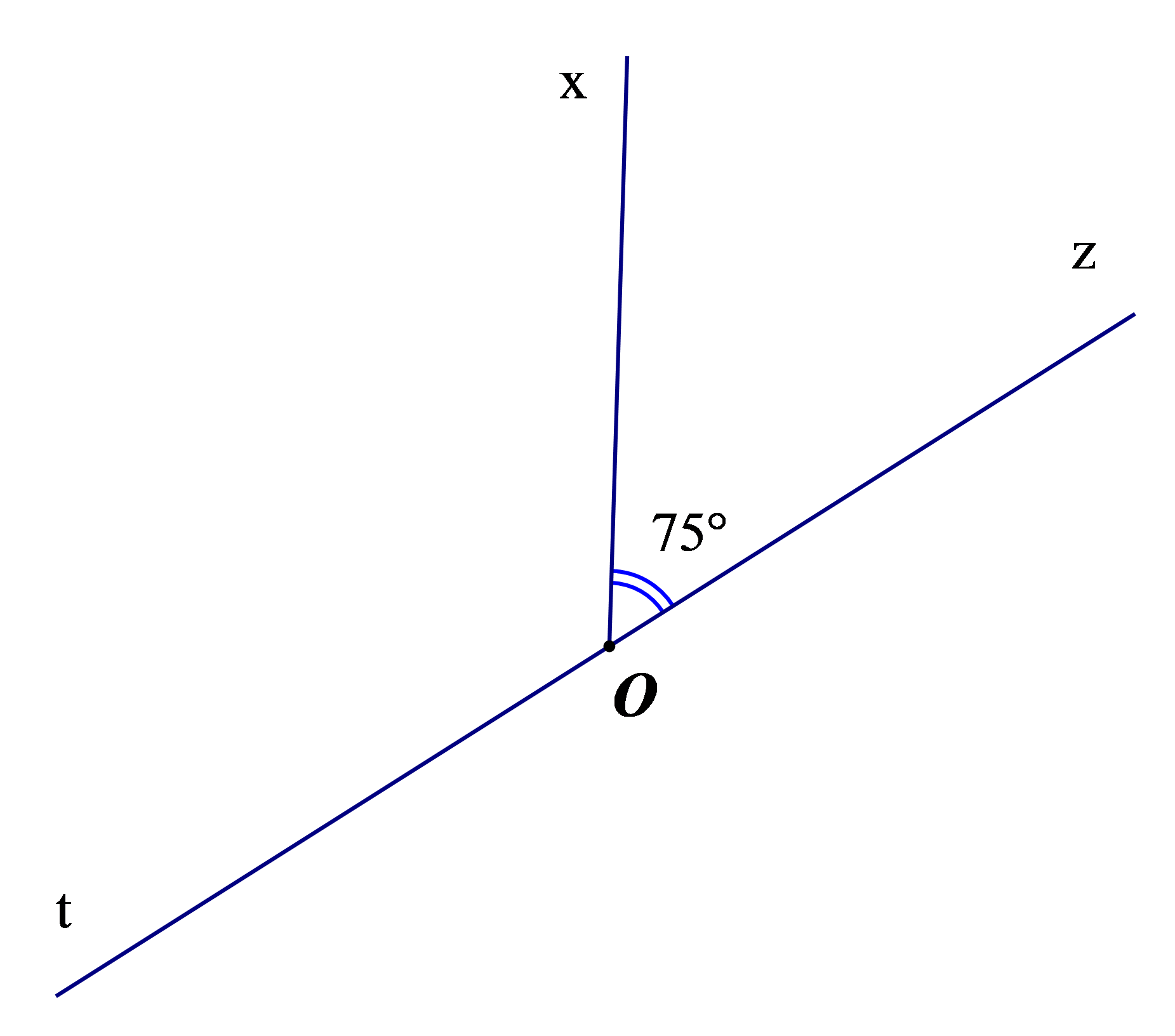
Hướng dẫn giải

Vì góc xOz và góc xOt là hai góc kề bù nên $\widehat{xOz}+\widehat{xOt}=180°$.

Suy ra $75°+\widehat{xOt}=180°$ suy ra $\widehat{xOt}=180°-75°=105°$.

Vậy $\widehat{xOt}=105°$.

Bài 2. Tìm x trong hình vẽ

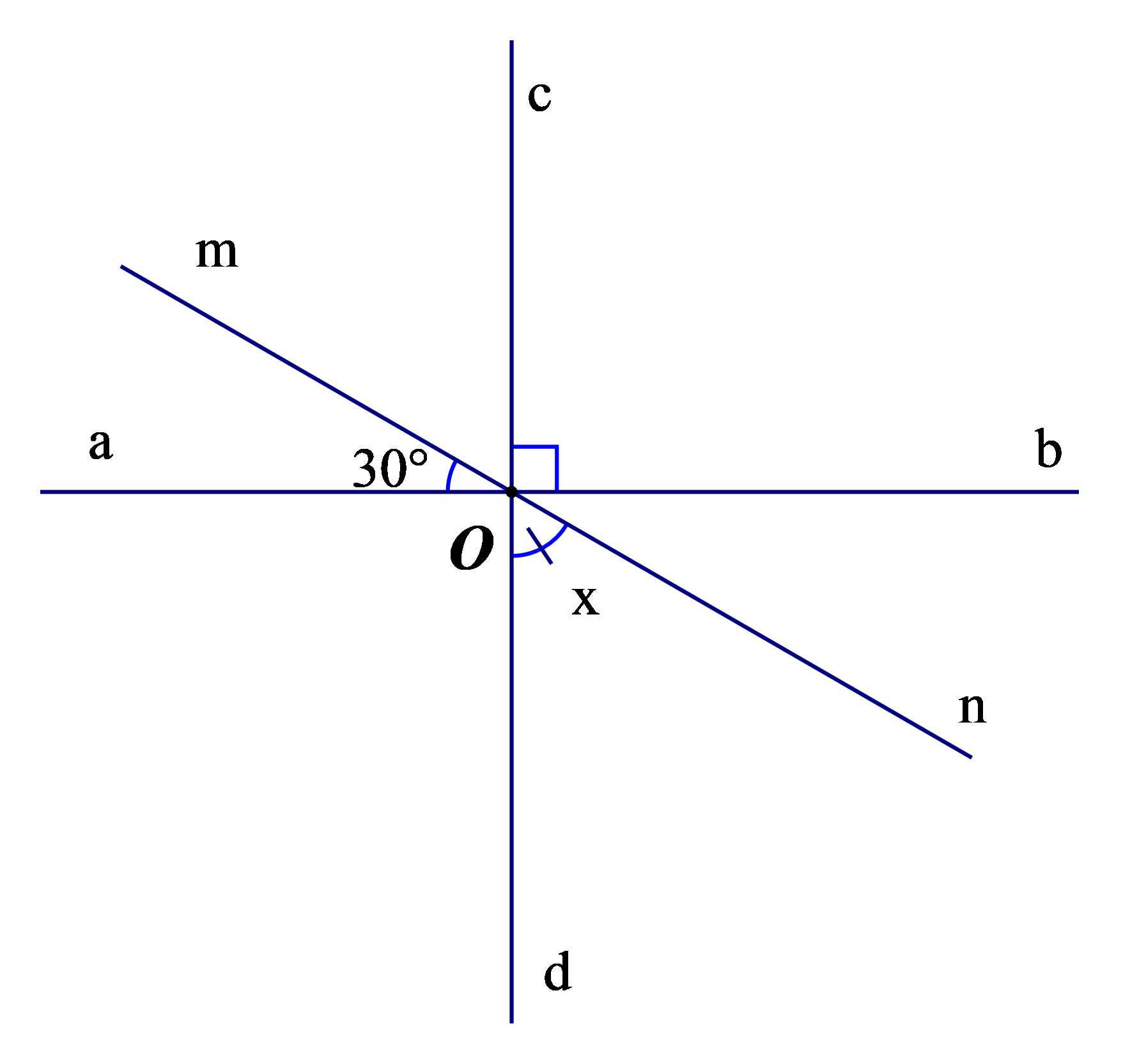
Hướng dẫn giải

Góc aOc và góc cOb kề bù, mà $\widehat{cOb}=90°$ (góc vuông).

Nên $\widehat{aOc}=180°-\widehat{cOb}=180°-90°=90°$.

Ta có góc aOm và góc mOc là hai góc kề nhau.

Nên $\widehat{aOc}=\widehat{aOm}+\widehat{mOc}$, mà $\widehat{aOc}=90°$ 

Suy ra: $\widehat{mOc}=\widehat{aOc}-\widehat{aOm}=90°-30°=60°$.

Vì góc mOc và góc nOd đối đỉnh nên ta có $x=\widehat{nOd}=\widehat{mOc}=60°$.

Vậy $x=60°$.