Lý thuyết Giá trị tuyệt đối của một số thực (Cánh diều 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 3: Giá trị tuyệt đối của một số thực

A. Lý thuyết Giá trị tuyệt đối của một số thực

1. Khái niệm

- Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu |x|.

Nhận xét:

- Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.

- Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.

Ví dụ:

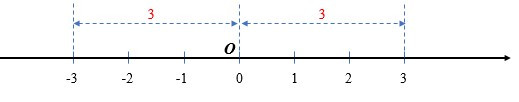
- Khoảng cách từ điểm 3 đến gốc 0 là 3 nên giá trị tuyệt đối của số 3 là 3, tức là |3| = 3.

- Khoảng cách từ điểm –3 đến gốc 0 là 3 nên giá trị tuyệt đối của số –3 là 3, tức là |–3| = 3.

- Số 3 và –3 là hai số đối nhau, |3| = |–3| = 3.

2. Tính chất

- Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| = x (x > 0).

- Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| = – x (x < 0).

- Giá trị tuyệt đối của 0 là 0: |0| = 0.

Nhận xét: Với mỗi số thực x, ta có:

+)    $\left|\mathrm{x}\right|=\left\{\begin{array}{c}\mathrm{x}\mathrm{khi}\text{ x }\ge \text{0}\\ -\mathrm{x}\text{ khi x < 0}\end{array}\right.$.

+)    |– x| = |x|.

Ví dụ: Tìm |– 76| ;   |3,1|

Vì – 76 < 0 nên |–76| = – (–76) = 76.

Vì 3,1 > 0 nên |3,1| = 3,1.

Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là AB = |a – b|.

Ví dụ: Tính độ dài đoạn thẳng AB trên hình vẽ sau:

a)

Ta có AB  =  OA + OB = |–3| + |1| =  3 + 1 = 4.

Hay AB = |–3 – 1| = |–4| = 4.

b)

Ta có AB = OA – OB = |–4| – |–1| = 4 – 1 = 3.

Hay AB = |(–4) – (– 1)| = |– 3| = 3.

B. Bài tập tự luyện

B.2 Bài tập trắc nghiệm

Câu 1. Cho biểu thức N = |3x – 0,5| + $\left|-1\frac{3}{4}\right|$. Khi x = –2 thì giá trị của N là:

A. $-\frac{33}{4};$ 

B. $\frac{27}{4};$ 

C. $\frac{33}{4};$ 

D. $\frac{59}{4};$ 

Hướng dẫn giải

Đáp án đúng là: C.

Thay x = –2 vào biểu thức N = |3x – 0,5| + $\left|-1\frac{3}{4}\right|$ ta được:

N = |3.(– 2) – 0,5| + $\left|-\frac{7}{4}\right|$ 

N = |–6 – 0,5| + $\left[-\left(-\frac{7}{4}\right)\right]$ 

$\mathrm{N}=\left|-6,5\right|+\frac{7}{4}$ 

$\mathrm{N}=6,5+\frac{7}{4}$ 

$\mathrm{N}=\frac{65}{10}+\frac{7}{4}$ 

$\mathrm{N}=\frac{130}{20}+\frac{35}{20}$ 

$\mathrm{N}=\frac{165}{20}$ 

$\mathrm{N}=\frac{33}{4}$

Câu 2. Chọn khẳng định đúng.

A. |–0,6| >  |–0,7|;

B. |–0,6| = –0,6;

C. $\left|\sqrt{0,7}\right|>\left|-\sqrt{0,7}\right|;$ 

D. $\left|\frac{2}{3}\right|>\left|-\frac{1}{3}\right|$ .

Hướng dẫn giải

Đáp án đúng là: D.

+) Ta có –0,6 <  0 nên |–0,6| = –(–0,6) = 0,6. Do đó phương án B sai.

Vì –0,7 <  0 nên |–0,7| = –(–0,7) = 0,7.

Vì 0,6 < 0,7 nên |–0,6| < |–0,7|. Do đó phương án A sai.

+) Vì $\sqrt{0,7}$ và $-\sqrt{0,7}$ là hai số đối nhau nên $\left|\sqrt{0,7}\right|=\left|-\sqrt{0,7}\right|$. Do đó phương án C sai.

+) Vì $\frac{2}{3}>0$ nên $\left|\frac{2}{3}\right|=\frac{2}{3}$;

Vì $-\frac{1}{3}<0$ nên $\left|-\frac{1}{3}\right|=-\left(-\frac{1}{3}\right)=\frac{1}{3}$ 

Vì $\frac{2}{3}>\frac{1}{3}$ nên $\left|\frac{2}{3}\right|>\left|-\frac{1}{3}\right|$. Do đó phương án D đúng.

Câu 3. Tìm tất cả các giá trị x thoả mãn $\left|\mathrm{x}\right|=\left|-\frac{1}{2}\right|$.

A. $\mathrm{x}=\frac{1}{2}$;

B. $\mathrm{x}=-\frac{1}{2};$

C. $\mathrm{x}=\frac{1}{2}$ hoặc $\mathrm{x}=-\frac{1}{2}$;

D. Không có giá trị nào của x thoả mãn.

Hướng dẫn giải

Đáp án đúng là: C.

$\left|\mathrm{x}\right|=\left|-\frac{1}{2}\right|$

$\left|\mathrm{x}\right|=-\left(-\frac{1}{2}\right)$ 

$\left|\mathrm{x}\right|=\frac{1}{2}$ 

Suy ra $\mathrm{x}=\frac{1}{2}$ hoặc $\mathrm{x}=-\frac{1}{2}$.

Vậy $\mathrm{x}=\frac{1}{2}$ hoặc $\mathrm{x}=-\frac{1}{2}$.

B.2 Bài tập tự luận

Bài 1. Tìm |– 34| ;   $\left|-\sqrt{27}\right|$ ;  $\left|\frac{-2}{-3}\right|$ .

Hướng dẫn giải

| – 34|  = – (–34) = 34

$\left|-\sqrt{27}\right|$ = $-\left(-\sqrt{27}\right)$ = $\sqrt{27}$

$\left|\frac{-2}{-3}\right|$ = $\left|\frac{2}{3}\right|$  = $\frac{2}{3}$

Bài 2. Tìm độ dài đoạn thẳng AB trong hình vẽ sau:

Hướng dẫn giải

Cách 1: Ta có AB = OA + OB = | –3| + |2| = 3 + 2 = 5.

Cách 2 (Dùng chú ý ở trên):  Ta có AB = | –3 – 2| = | –5| = 5.

Bài 3. Tính giá trị của biểu thức sau:

a) | – 100|  – | 34|;

b) |12|  + 3. | – 8|.

Hướng dẫn giải

a) |– 100|  – |34| = 100 – 34 = 66.

b) |12|  + 3. |– 8| = 12 + 3.8 = 12 + 24 = 36.

Bài 4. Tìm x biết

a) |x| = 1;

b) |x – 3| = – 2;

c) |x + 0,5| = 4.

Hướng dẫn giải

a) |x| = 1 nên x = 1 hoặc x =  –1

b) | x – 3| ≥ 0 với mọi số thực x, nên không có số thực x nào thỏa mãn | x – 3| = –2

c) | x + 0,5| = 4 nên x + 0,5 = 4 hoặc x + 0,5 = –4

Với  x + 0,5 = 4 thì x = 3,5

Với x + 0,5 = –4 thì x = –5,5