Lý thuyết Dấu hiệu chia hết cho 3, cho 9 (Chân trời sáng tạo 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 3, cho 9

Video giải Toán 6 Bài 8: Dấu hiệu chia hết cho 3, cho 9 - Chân trời sáng tạo

A. Lý thuyết Dấu hiệu chia hết cho 3, cho 9

1. Dấu hiệu chia hết cho 9

Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.

Ví dụ:

a) Số 1 944 chia hết cho 9 vì có tổng các chữ số là 1 + 9 + 4 + 4 = 18 chia hết cho 9.

b) Số 7 325 không chia hết cho 9 vì có tổng các chữ số là 7 + 3 + 2 + 5 = 17 không chia hết cho 9.

2. Dấu hiệu chia hết cho 3

Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.

Ví dụ:

a) Số 90 156 chia hết cho 3 vì có tổng các chữ số là 9 + 0 + 1 + 5 + 6 = 21 chia hết cho 3.

b) Số 6 116 không chia hết cho 3 vì có tổng các chữ số là 6 + 1 + 1 + 6 = 14 không chia hết cho 3.

B. Bài tập tự luyện

Bài 1. Tổng (hiệu) sau chia hết cho 3 hay 9?

a) 1251 + 5316;

b) 5436 – 1324;

c) 1 . 2 . 3 . 4 . 5 . 6 + 27.

Hướng dẫn giải

a) Tổng các chữ số của 1251 là 1 + 2 + 5 + 1 = 9 chia hết cho 3 và 9.

Tổng các chữ số của 5 316 là 5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.

Vậy 1251 + 5316 chia hết cho 3 nhưng không chia hết cho 9.

b) Tổng các chữ số của 5436 có 5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.

Tổng các chữ số của 1324 có 1 + 3 + 2 + 4 = 10 không chia hết cho 3 và 9.

Vậy 5436 – 1324 không chia hết cho 3 và 9.

c) Tích 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 (vì tích này có thừa số là 3).

Ta có: 1 . 2 . 3 . 4 . 5 . 6

= 1 . 2 . 3 . 4 . 5 . (3 . 2)

= 1 . 2 . 4 . 5 . (3 . 3) . 2

= 1 . 2 . 4 . 5 . 9 . 2 chia hết cho 9 (vì nó có thừa số là 9).

Do đó 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 và 9.

Tổng các chữ số của 27 là 2 + 7 = 9 chia hết cho 3 và 9.

Vậy 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 3 và 9.

Bài 2. Cho 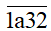 chia hết cho 9. Tìm số thay thế cho a.

Hướng dẫn giải

Tổng các chữ số của 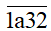 là 1 + a + 3 + 2 = a + 6 = a + 6.

Nên để 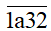 chia hết cho 9 thì a + 6 phải chia hết cho 9.

Do a là các số tự nhiên từ 0 đến 9 nên:

0 + 6 ≤ a + 6 ≤ 9 + 6.

Hay 6 ≤ a + 6 ≤ 15.

Số chia hết cho 9 từ 6 đến 15 chỉ có đúng một số là 9 nên a + 6 = 9

Do đó a = 3.

Vậy số thay thế cho a chỉ có thể là 3.

Bài 3: Cho 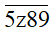 chia hết cho 3 và chia hết cho 9. Hãy tìm chữ số z.

Hướng dẫn giải

Vì một số bất kỳ nếu chia hết cho 9 thì cũng chia hết cho 3 nên ta chỉ xét 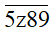 chia hết cho 9.

Để 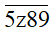 ⋮ 9 thì (5 + z + 8 + 9) ⋮ 9

Hay (22 + z) ⋮ 9 nên z = 5.

Vậy với z = 5 thì  chia hết cho 3 và chia hết cho 9.