Lý thuyết Hình học trực quan (Chân trời sáng tạo 2024) Toán 6

Lý thuyết Toán lớp 6 Chương 7: Hình học trực quan

Video giải Toán 6 Chương 7: Hình học trực quan – Chân trời sáng tạo

A. Lý thuyết Toán lớp 6 Chương 7: Hình học trực quan

1. Hình có trục đối xứng. Trục đối xứng

Có một đường thẳng d chia hình thành hai phần mà khi ta gấp hình theo đường thẳng d thì hai phần đó chồng khít lên nhau.

Những hình như thế là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.

2. Hình có tâm đối xứng. Tâm đối xứng

Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm Ota được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứngvà điểm O được gọi là tâm đối xứngcủa hình.

B. Bài tập tự luyện

Bài 1. Những chữ cái nào có trục đối xứng?

Lời giải:

- Chữ H có tâm đối xứng (như hình vẽ).

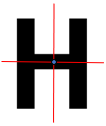
- Chữ O có tâm đối xứng (như hình vẽ).

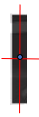
- Chữ I có tâm đối xứng (như hình vẽ).

- Chữ A không có tâm đối xứng.

- Chữ N có tâm đối xứng (như hình vẽ).

Vậy những chữ cái có tâm đối xứng là: H, O, I, N.

Bài 2. Tìm tâm đối xứng của mỗi hình sau đây.

Lời giải:

Tâm đối xứng của mỗi hình được biểu diễn như sau:

- Hình vuông:

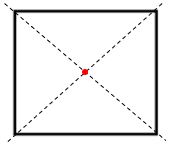
- Hình chữ nhật:

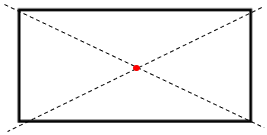
- Hình thoi:

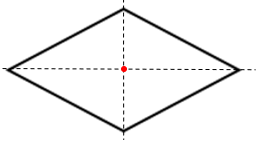
Bài 3. Hình nào sau đây có trục đối xứng?

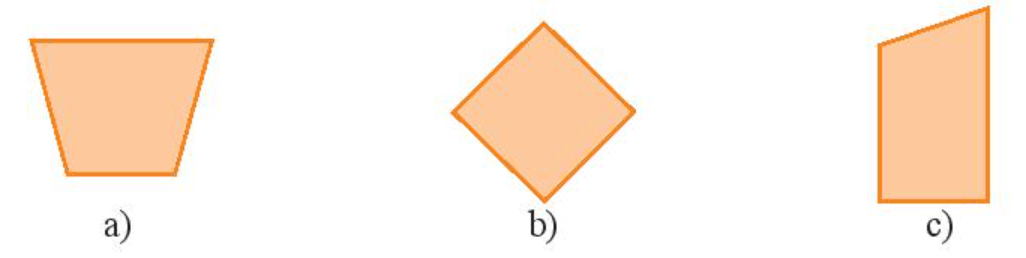
Lời giải:

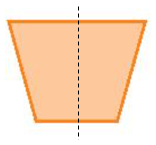
Hình a) có trục đối xứng (như hình vẽ).

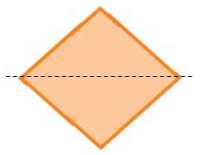
Hình b) có trục đối xứng (như hình vẽ).

Hình c) không có trục đối xứng.

Vậy trong ba hình trên chỉ có hình a) và hình b) có trục đối xứng.

Bài 4. Mỗi hình sau đây có bao nhiêu trục đối xứng? 

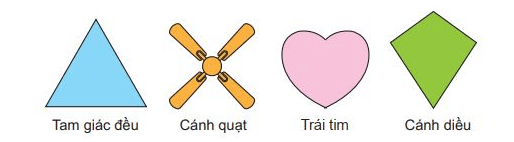
Lời giải:

Số các trục đối xứng của các hình được biểu diễn như sau:

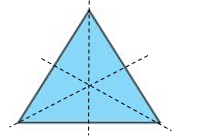
- Hình tam giác đều có 3 trục đối xứng.

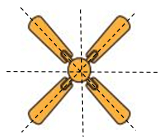
- Hình cánh quạt có 4 trục đối xứng.

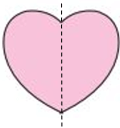
- Hình trái tim có 1 trục đối xứng.

- Hình cánh diều có 1 trục đối xứng.

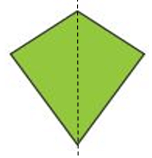
Bài 5. Hình nào sau đây có trục đối xứng.

Lời giải:

- Hình bông hoa tuyết có trục đối xứng (như hình vẽ).

- Hình hoa thức có trục đối xứng (như hình vẽ).

- Hình lá dương xỉ không có trục đối xứng.

Vậy trong ba hình trên chỉ có hình bông hoa tuyết và hoa thức có trục đối xứng.

Bài 6. Hình nào dưới đây có tâm đối xứng?

Lời giải:

- Hình a) có tâm đối xứng (như hình vẽ).

- Hình b) không có tâm đối xứng.

- Hình c) có tâm đối xứng (như hình vẽ).

- Hình d) không có tâm đối xứng.