Lý thuyết Tính chất cơ bản của phân số (Chân trời sáng tạo 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 2: Tính chất cơ bản của phân số

Video giải Toán 6 Bài 2: Tính chất cơ bản của phân số – Chân trời sáng tạo

A. Lý thuyết  Tính chất cơ bản của phân số

1. Tính chất 1

Tính chất 1: Nếu nhân cả tử số và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.

Ví dụ 1. Cho phân số 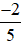. Nhân cả tử và mẫu của phân số  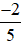với 3, ta được:

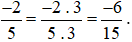
Khi đó, ta có phân số mới là 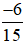 bằng phân số đã cho là .

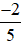Nhận xét: Có thể biểu diễn số nguyên ở dạng phân số với mẫu số (khác 0) tùy ý.

- Áp dụng tính chất 1, ta có thể quy đồng mẫu số hai phân số bằng cách nhân tử và mẫu mỗi phân số với số nguyên thích hợp.

Ví dụ 2. Có thể biểu diễn số −8 ở dạng phân số có mẫu số là 3 như sau:

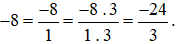
Ví dụ 3. Quy đồng mẫu số hai phân số .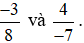

Lời giải: 

Quy đồng mẫu số hai phân số ta thực hiện như sau:

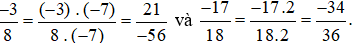
Nhận xét: Mẫu số giống nhau ở hai phân số là −56 còn gọi là mẫu số chung của hai phân số.

Khi quy đồng mẫu số hai phân số, có thể có nhiều cách chọn mẫu số chung.

Chú ý: Có thể quy đồng mẫu số của nhiều phân số bằng cách tìm mẫu số chung của nhiều phân số.

Ví dụ 4. Quy đồng mẫu số của ba phân số .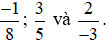

Lời giải: 

Quy đồng mẫu số ba phân số, ta nhân cả tử và mẫu của mỗi phân số nhân với tích hai mẫu số của hai phân số còn lại.

Ta thực hiện như sau:

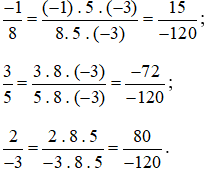
Mẫu số chung của ba phân số trên là −120.

2. Tính chất 2

Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.

Ví dụ 5. Cho phân số 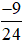. Chia cả tử và mẫu của phân số  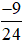cho 3, ta được:

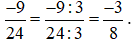
Khi đó, ta có phân số mới là 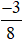 bằng phân số đã cho là .

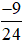Áp dụng tính chất 2, ta có thể rút gọn phân số bằng cách chia cả tử và mẫu cho cùng ước chung khác 1 và −1.

Ví dụ 6. Rút gọn phân số .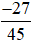

Lời giải: 

Chia cả tử và mẫu của phân số 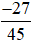 cho 9, ta được:

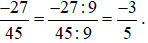
Nhận xét: Sau khi rút gọn ta được phân số mới là 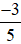 bằng phân số đã cho là .

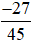Chú ý: Khi rút gọn phân số, có thể được nhiều kết quả, nhưng các phân số ở các kết quả đó đều bằng nhau.

Ví dụ 7. Rút gọn phân số .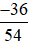

Lời giải: 

Chia cả tử và mẫu của phân số 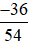 cho 2, ta được:

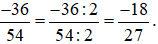
Chia cả tử và mẫu của phân số 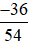 cho 3, ta được:

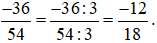
Chia cả tử và mẫu của phân số 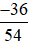 cho 6, ta được:

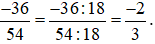
Nhận xét: Khi rút gọn phân số 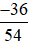, ta thu được nhiều kết quả như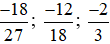  

Các phân số 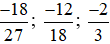 đều bằng nhau.

Tổng quát: .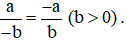

Chú ý: Mỗi phân số đều có nhiều phân số bằng nó.

Ví dụ 8. Viết phân số 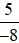 thành phân số có mẫu dương.

Lời giải: 

Phân số 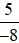 có mẫu là số nguyên âm. 

Do đó để viết phân số 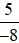 thành phân số có mẫu dương thì ta chia cả tử và mẫu của phân số này cho cùng một số nguyên âm và là ước chung của 5 và (−8) là (−1).

Khi đó ta có:

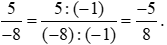
Vậy phân số 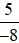 được viết thành phân số có mẫu dương là . 

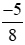B. Bài tập tự luyện 

Bài 1. Đưa mỗi phân số sau về phân số có mẫu số dương rồi quy đồng các phân số sau:

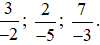
Lời giải: 

Đưa các phân số trên về phân số có mẫu số dương như sau:

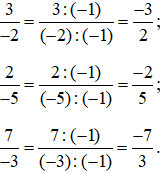
Quy đồng các phân số trên ta được:

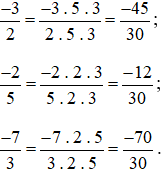
Bài 2. Áp dụng tính chất 1 và tính chất 2 để tìm một phân số bằng mỗi phân số sau:

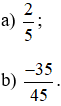
Lời giải:

a) Ta có thể nhân cả tử và mẫu của phân số 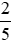 với một số nguyên khác 0 bất kỳ để được phân số mới bằng phân số đã cho (theo tính chất 1).

Chẳng hạn: Nhân cả tử và mẫu của phân số 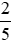 với 4, ta được:

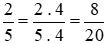 (theo tính chất 1).

Vậy một phân số bằng phân số .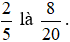 

b) Ta có thể chia cả tử và mẫu của một phân số 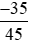 cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho (theo tính chất 2).

Chẳng hạn: Chia cả tử và mẫu của phân số 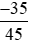 cho 5, ta được:

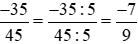 (theo tính chất 2).

Vậy một phân số bằng phân số .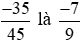

Bài 3. Rút gọn các phân số sau:

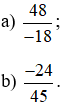
Lời giải: 

a) Chia cả tử và mẫu của phân số 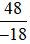 cho 6, ta được:

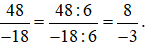
b) Chia cả tử và mẫu của phân số 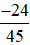 cho 3, ta được:

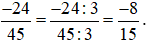
Bài 4. Dùng phân số có mẫu số dương nhỏ nhất để biểu thị xem số phút sau đây chiếm bao nhiêu phần của một giờ?

a) 36 phút;

b) 25 phút;

Lời giải:

Đổi: 1 giờ = 60 phút.

Để tìm phân số biểu thị số phút chiếm bao nhiêu phần của một giờ, ta lấy số phút chia cho 60.

a) Phân số biểu thị 36 phút chiếm số phần của một giờ là .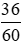

Rút gọn phân số, ta được: .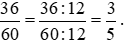

Vậy phân số có mẫu số dương nhỏ nhất để biểu thị 36 phút là 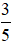 giờ.

b) Phân số biểu thị 25 phút chiếm số phần của một giờ là .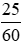

Rút gọn phân số, ta được: .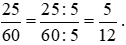

Vậy phân số có mẫu số dương nhỏ nhất để biểu thị 25 phút là 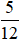 giờ.