Lý thuyết So sánh phân số (Chân trời sáng tạo 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 3: So sánh phân số

Video giải Toán 6 Bài 3: So sánh phân số – Chân trời sáng tạo

A. Lý thuyết So sánh phân số

1. So sánh hai phân số có cùng mẫu

Quy tắc 1. Với hai phân số có cùng một mẫu dương: Phân số nào có tử số nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

Ví dụ 1. So sánh .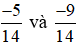

Lời giải:

Ta có −5 > −9 và 14 > 0 nên .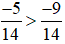

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

Ví dụ 2. So sánh .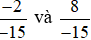

Lời giải:

Đưa hai phân số về cùng mẫu dương, ta được:

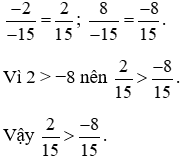
2. So sánh hai phân số khác mẫu

Quy tắc 2. Để so sánh hai phân số có mẫu khác nhau, ta viết hai phân số đó ở dạng hai phân số có cùng một mẫu dương rồi so sánh hai phân số mới nhận được.

Ví dụ 3. So sánh .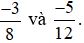

Lời giải:

Mẫu số chung = BCNN (8; 12) = 24.

Ta thực hiện 

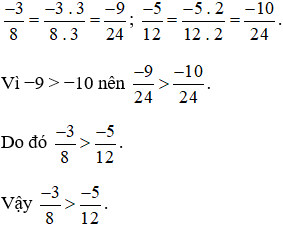
3. Áp dụng quy tắc so sánh phân số

Nhờ viết số nguyên dưới dạng phân số, ta so sánh được số nguyên với phân số.

Ví dụ 4. Viết số nguyên dưới dạng phân số rồi so sánh hai số sau: 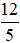 và 3.

Lời giải:

a) Ta có: .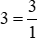

Mẫu số chung là: 5.

Ta thực hiện: 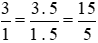 và giữ nguyên phân số .

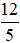Vì 15 > 12 nên

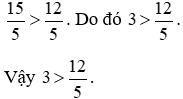
Chú ý: Khi so sánh phân số ta có thể áp dụng tính chất bắc cầu. Nghĩa là: 

Nếu có 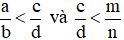 thì ta có .

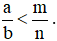Ví dụ 5. So sánh .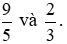

Lời giải: 

Phân số 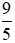 có tử số là 9 lớn hơn mẫu số là 5 nên .

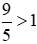Phân số 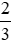 có tử số là 2 nhỏ hơn mẫu số là 3 nên .

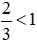Do đó .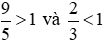

Theo tính chất bắc cầu, ta suy ra:

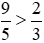
Nhận xét: 

- Phân số nhỏ hơn số 0 gọi là phân số âm. Phân số lớn hơn số 0 là phân số dương.

- Theo tính chất bắc cầu, phân số âm nhỏ hơn phân số dương.

Ví dụ 6. So sánh  .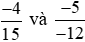

Lời giải: 

Ta có: 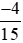 là phân số âm vì phân số có tử số và mẫu số trái dấu nên .

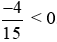Và 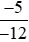 là phân số dương vì phân số có tử số và mẫu số cùng dấu nên .

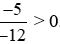Áp dụng tính chất bắc cầu, ta suy ra:  .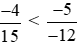

Vậy .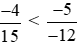

B. Bài tập tự luyện

Bài 1. Sắp xếp các số theo thứ tự tăng dần: .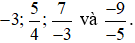

Lời giải:

Để sắp xếp các phân số theo thứ tự tăng dần, ta làm như sau:

Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.

- Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.

- Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.

Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).

Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần (phân số âm luôn bé hơn phân số dương).

Ta có .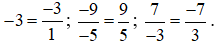

+ Các phân số dương: .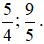

+ Các phân số âm: .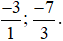

Ta so sánh các phân số dương với nhau, các phân số âm với nhau:

+ So sánh .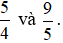

Mẫu số chung: 20.

Ta thực hiện: .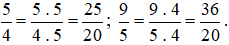

Vì 25 < 36 nên .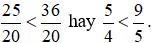

+ So sánh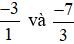 

Mẫu số chung: 3.

Ta thực hiện: 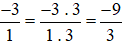 và giữ nguyên phân số .

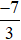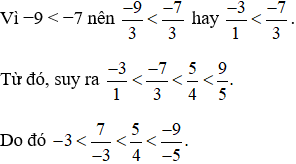
Vậy ta sắp xếp được theo thứ tự tăng dần như sau: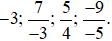 

Bài 2. So sánh hai phân số.

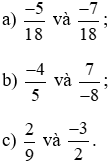
Lời giải:

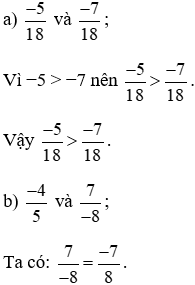
Quy đồng hai phân số 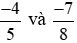 ta thực hiện: 

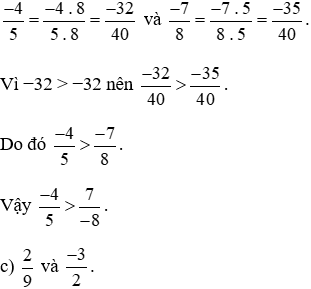
Ta có 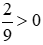 (vì phân số này là phân số dương).

Và 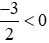 (vì phân số này là phân số âm).

Theo tính chất bắc cầu, phân số dương lớn hơn phân số âm nên .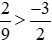

Vậy .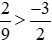

Bài 3. So sánh 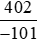 và −4.

Lời giải:

Cách 1: Đưa số nguyên và phân số về dạng phân số có cùng mẫu số dương, rồi so sánh tử số của hai phân số.

Ta có: 

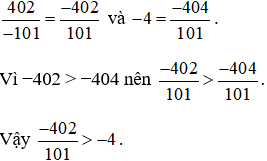
Cách 2: Đưa số nguyên về dạng phân số có mẫu số là 1, tử số là số nguyên đó, sau đó quy đồng mẫu số hai phân số đó (đưa hai phân số về cùng mẫu số dương).

Ta có: .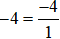

Quy đồng mẫu số hai phân số 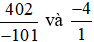, ta được:

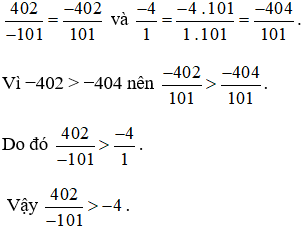
Bài 4. Bình đọc hết một quyển sách trong 3 ngày. Ngày thứ nhất đọc được  quyển sách, ngày thứ hai đọc được 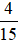 quyển sách, ngày thứ ba đọc được  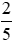quyển sách. Hỏi trong ba ngày đó thì ngày nào Bình đọc được nhiều nhất, ngày nào đọc được ít nhất?

Lời giải: 

Bài toán đưa về sắp xếp các phân số 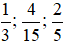 theo thứ tự tăng dần hoặc giảm dần. Sau đó kiểm tra xem ngày nào Bình đọc được nhiều nhất, ngày nào đọc được ít nhất.

Quy đồng mẫu số các phân số 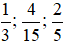 , ta được:

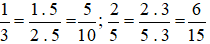 giữ nguyên phân số .

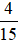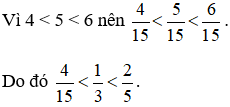
Vậy ngày thứ hai Bình đọc được nhiều nhất tương ứng với 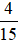 quyển sách, ngày thứ ba Bình đọc được ít nhất tương ứng với  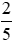quyển sách