Lý thuyết Số tự nhiên (Chân trời sáng tạo 2024) Toán 6

Lý thuyết Toán lớp 6 Chương 1: Số tự nhiên 

Video giải Toán 6 Chương 1: Số tự nhiên - Chân trời sáng tạo

A. Lý thuyết Toán lớp 6 Chương 1: Số tự nhiên 

1.Tập hợp, phần tử

Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.

Mối quan hệ giữa tập hợp và phần tử: Tập hợp chứa phần tử (nếu có) và phần tử nằm trong tập hợp.

Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.

2. Các kí hiệu tập hợp

- Người ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D, ... và sử dụng các chữ cái thường a, b, c, ... để kí hiệu cho phần tử.

- Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu chấm phẩy dấu “;”. Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.

- Phần tử x thuộc tập hợp A được kí hiệu là x $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ A, đọc là “x thuộc A”. Phần tử y không thuộc tập hợp A được kí hiệu là y $\notin$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\notin </span></span></span>$ A, đọc là “y không thuộc A”.

3. Các cách cho một tập hợp

Nhận xét. Để cho một tập hợp, thường có hai cách:

• Liệt kê các phần tử của tập hợp.

• Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

Ngoài 2 cách cho tập hợp như trên, người ta còn minh họa bằng hình vẽ (Sơ đồ Venn).

4. Tập rỗng

Tập rỗng là tập hợp không có phần tử nào, kí hiệu $\varnothing$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\varnothing </span></span></span>$.

5. Tập hợp N và N*

Các số 0; 1; 2; 3; 4; ... là các số tự nhiên.

Tập hợp các số tự nhiên được kí hiệu là N , tức là N = {0; 1; 2; 3; ...}.

Tập hợp các số tự nhiên khác 0 được kí hiệu là N*, tức là N* = {1; 2; 3; ...}

Tập hợp N bỏ đi số 0 thì được N*.

Khi cho một số tự nhiên x $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$N*  thì ta hiểu x là số tự nhiên khác 0.

6. Thứ tự trong tập hợp số tự nhiên

a) Biểu diễn các số tự nhiên trên tia số:

Các số tự nhiên được biểu diễn trên tia số bởi các điểm cách đều như sau:

- Tia số có mũi tên sang phải biểu thị chiều tăng dần của các số tự nhiên.

- Mỗi số tự nhiên được biểu diễn bằng một điểm trên tia số; điểm biểu diễn số tự nhiên n được gọi là điểm n.

- Điểm 0 được gọi là gốc.

b) So sánh hai số tự nhiên

- Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết a < b (đọc là a nhỏ hơn b) hoặc b > a (đọc là b lớn hơn a).

- Khi biểu diễn trên tia số nằm ngang có chiều từ trái sang phải, nếu a < b thì điểm a nằm bên trái điểm b.

Ngoài ra ta cũng viết a ≥ b để chỉ a > b hoặc a = b.

+ Nếu a < b và b < c thì a < c (Tính chất bắc cầu).

+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.

+ Số 0 là số tự nhiên bé nhất.

7. Ghi số tự nhiên

a) Cách ghi số tự nhiên trong hệ thập phân

Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.

Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó.

Chú ý: Khi viết các số tự nhiên, ta quy ước:

- Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.

- Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.

- Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau.

b) Hệ thập phân

Ta đã biết cấu tạo thập phân của một số:

- Kí hiệu 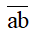 chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a (a ≠ 0) và chữ số hàng đơn vị là b.

Ta có: 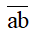 = a × 10 + b.

- Kí hiệu 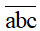 chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là a (a ≠ 0), chữ số hàng chục là b, chữ số hàng đơn vị là c.

Ta có: 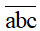 = a × 100 + b × 10 + c.

- Với các số cụ thể thì không viết dấu gạch ngang ở trên.

c) Hệ La Mã

Cách ghi số La Mã như sau:

Chữ số	I	V	X
Giá trị tương ứng trong hệ thập phân	1	5	10

Ghép các chữ số I, V, X với nhau ta có thể được số mới. Dưới đây là bảng chuyển đổi La Mã sang số trong hệ thập phân tương ứng (từ 1 đến 10):

Số La Mã	I	II	III	IV	V	VI	VII	VIII	IX	X
Giá trị tương ứng trong hệ thập phân	1	2	3	4	5	6	7	8	9	10

Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X

XI	XII	XIII	XIV	XV	XVI	XVII	XVIII	XIX	XX
11	12	13	14	15	16	17	18	19	20

Các số La Mã biểu diễn các số từ 21 đến 30: Thêm XX vào bên trái mỗi số từ I đến X

Chú ý:

- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.

- Không có số La Mã nào biểu diễn số 0.

8. Phép cộng và phép nhân

Phép cộng (+) và phép nhân (×) các số tự nhiên đã được biết đến ở tiểu học.

Chú ý: Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số ta có thể không viết dấu nhân ở giữa các thừa số; dấu “×” trong tích các số cũng có thể thay bằng dấu “.”.

Ví dụ:

• m × n có thể viết là m . n hay mn;

• 5 × x × y có thể viết là 5 . x . y hay 5xy;

• 125 × 731 có thể viết là 125 . 731.

9. Tính chất của phép cộng và phép nhân số tự nhiên

Với a, b, c là các số tự nhiên, ta có:

− Tính chất giao hoán:

a + b = b + a

a . b = b . a

− Tính chất kết hợp:

(a + b) + c = a + (b + c)

(a . b) . c = a . (b . c)

− Tính chất phân phối của phép nhân đối với phép cộng:

a . (b + c) = a . b + a . c

− Tính chất cộng với số 0, nhân với số 1:

a + 0 = a

a . 1 = a.

10. Phép trừ và phép chia hết

Ở Tiểu học ta đã biết cách tìm x trong phép toán b + x = a; trong đó a, b, x là các số tự nhiên, a ≥ b.

Nếu có số tự nhiên x thỏa mãn b + x = a, ta có phép trừ a – b = x và gọi x là hiệu quả của phép trừ số a cho số b, a là số bị trừ, b là số trừ.

Tương tự với a, b là các số tự nhiên, b ≠ 0, nếu có số tự nhiên x thỏa mãn bx = a, ta có phép chia a : b = x và gọi a là số bị chia, b là số chia, x là thương của phép chia số a cho số b.

Chú ý: Phép nhân cũng có tính chất phân phối đối với phép trừ:

a . (b − c) = a . b – a . c (b > c)

11. Lũy thừa

Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.

an = a . a ….. a (n thừa số a) (n $\notin$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\notin </span></span></span>$N* )

Ta đọc an là “a mũ n” hoặc “lũy thừa bậc n của a”.

Số a được gọi là cơ số, n được gọi là số mũ.

Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.

Đặc biệt, a2 còn được đọc là “a bình phương” hay “bình phương của a”.

a3 được đọc là “a lập phương” hay “lập phương của a”.

Quy ước: a1 = a.

12. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

am . an = am + n.

13. Chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.

am : an = am – n (a ≠ 0; m ≥ n ≥ 0).

Quy ước: a0 = 1 (a ≠ 0).

14. Thứ tự thực hiện phép tính

Khi thực hiện các phép tính trong một biểu thức:

− Đối với biểu thức không có dấu ngoặc:

+ Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.

+ Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

− Đối với biểu thức có dấu ngoặc:

+ Nếu biểu thức có các dấu ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính trong dấu ngoặc tròn trước, rồi thực hiện phép tính trong dấu ngoặc vuông, cuối cùng thực hiện phép tính trong dấu ngoặc nhọn.

15. Sử dụng máy tính cầm tay

− Nút mở máy:  

 − Nút tắt máy:  

− Các nút số từ 0 đến 9.

− Nút dấu cộng, dấu trừ, dấu nhân, dấu chia.

− Nút dấu “=” cho phép hiện ra kết quả trên màn hình số.

− Nút xóa (xóa số vừa đưa vào bị nhầm):  

− Nút xóa toàn bộ phép tính (và kết quả) vừa thực hiện:  

− Nút dấu ngoặc trái và phải:  

− Nút tính lũy thừa: 

16. Chia hết và chia có dư

Cho hai số tự nhiên a và b, trong đó b khác 0. Ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó 0 ≤ r < b. Ta gọi q và r lần lượt là thương và số dư trong phép chia a cho b.

− Nếu r = 0 tức a = b . q, ta nói a chia hết cho b, kí hiệu a ⋮ b và ta có phép chia hết a : b = q . a

− Nếu r ≠ 0, ta nói a không hết cho b, kí hiệu a ⋮̸ b và ta có phép chia có dư.

17. Tính chất chia hết của một tổng

Tính chất 1

Cho a, b, n là các số tự nhiên, n khác 0.

Nếu a ⋮ n và b ⋮ n thì (a + b) ⋮ n và (a − b) ⋮ n (a ≥ b)

Nếu a ⋮ n, b ⋮ n và c ⋮ n thì (a + b + c) ⋮ n.

Tính chất 2

Cho a, b, n là các số tự nhiên, n khác 0 (a ≥ b).

Nếu a ⋮̸ n và b ⋮ n thì (a + b) ⋮̸ n và (a − b) ⋮̸ n.

Nếu a ⋮ n và b ⋮̸ n thì (a + b) ⋮̸ n và (a − b) ⋮̸ n.

Nếu a ⋮̸ n, b ⋮ n và c ⋮ n thì (a + b + c) ⋮̸ n.

Nếu trong một tổng chỉ có đúng một số hạng không chia hết cho một số, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đó.

18. Dấu hiệu chia hết cho 2

Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

19. Dấu hiệu chia hết cho 5

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

20. Dấu hiệu chia hết cho 9

Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.

21. Dấu hiệu chia hết cho 3

Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.

22. Ước và bội

Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.

Tập hợp các ước của a được kí hiệu là Ư(a). Tập hợp các bội của a được kí hiệu là B(a).

Chú ý:

- Số 0 là bội của tất cả các số tự nhiên khác 0. Số 0 không là ước của bất kì số tự nhiên nào.

- Số 1 chỉ có một ước là 1. Số 1 là ước của mọi số tự nhiên.

- Mọi số tự nhiên a lớn 1 luôn có ít nhất hai ước là 1 và chính nó.

23. Cách tìm ước

Cách tìm Ư(a):

Ta có thể tìm các ước của a (a > 1), ta có thể lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.

24. Cách tìm bội

Cách tìm B(a):

Muốn tìm bội của số tự nhiên a khác 0, ta có thể nhân a lần lượt với 0, 1, 2, 3, ...

Chú ý:

Bội của a có dạng tổng quát là a . k với k $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$N. Ta có thể viết:

$B\left(a\right)=\{a.k|k\in N\}$$\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">(</span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">)</span></span></span><span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">=</span></span></span><span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\{</span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}\text{<span style="font-size:18px;"><span style="font-size:10px;"><span style="line-height:2;">\hspace{0.17em}\hspace{0.17em}</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">.</span></span></span>\text{<span style="font-size:18px;"><span style="font-size:10px;"><span style="line-height:2;">\hspace{0.17em}\hspace{0.17em}</span></span></span>}\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">|</span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\mathbb{N}</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\}</span></span></span>$.

25. Số nguyên tố. Hợp số

− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

− Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn hai ước.

Ví dụ:

+ Số 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.

+ Số 15 có bốn ước là 1; 3; 5; 15 nên 15 là hợp số.

Lưu ý: Số 0 và số 1 không là số nguyên tố cũng không là hợp số.

26. Phân tích một số ra thừa số nguyên tố

a. Thế nào là phân tích một số ra thừa số nguyên tố?

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Chú ý:

− Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.

− Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.

− Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.

b. Cách phân tích một số ra thừa số nguyên tố

Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc.

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Chú ý: Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.

Cách 2: Phân tích một số ra thừa số nguyên tố theo sơ đồ cây.

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

27. Ước chung

- Một số được gọi là ước chung của hai hay nhiều số nếu nó là ước của tất cả các số đó.

- Tập hợp các ước chung của hai số a và b kí hiệu là ƯC(a, b).

x $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ ƯC(a, b) nếu a ⋮ x và b ⋮ x.

- Tương tự, tập hợp các ước chung của a, b, c kí hiệu là ƯC(a, b, c).

x $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ ƯC(a, b, c) nếu a ⋮ x, b ⋮ x và c ⋮ x.

Cách tìm ước chung của hai số a và b:

- Viết tập hợp các ước của a và của b: Ư(a), Ư(b).

- Tìm những phần tử chung của Ư(a) và Ư(b).

28. Ước chung lớn nhất

Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Kí hiệu ước chung lớn nhất của a và b là ƯCLN(a, b).

Tương tự, ước chung lớn nhất của a, b và c là ƯCLN(a, b, c).

Nhận xét: Tất cả các ước chung của hai hay nhiều số đều là ước của ƯCLN của các số đó.

Ví dụ:

ƯC(16, 24) = {1; 2; 4; 8} nên ƯCLN(16, 24) = 8, vì 8 là số lớn nhất trong số các ước chung của 16 và 24. Các ước chung của 36 và 45 là 1; 2; 4; 8 đều là ước của 8.

Nhận xét: Với mọi số tự nhiên a và b, ta có:

ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.

Ví dụ: ƯCLN(9, 1) = 1; ƯCLN(5, 18, 1) = 1.

29. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố

Quy tắc:

Muốn tìm ƯCLN của của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.

Chú ý: Hai số có ƯCLN bằng 1 gọi là hai số nguyên tố cùng nhau.

Ví dụ: ƯCLN(15; 23) = 1 nên 15 và 23 được gọi là hai số nguyên tố cùng nhau.

30. Ứng dụng trong rút gọn về số tối giản

Rút gọn phân số: Chia cả tử và mẫu cho ước chung khác 1 (nếu có) của chúng.

Phân số tối giản: a/b là phân số tối giản nếu ƯCLN(a, b) = 1.

Đưa một phân số chưa tối giản về phân số tối giản:

Chia cả tử và mẫu cho ƯCLN(a, b).

31. Bội chung

Một số được gọi là bội chung của hai hay nhiều số nếu nó là bội của tất cả các số đó.

• Kí hiệu tập hợp các bội chung của a và b là BC(a, b).

• Tương tự, tập hợp các bội chung của a, b, c là BC(a, b, c).

Cách tìm bội chung của hai số a và b:

- Viết tập hợp B(a) và bội B(b).

- Tìm những phần tử chung của B(a) và B(b).

32. Bội chung nhỏ nhất

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu bội chung nhỏ nhất của a và b là BCNN(a, b).

Tương tự, bội chung nhỏ nhất của a, b và c là BCNN(a, b, c).

Nhận xét: Tất cả các bội chung của a và b đều là bội của BCN(a, b). Mọi số tự nhiên đều là bội của 1.

Do đó, với mọi số tự nhiên a và b (khác 0) ta có:

BCNN(a, 1) = a;

BCNN(a, b, 1) = BCNN(a, b).

33. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố

Quy tắc:

Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Chú ý:

• Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.

• Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.

34. Ứng dụng trong quy đồng mẫu các phân số

Quy tắc:

Muốn quy đồng mẫu số nhiều phân số ta có thể làm như sau:

Bước 1: Tìm một bội chung của các mẫu số (thường là BCNN) để làm mẫu số chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu số (bằng cách chia mẫu số chung cho từng mẫu số riêng).

Bước 3: Nhân tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.

B. Bài tập tự luyện

Bài 1. Điền số thích hợp vào ô trống.

Số tự nhiên	21		14		19
Số La Mã		XVI		XXV

Hướng dẫn giải

+ Số 1 được viết là I.

Số 21 = 1 + 20, tức là số 1 thêm 20 đơn vị nên ta thêm XX trước I được XXI.

Do đó số 21 được viết thành số La Mã là XXI.

+ Số XVI có 3 thành phần là X, V, I tương ứng với các giá trị 10; 5; 1.

Ta có 10 + 5 + 1 = 16.

Do đó số XVI biểu diễn số 16.

+ Số 4 được viết là IV.

Số 14 = 4 + 10, tức là số 4 thêm 10 đơn vị nên ta thêm X trước IV được XIV.

Do đó số 14 được viết thành số La Mã là XIV.

+ Số XXV có 3 thành phần là X, X, V tương ứng với các giá trị 10; 10; 5.

Ta có 10 + 10 + 5 = 25.

Do đó số XXV biểu diễn số 25.

+ Số 9 được viết là IX.

Số 19 = 9 + 10, tức là số 4 thêm 10 đơn vị nên ta thêm X trước IX được XIX.

Do đó số 19 được viết thành số La Mã là XIX.

Vậy ta có bảng sau:

Số tự nhiên	21	16	14	25	19
Số La Mã	XXI	XVI	XIV	XXV	XIX

Bài 2. Tìm số tự nhiên x để số 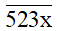 chia hết cho 3 và chia cho 2 dư 1.

Hướng dẫn giải

Số tự nhiên chia cho 2 dư 1 nên x là số lẻ.

Để 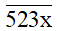 chia hết cho 3 thì:

(5 + 2 + 3 + x) ⋮ 3

Hay (10 + x) ⋮ 3

Suy ra x = 2; x = 5; x = 8.

Để 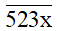 chia hết cho 3 và chia cho 2 dư 1 thì x = 5.

Vậy x = 5 thỏa mãn bài toán.

Bài 3. Cho E là tập hợp các số tự nhiên vừa lớn hơn 24 vừa nhỏ hơn 30. Điền kí hiệu $\in ,\notin$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span><span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">,</span></span></span><span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\notin </span></span></span>$ thích hợp vào ô trống dưới đây.

Hướng dẫn giải

Các số tự nhiên vừa lớn hơn 24 vừa nhỏ hơn 30 là: 25; 26; 27; 28; 29.

Vì 25 thuộc tập hợp E nên ta kí hiệu 25 $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ E.

Vì 5 không thuộc tập hợp E nên ta kí hiệu 5 $\notin$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\notin </span></span></span>$ E.

Vì 30 không thuộc tập hợp E nên ta kí hiệu 30 $\notin$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\notin </span></span></span>$ E.

Vì 28 thuộc tập hợp E nên ta kí hiệu 28 $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ E.

Vậy ta điền kí hiệu vào ô trống như sau:

Bài 4. Tập hợp M gồm tất cả các tháng (dương lịch) có 30 ngày. Hãy viết tập hợp M bằng cách liệt kê các phần tử của tập hợp.

Hướng dẫn giải
Các tháng dương lịch có 30 ngày gồm: tháng 4, tháng 6, tháng 9, tháng 11.

Vậy tập hợp M được viết bằng cách liệt kê các phần tử của tập hợp là:

M = {tháng 4; tháng 6; tháng 9; tháng 11}.

Bài 5. Cho tập hợp A gồm các số tự nhiên lớn hơn 4 nhưng không quá 10. Hãy viết tập hợp A bằng cách chỉ ra tính chất đặc trưng của tập hợp đó.

Hướng dẫn giải

Các phần tử của tập hợp A gồm các số tự nhiên lớn hơn 4 nhưng không quá 10.

Hay tập hợp A gồm các số tự nhiên lớn hơn 4 và nhỏ hơn hoặc bằng 10.

Tập hợp B gồm các phần tử là: 5; 6; 7; 8; 9; 10.

Vậy tập hợp B viết dưới dạng chỉ ra tính chất đặc trưng:

$\text{B={}x\in N|4<x\le 10\text{}}$$\text{<span style="font-size:18px;"><span style="font-size:10px;"><span style="line-height:2;">B\hspace{0.17em}=\hspace{0.17em}{</span></span></span>}\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\mathbb{N}</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">|</span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">4</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;"><</span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\le </span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">10</span></span></span>}\text{<span style="font-size:18px;"><span style="font-size:10px;"><span style="line-height:2;">}</span></span></span>}$.

Bài 6. Biểu diễn các số 1 342; 4 516; 6 515 trong hệ thập phân.

Hướng dẫn giải

Các số 1 342; 4 516; 6 515 được biểu diễn trong hệ thập phân như sau:

1 342 = 1 × 1 000 + 3 ×100 + 4 × 10 + 2;

4 516 = 4 × 1 000 + 5 ×100 + 1 × 10 + 6;

6 515 = 6 × 1 000 + 5 ×100 + 1 × 10 + 5.

Bài 7: Bạn Nam phải đánh số trang sách từ trang 20 đến trang 100. Vì sách cũ nên đã bị hỏng từ trang 41 đến trang 49. Hỏi Nam phải đánh tổng cộng bao nhiêu trang sách?

Hướng dẫn giải

Số trang sách Nam phải đánh khi sách không hỏng là:

100 – 20 + 1 = 81 (trang).

Số trang sách bị hỏng là:

49 – 41 + 1 = 9 (trang).

Số trang Nam phải đánh số là:

81 – 9 = 72 (trang).

Vậy Nam phải đánh tổng cộng 72 trang sách.

Bài 8: Số dân đầu năm 2021 của một thành phố là 13 924 dân. Đến tháng 8 năm 2021 thì tăng thêm 5 785 dân. Hỏi đầu năm 2022 thì số dân là bao nhiêu biết số dân tăng thêm từ tháng 8 năm 2021 đến cuối năm 2021 bằng 3/5 số dân tăng thêm từ đầu năm 2021 đến tháng 8 năm 2021?

Hướng dẫn giải

Số dân tăng thêm từ tháng 8 năm 2021 đến cuối năm 2021 là:

5 785 .  = 3 471 (người)

Số dân tăng thêm từ đầu năm 2021 đến cuối năm 2021 là:

5 785 + 3 471 = 9 256 (người)

Số dân đầu năm 2022 là:

13 924 + 9 256 = 23 180 (người)

Vậy đầu năm 2022 thì số dân của thành phố đó là 23180 người.

Bài 9. Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa.

a) x . x8 ;

b) 42 . 64;

c) 10 . 2 . 5.

Hướng dẫn giải

a) x . x8 = x1 . x8 = x1 + 8 = x9 ;

b) 42 . 64 = 42 . 4 . 4 . 4 = 42 . 43 = 42 + 3 = 45 ;

c) 10 . 2 . 5 = 10 . (2 . 5) = 10 . 10 = 102.

Bài 10. Tính 44 . 4 : 16 + 6.

Hướng dẫn giải

44 . 4 : 16 + 6

= 44 . 41 : 42 + 6

= 44 + 1 – 2 + 6

= 43 + 6

= 4 . 4 . 4 + 6

= 64 + 6 = 70.

Bài 11. Tìm x biết: (2x + 1)3 = 729.

Hướng dẫn giải

(2x + 1)3 = 729

(2x + 1)3 = 93

(2x + 1) = 9

2x + 1 = 9

2x = 9 – 1

2x = 8

x = 4.

Vậy x = 4.

Bài 12. Tính:

a) 514 – 122 +  43;

b) 52 . [4 . (23 + 142) – 623].

Hướng dẫn giải

a) 514 – 122 +  43

= 514 – 144 +  64

= 370 +  64

= 434.

b) 52 . [4 . (23 + 142) – 623]

= 52 . [4 . (23 + 196) – 623]

= 52 . [4 . 219 – 623]

= 52 . [876 – 623]

= 52 . 253

= 13 156.

Bài 13. Sử dụng máy tinh cầm tay, tính:

a) 93 . (4 237 – 1 928) + 2 500;

b) 53 . (64 . 19 + 26 . 35) – 210.

Hướng dẫn giải

a) Ấn nút: 

Kết quả: 217 237.

b) Ấn nút: 

Kết quả: 264 726.

Bài 14. Tìm x biết:

a) 8x – 6 = 50;

b) [43 – (18 . 12 – 25 . 8)]x = 26 + 98.

Hướng dẫn giải

a) 8x – 6 = 50

8x = 50 + 6

8x = 56

x = 7.

Vậy x = 7.

b) [43 – (18 . 12 – 25 . 8)]x = 26 + 98

[43 – (18 . 12 – 25 . 8)]x = 64 + 98

[43 – (216 – 200)]x = 64 + 98

[43 – 16]x = 162

27x = 162

x = 6.

Vậy x = 6.

Bài 15. Không tính tổng, hãy kiểm tra:

a) 6 + 9 + 15 có chia hết cho 3 không?

b) 75 + 12 có chia hết cho 15 không?

c) 10 + 15 + 12 có chia hết cho 3 không?

Hướng dẫn giải

a) Vì 6 ⋮ 3; 9 ⋮ 3; 15 ⋮ 3 nên (6 + 9 + 15) ⋮ 3.

Vậy 6 + 9 + 15 chia hết cho 3.

b) Vì 75 ⋮ 15 và 12 ⋮̸ 15 nên (75 + 12) ⋮̸ 15.

Vậy 75 + 12 không chia hết cho 15.

c) Vì 10 ⋮ 5; 15 ⋮ 5; 12 ⋮̸ 5 nên (10 + 15 + 12) ⋮̸ 5

Vậy 10 + 15 + 12 không chia hết cho 5.

Bài 16. Cho tổng M = 105 + 72 + x. Để M chia hết cho 3 thì x phải như thế nào?

Hướng dẫn giải

Vì 105 ⋮ 3; 72 ⋮ 3 nên để M = 105 + 72 + x chia hết cho 3 thì x ⋮ 3.

Vậy để M chia hết cho 3 thì x phải chia hết cho 3.

Bài 17. Tìm d để 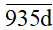 vừa chia hết cho 3 vừa chia hết cho 2.

Hướng dẫn giải

Điều kiện để d vừa chia hết cho 2 vừa chia hết cho 3 thì:

d là số chẵn và (9 + 3 + 5 + d) ⋮ 3.

Ta có: (9 + 3 + 5 + d) = 17 + d.

Để (17 + d) ⋮ 3 thì d = 1 hoặc d = 4.

Mà d là số chẵn nên d = 4.

Vậy để 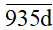 vừa chia hết cho 3 vừa chia hết cho 2 thì d = 4.

Bài 18. Từ ba số 2; 3; 7. Hãy ghép thành các số có ba chữ số khác nhau và chia hết cho 2.

Hướng dẫn giải

Số được ghép thành chia hết cho 2 nên phải có chữ số hàng đơn vị là 2.

Hai chữ số hàng chục có thể là 3 hoặc 7.

- Nếu chữ số hàng chục là 3 thì chữ số hàng trăm là 7.

Ta được số cần tìm là 732.

- Nếu chữ số hàng chục là 7 thì chữ số hàng trăm là 3.

Ta được số cần tìm là 372.

Vậy có hai số có thể ghép thành là 372 và 732.

Bài 19. Tìm b để số 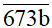 vừa chia hết cho 2 vừa chia hết cho 5?

Hướng dẫn giải

Để 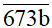 chia hết cho 2 thì b là số chẵn.

Để 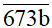 chia hết cho 5 thì b là 0 hoặc 5.

Do đó để 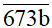 vừa chia hết cho 2 vừa chia hết cho 5 thì b = 0.

Vậy để 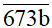 vừa chia hết cho 2 vừa chia hết cho 5 thì b = 0.

Bài 20. Có bao nhiêu số có hai chữ số chia hết cho 5.

Hướng dẫn giải

Các số có hai chữ số chia hết cho 5 là: 10; 15; 20; ….; 95.

Số các số có hai chữ số chia hết cho 5 là:

(95 – 10) : 5 + 1 = 18 (số)

Vậy có 18 số có hai chữ số chia hết cho 5.

Bài 21. Cho 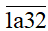 chia hết cho 9. Tìm số thay thế cho a.

Hướng dẫn giải

Tổng các chữ số của 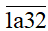 là 1 + a + 3 + 2 = a + 6 = a + 6.

Nên để 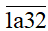 chia hết cho 9 thì a + 6 phải chia hết cho 9.

Do a là các số tự nhiên từ 0 đến 9 nên:

0 + 6 ≤ a + 6 ≤ 9 + 6.

Hay 6 ≤ a + 6 ≤ 15.

Số chia hết cho 9 từ 6 đến 15 chỉ có đúng một số là 9 nên a + 6 = 9

Do đó a = 3.

Vậy số thay thế cho a chỉ có thể là 3.

Bài 22: Cho 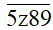 chia hết cho 3 và chia hết cho 9. Hãy tìm chữ số z.

Hướng dẫn giải

Vì một số bất kỳ nếu chia hết cho 9 thì cũng chia hết cho 3 nên ta chỉ xét 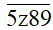 chia hết cho 9.

Để 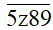 ⋮ 9 thì (5 + z + 8 + 9) ⋮ 9

Hay (22 + z) ⋮ 9 nên z = 5.

Vậy với z = 5 thì 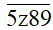 chia hết cho 3 và chia hết cho 9.

Bài 23. Tổng (hiệu) sau chia hết cho 3 hay 9?

a) 1251 + 5316;

b) 5436 – 1324;

c) 1 . 2 . 3 . 4 . 5 . 6 + 27.

Hướng dẫn giải

a) Tổng các chữ số của 1251 là 1 + 2 + 5 + 1 = 9 chia hết cho 3 và 9.

Tổng các chữ số của 5 316 là 5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.

Vậy 1251 + 5316 chia hết cho 3 nhưng không chia hết cho 9.

b) Tổng các chữ số của 5436 có 5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.

Tổng các chữ số của 1324 có 1 + 3 + 2 + 4 = 10 không chia hết cho 3 và 9.

Vậy 5436 – 1324 không chia hết cho 3 và 9.

c) Tích 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 (vì tích này có thừa số là 3).

Ta có: 1 . 2 . 3 . 4 . 5 . 6

= 1 . 2 . 3 . 4 . 5 . (3 . 2)

= 1 . 2 . 4 . 5 . (3 . 3) . 2

= 1 . 2 . 4 . 5 . 9 . 2 chia hết cho 9 (vì nó có thừa số là 9).

Do đó 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 và 9.

Tổng các chữ số của 27 là 2 + 7 = 9 chia hết cho 3 và 9.

Vậy 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 3 và 9.

Bài 24. Tìm các số tự nhiên a sao cho a $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ Ư(32) và a > 10.

Hướng dẫn giải

Ta có: Ư(32) = {1; 2; 4; 8; 16; 32}.

Mà a > 10 nên a $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ {16; 32}.

Vậy các số tự nhiên a sao cho a $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ Ư(32) và a > 10 là a = 16; a = 32.

Bài 25. Tìm số tự nhiên n để (5n + 14) ⋮ (n + 2).

Hướng dẫn giải

Ta có 5n + 14 = 5n + 10 + 4 = 5(n + 2) + 4.

Mà 5(n + 2) ⋮ (n + 2).

Do đó để (5n + 14) ⋮ (n + 2) thì 4 ⋮ (n + 2)

Khi đó (n + 2) ∈ Ư(4) = {1; 2; 4}.

+ Với n + 2 = 1. Không có số tự nhiên n thỏa mãn n + 2 = 1.

+ Với n + 2 = 2 thì n = 0.

+ Với n + 2 = 4 thì n = 2.

Vậy với n ∈ {0; 2} thì (5n + 14) ⋮ (n + 2).

Bài 26: Mỗi số sau là số nguyên tố hay hợp số? Giải thích.

a) 19;

b) 125;

c) 187;

d) 59.

Hướng dẫn giải

a) Vì 19 chỉ có đúng hai ước là 1 và chính nó nên 19 là số nguyên tố.

b) Vì 125 có ước là 5 khác 1 và chính nó nên 125 có nhiều hơn 2 ước. Do đó 125 là hợp số.

c) Vì 187 có ước là 11 khác 1 và chính nó nên 187 có nhiều hơn 2 ước. Do đó 187 là hợp số.

d) Vì 59 chỉ có đúng hai ước là 1 và chính nó nên 59 là số nguyên tố.

Bài 27: Phân tích mỗi số sau ra thừa số nguyên tố rồi cho biết mỗi số chia hết cho các số nguyên tố nào?

a) 40;

b) 144;

c) 300.

Hướng dẫn giải

a) Ta có:

40	2
20	2
10 5	2 5
1

Do đó 40 = 23 . 5.

Số 40 có thể chia hết cho các số nguyên tố là 2 và 5.

b) Ta có:

144	2
72	2
36 18 9 3	2 2 3 3
1

Do đó 144 = 24 . 32.

Số 144 có thể chia hết cho các số nguyên tố là 2 và 3.

c) Ta có:

300	2
150	2
75 25 5	3 5 5
1

Do đó 300 = 22 . 3 . 52.

Số 300 có thể chia hết cho các số nguyên tố là 2; 3 và 5.

Bài 28: Các số tự nhiên từ 1991 đến 2005 thì số nào là số nguyên tố?

Hướng dẫn giải

Các số tự nhiên từ 1991 đến 2005 là số nguyên tố:

− Ta loại bỏ các số chẵn: 1992; 1994; 1996; …; 2004.

− Loại bỏ tiếp các số chia hết cho 3: 1995; 2001.

− Ta còn phải xét các số 1991; 1993; 1997; 1999; 2003. Ta tìm số nguyên tố p mà p2 < 2005 là 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.

− Số 1991 chia hết cho 11 nên ta loại.

− Các số còn lại 1993, 1997, 1999, 2003 đều không chia hết cho các số nguyên tố trên.

Vậy từ 1991 đến 2005 chỉ có 4 số nguyên tố là 1993, 1997, 1999, 2003.

Bài 29: Tìm các ước chung lớn hơn 20 của 144 và 192.

Hướng dẫn giải

UCLN(144, 192) = 48.

Ước của 48 = {1; 2; 3; 4; 6; 8; 12; 24; 48}

Các ước của 48 lớn hơn 20 là 24 và 48.

Vậy các ước chung lớn hơn 20 của 144 và 192 là 24 và 48.

Bài 30. Một bác thợ mộc muốn làm kệ để đồ từ hai tấm gỗ dài 18 dm và 30 dm. Bác muốn cắt hai tấm gỗ này thành các thanh gỗ có cùng độ dài mà không để thừa mẩu gỗ nào. Em hãy giúp bác thợ mộc tìm độ dài lớn nhất có thể của mỗi thanh gỗ được cắt.

Hướng dẫn giải

Độ dài lớn nhất các thanh gỗ được cắt chính là ƯCLN của 18 và 30.

Ta có: 18 = 2 . 32; 30 = 2 . 3. 5.

Các thừa số nguyên tố chung là 2 và 3.

Số mũ lớn nhất của 2 là 1 và của 3 là 1.

Do đó ƯCLN(18; 30) = 2. 3 = 6.

Vậy độ dài lớn nhất có thể của các thanh gỗ được cắt là 6 dm.

Bài 31. Tìm hai số tự nhiên a, b, biết rằng: a + b = 162 và ƯCLN(a, b) = 18.

Lời giải

Giả sử a ≤ b.

Ta có: a + b = 162, ƯCLN(a, b) = 18.

Khi đó a ⋮ 18, b ⋮ 18.

Đặt a = 18m; b = 18n với ƯCLN(m, n) = 1, m ≤ n.

Từ a + b = 162 nên 18(m + n) = 162 suy ra m + n = 9.

Ta có ba cặp số (m; n) thỏa mãn m + n = 9 và ƯCLN(m, n) = 1, m ≤ n là:

(1; 8); (2; 7); (4; 5) (loại cặp số (3; 6) vì ƯCLN(3; 6) = 3 ≠ 1).

Ta có bảng sau:

m	1	2	4
n	8	7	5
a	18	36	72
b	144	126	90

Vậy các bộ hai số tự nhiên cần tìm là: (18; 144); (36; 126); (72; 90).

Bài 32: Tìm:

a) BC(6, 14);

b) BC(6, 20, 30);

c) BCNN(10, 1, 12).

Hướng dẫn giải

a) Phân tích 6 và 14 ra thừa số nguyên tố, ta được:

6 = 2 . 3; 14 = 2 . 7.

Khi đó, BCNN(6, 14) = 2 . 3 . 7 = 42.

Do đó BC(6, 14) = {0; 42; 84; 126; …}.

Vậy BC(6, 14) = B(42) = {0; 42; 84; 126; …}.

b) Phân tích 6; 20 và 30 ra thừa số nguyên tố, ta được:

6 = 2 . 3; 20 = 22 . 5; 30 = 2 . 3 . 5.

Khi đó, BCNN(6, 20, 30) = 22 . 3 . 5 = 60.

Do đó BC(6, 20, 30) = B(60) = {0; 60; 120; 180; …}.

Vậy BC(6, 20, 30) = {0; 60; 120; 180; …}.

c) Ta có: BCNN(10, 1, 12) = BCNN(10, 12).

Phân tích 10 và 12 ra thừa số nguyên tố, ta được:

10 = 2 . 5; 12 = 22 . 3.

Khi đó BCNN(10, 12) = 22 . 3 . 5 = 60.

Vậy BCNN(10, 1, 12) = BCNN(10, 12) = 60.

Bài 33: Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a ⋮ 126, a ⋮ 198.

Hướng dẫn giải

Vì a ⋮ 126 và a ⋮ 198 nên a là BC(126, 198).

Vì a là số tự nhiên nhỏ nhất nên a ∈ BCNN(126, 198).

Ta có: 126 = 2 . 32 . 7;

198 = 2 . 32 . 11.

Thừa số nguyên tố chung và riêng là 2; 3; 7 và 11.

Số mũ lớn nhất của 2 là 2, của 3 là 2, của là 7 và của 11 là 1.

BCNN(126, 198) = 2 . 32 . 7 . 11 = 1 386.

Vậy a = 1386.

Bài 34: Hai bạn Tùng và Hải thường đến thư viện đọc sách. Tùng cứ 8 ngày đến thư viện 1 lần, Hải 10 ngày 1 lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi ít nhất bao nhiêu ngày thì hai bạn cùng đến thư viện?

Hướng dẫn giải

Gọi a (ngày) là số ngày ít nhất hai bạn cùng đến thư viện ($x\in N$$\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>\mathrm{<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">�</span></span></span>}$, x ≥ 10).

Số ngày ít nhất hai bạn cùng đến thư viện thuộc bội chung nhỏ nhất của 8 và 10.

Khi đó, a $\in$$<span\; style="font-size:18px;"><span\; style="font-size:10px;"><span\; style="line-height:2;">\in </span></span></span>$ BCNN(8, 10).

Ta có: 8 = 23; 10 = 2 . 5

Do đó BCNN(8, 10) = 23 . 5 = 40 (thỏa mãn điều kiện).

Vậy sau 40 ngày thì hai bạn cùng đến thư viện.