Lý thuyết Góc ở vị trí đặc biệt. Tia phân giác của một góc (Kết nối tri thức 2024) Toán 7
Tóm tắt lý thuyết Toán 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc ngắn gọn, chính xác sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 7.
Lý thuyết Toán lớp 7 Bài 8:Góc ở vị trí đặc biệt. Tia phân giác của một góc
A. Lý thuyết Góc ở vị trí đặc biệt. Tia phân giác của một góc
1. Góc ở vị trí đặc biệt
a) Hai góc kề bù
• Định nghĩa: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.
• Tính chất: Hai góc kề bù có tổng số đo bằng 180°.
Ví dụ:
+ Góc ^xOy và ^yOz có cạnh Oy chung; Ox và Oz là hai tia đối nhau. Do đó ^xOy và ^yOz được gọi là hai góc kề bù.
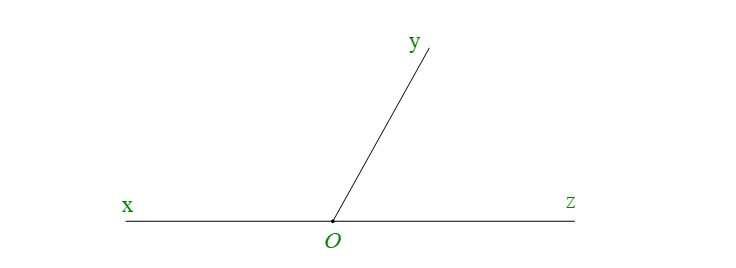
+ Vì ^xOy và ^yOz là hai góc kề bù nên ^xOy+^yOz=180°.
Chú ý:
• Hai góc kề bù được hiểu là hai góc vừa kề nhau, vừa bù nhau. Trong đó:
- Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía nhau đối với đường thẳng chứa cạnh chung đó.
Ví dụ: Trong hình vẽ dưới đây, góc mOt và góc nOt là hai góc kề nhau.
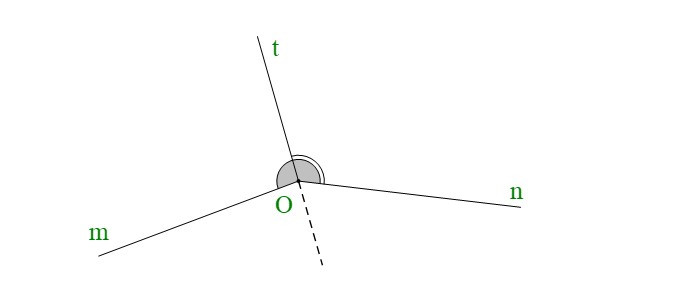
- Hai góc bù nhau là hai góc có tổng số đo bằng 180°.
Ví dụ: Trong hình vẽ dưới đây, có . Ta nói và là hai góc bù nhau.
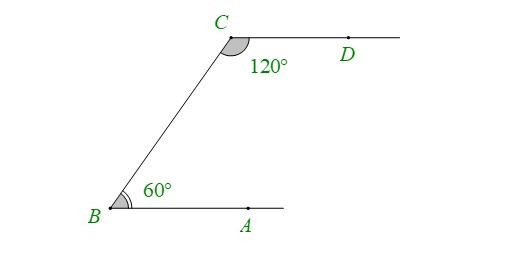
• Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa hai cạnh (hai tia) Ox và Oy của góc xOy. Khi đó ta có:
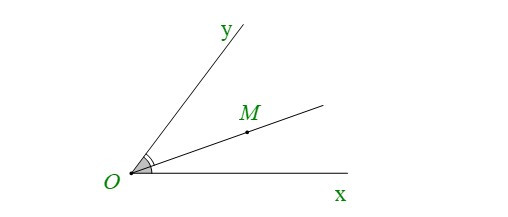
b) Hai góc đối đỉnh
• Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
• Tính chất: Hai góc đối đỉnh thì bằng nhau.
Ví dụ:
+ Hai đường thẳng , cắt nhau tại O. Khi đó và là hai tia đối nhau; và là hai tia đối nhau. Nên ta có các cặp góc đối đỉnh là: và ; và .
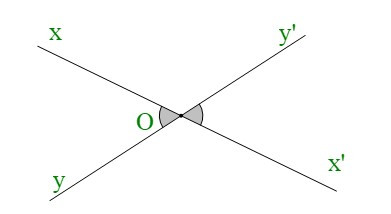
+ Có và là hai góc đối đỉnh thì ;
Ta lại có và là hai góc đối đỉnh thì .
Chú ý:
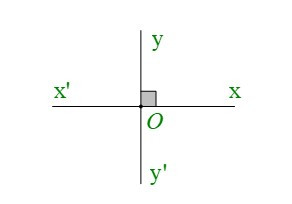
• Hai đường thẳng , cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc. Kí hiệu là: .
Ví dụ: Hai đường thẳng , cắt nhau tại O sao cho thì .
2. Tia phân giác của một góc
• Định nghĩa: Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
• Tính chất: Khi Oz là tia phân giác của góc xOy thì .
• Đường thẳng chứa tia phân giác của một góc gọi là đường phân giác của góc đó.
Ví dụ:
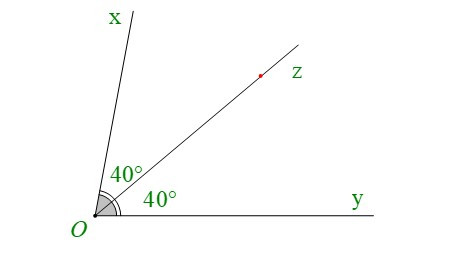
+ Cho và Oz là tia phân giác của góc xOy. Khi đó ta có:
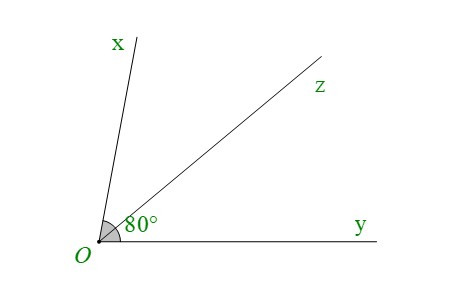
Chú ý:
• Cách vẽ tia phân giác của một góc:
Chẳng hạn: Vẽ tia phân giác Oz của
+ Vẽ góc .
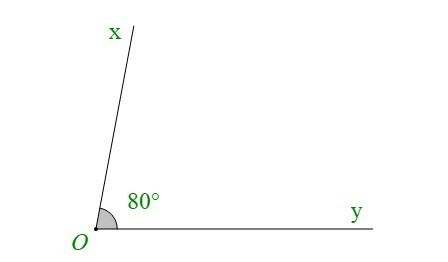
+ Oz là tia phân giác của góc xOy nên . Đánh dấu điểm ứng với vạch 40° của thước đo góc.
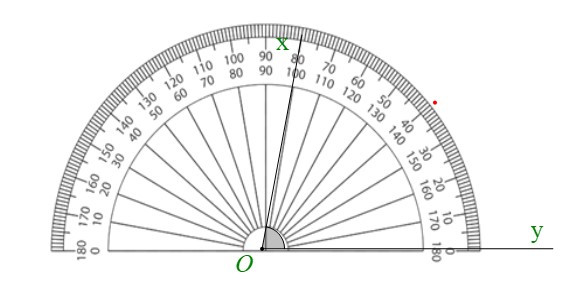
+ Kẻ Oz đi qua điểm đã đánh dấu. Ta được Oz là tia phân giác .
B. Bài tập tự luyện
B1. Bài tập trắc nghiệm
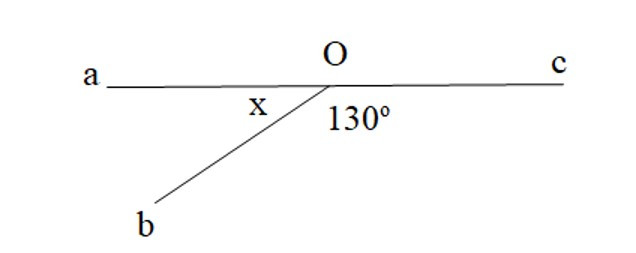
Bài 1. Tìm số đo x:
A. 65°;
B. 120°;
C. 95°;
D. 50°.
Hướng dẫn giải
Đáp án đúng là: D
Ta có góc aOb và góc bOc là hai góc kề bù nên .
Suy ra .
Vậy x = 50o.
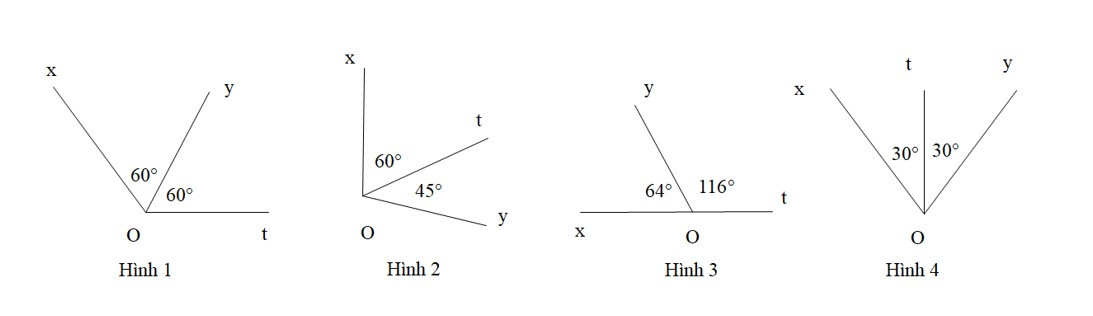
Bài 2. Tia Ot nào trong các hình dưới đây là tia phân giác của góc xOy.
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Hướng dẫn giải
Đáp án đúng là: D
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Hình 1 và hình 3 tia Ot không nằm trong góc nên tia Ot không phải tia phân giác của góc xOy.
Hình 2 có tia Ot nằm trong góc nhưng không tạo với hai cạnh của góc đó hai góc bằng nhau nên tia Ot trong hình 2 không phải tia phân giác của góc xOy.
Chỉ có hình 4 là tia Ot nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau nên Ot là tia phân giác của góc xOy.
Do đó chọn phương án D.
Bài 3. Chọn đáp án đúng.
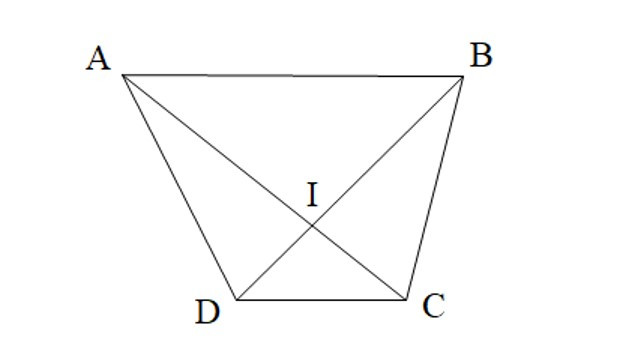
A. và là hai góc kề bù;
B. và là hai góc kề bù;
C. và là hai góc kề bù;
D. và là hai góc kề bù.
Hướng dẫn giải
Đáp án đúng là: C
và là hai góc hai góc kề bù (sai, vì và là hai góc hai góc đối đỉnh loại phương án A);
và là hai góc kề bù (sai, vì và là hai góc của tứ giác ABCD, loại phương án B);
và là hai góc kề bù (đúng, chọn phương án C);
và là hai góc kề bù (sai, vì và là hai góc đối đỉnh, loại phương án D).
B2. Bài tập tự luận
Bài 4. Vẽ góc xOy có số đo bằng 72°. Vẽ tia Om là tia đối của tia Ox.
a) Viết tên cặp góc kề bù trong hình vừa vẽ.
b) Tính số đo góc yOm.
c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.
Hướng dẫn giải
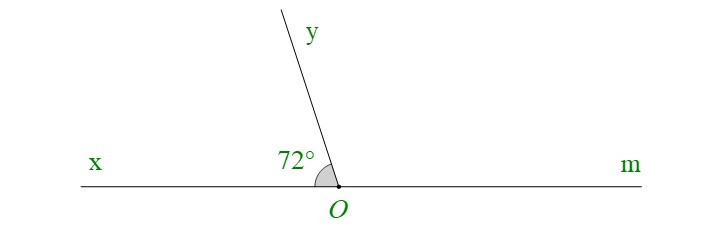
a) và có Oy chung; Om là tia đối của tia Ox.
và là hai góc kề bù.
b) Ta có: (hai góc kề bù)
Thay số:
Vậy:
c)
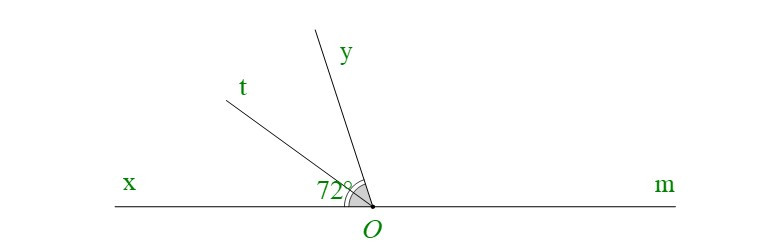
Vì Ot là tia phân giác của góc xOy nên:
Có: (hai góc kề bù)
Thay số:
Vậy: ; .
Bài 5. Cho hình vẽ dưới đây, biết . Tính số đo các góc còn lại trong hình vẽ.
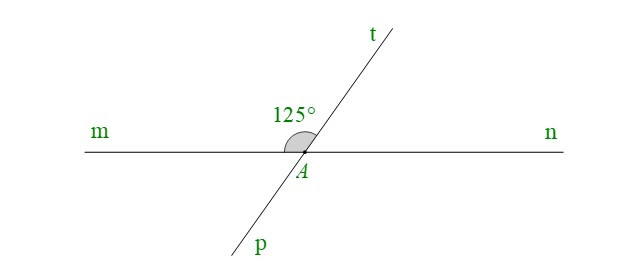
Hướng dẫn giải
Ta có: (hai góc đối đỉnh)
Ta có: (hai góc kề bù)
Thay số:
Lại có: (hai góc đối đỉnh)
Vậy: ; ; .
Bài 6. Cho hình vẽ dưới đây, hãy kể tên các cặp góc kề bù.
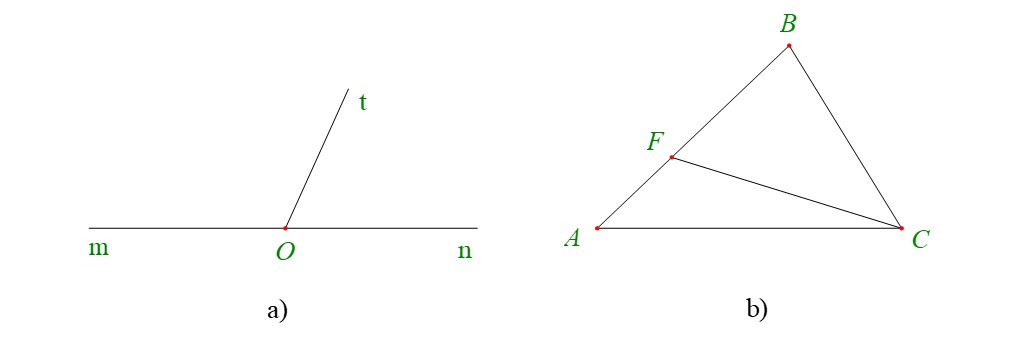
Hướng dẫn giải
a) Hai góc và có cạnh Ot chung; cạnh Om và On là hai tia đối nhau.
Nên và là cặp góc kề bù.
b) Hai góc và có cạnh FC chung; cạnh FA và FB là hai tia đối nhau.
Nên và là cặp góc kề bù.