Lý thuyết Tổng các góc trong một tam giác (Kết nối tri thức 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 12: Tổng các góc trong một tam giác

Lý thuyết Tổng các góc trong một tam giác

• Tổng ba góc trong một tam giác là tổng số đo ba góc trong tam giác đó.

• Tổng ba góc trong một tam giác bằng 180°.

• Góc ngoài của tam giác là góc kề bù với 1 góc của tam giác.

• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

Ví dụ:

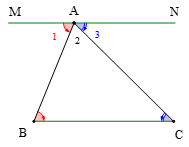
+ Cho tam giác ABC, ta có các góc A2; góc B; góc C là các góc trong của tam giác.

Qua A kẻ đường thẳng $MN\text{// BC}$. Khi đó ta có:

$\hat{B}=\widehat{A_1}$(hai góc so le trong)

$\hat{C}=\widehat{A_3}$(hai góc so le trong)

Mà $\widehat{A_1}+\widehat{A_2}+\widehat{A_3}=180°$

Nên: $\hat{B}+\widehat{A_2}+\hat{C}=180°$

Do đó tổng ba góc trong tam giác ABC bằng 180°.

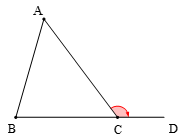
+ Trong hình dưới đây, ta thấy góc ACD kề bù với góc ACB (góc trong tam giác ABC). Do đó góc ACD gọi là góc ngoài của tam giác ABC.

Khi đó ta có: $\widehat{ACD}=\widehat{BAC}+\widehat{ABC}$.

Chú ý:

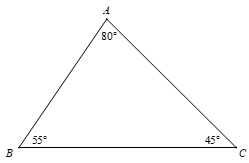
• Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

Ví dụ: Tam giác ABC có $\hat{A}=80°$; $\hat{B}=55°$; $\hat{C}=45°$. Như vậy các góc A; góc B; góc C đều là góc nhọn. Do đó tam giác ABC gọi là tam giác nhọn.

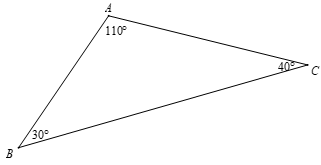
• Tam giác có một góc tù được gọi là tam giác tù.

Ví dụ: Tam giác ABC trong hình dưới đây có $\hat{A}=110°$là góc tù nên tam giác ABC gọi là tam giác tù.

• Tam giác có một góc vuông được gọi là tam giác vuông. Trong tam giác vuông, hai cạnh của góc vuông được gọi là cạnh góc vuông; cạnh còn lại được gọi là cạnh huyền.

• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.

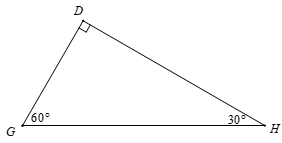
Ví dụ: Tam giác DGH có $\hat{D}=90°$ nên tam giác DGH gọi là tam giác vuông. Cạnh DG và DH gọi là cạnh góc vuông; cạnh GH là cạnh huyền. Góc G và góc H là hai góc phụ nhau.

Bài tập Tổng các góc trong một tam giác

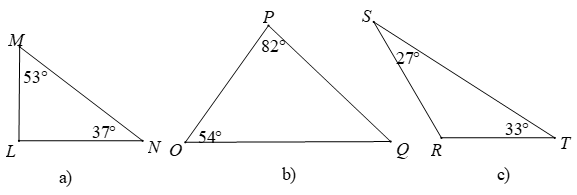
Bài 1. Trong các tam giác dưới đây. Tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?

Hướng dẫn giải

a) Tam giác MLN có: $\hat{M}+\hat{L}+\hat{N}=180°$ (tổng ba góc trong tam giác)

Do đó: $53°+\hat{L}+37°=180°$⟹$\hat{L}=180°-53°-37°=90°$

Như vậy góc L là góc vuông nên tam giác MLN là tam giác vuông.

b) Tam giác POQ có: $\hat{P}+\hat{O}+\hat{Q}=180°$ (tổng ba góc trong tam giác)

Do đó: $82°+54°+\hat{Q}=180°$⟹$\hat{Q}=180°-82°-54°=44°$< 90°

Như vậy góc Q; góc O; góc P là góc nhọn nên tam giác POQ là tam giác nhọn.

c) Tam giác SRT có: $\hat{S}+\hat{R}+\hat{T}=180°$ (tổng ba góc trong tam giác)

Do đó: $27°+\hat{R}+33°=180°$⟹$\hat{R}=180°-27°-33°=120°$> 90°

Như vậy góc R là góc tù nên tam giác SRT là tam giác tù.

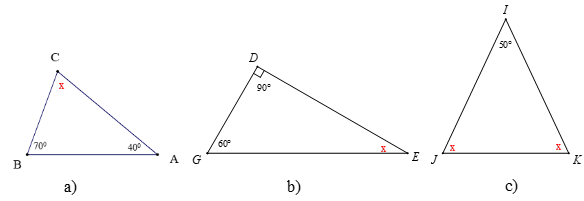
Bài 2. Tính số đo x trong các hình dưới đây:

Hướng dẫn giải

a) Tam giác ABC có: $\hat{A}+\hat{B}+\hat{C}=180°$ (tổng ba góc trong tam giác)

Do đó: $40°+70°+x=180°$

$x=180°-40°-70°$

$x=70°$

Vậy $x=70°$

b) Tam giác DGE có: $\hat{D}+\hat{G}+\hat{E}=180°$ (tổng ba góc trong tam giác)

Do đó: $90°+60°+x=180°$

$x=180°-90°-60°$

$x=30°$

Vậy $x=30°$

c) Tam giác IJK có: $\hat{I}+\hat{J}+\hat{K}=180°$ (tổng ba góc trong tam giác)

Do đó: $50°+x+x=180°$

$x+x=180°-50°$

$2x=130°$

$x=65°$

Vậy $x=65°$

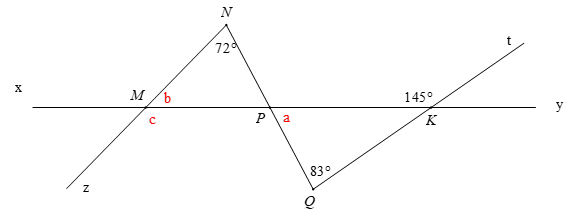
Bài 3. Tính số đo a; b; c trong các hình dưới đây:

Hướng dẫn giải

Ta có: $\widehat{PKt}=\widehat{PQK}+\widehat{QPK}$ (góc ngoài của tam giác)

Do đó: $145°=83°+a$

$a=145°-83°=62°$

Ta có: $\widehat{MPN}=\widehat{QPK}$ (hai góc đối đỉnh)

Do đó: $\widehat{MPN}=a=62°$

Có: $\widehat{NMP}+\widehat{MPN}+\widehat{PNM}=180°$ (tổng ba góc trong tam giác)

Do đó: $b+62°+72°=180°$

$b=180°-62°-72°=46°$

Có: $\widehat{zMP}+\widehat{NMP}=180°$ (hai góc kề bù)

Do đó: $c+b=180°$

$c+46°=180°$

$c=180°-46°=134°$

Vậy $a=62°$; $b=46°$; $c=134°$.