Lý thuyết Quan hệ giữa góc và cạnh đối diện trong một tam giác (Kết nối tri thức 2024) Toán 7
Tóm tắt lý thuyết Toán 7 Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác ngắn gọn, chính xác sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 7.
Lý thuyết Toán lớp 7 Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Lý thuyết Quan hệ giữa góc và cạnh đối diện trong một tam giác
1. Góc đối diện với cạnh lớn hơn trong một tam giác
Định lí 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
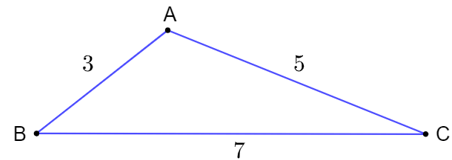
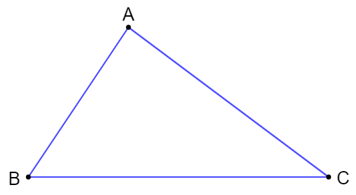
Ví dụ:Cho tam giác ABC có độ dài các cạnh: AB = 3 cm, BC = 5 cm, CA = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác ABC theo thứ tự từ bé đến lớn.
Hướng dẫn giải
Góc đối diện của cạnh AB là ˆC , góc đối diện của cạnh AC là ˆB và góc đối diện của cạnh BC là ˆA .
Trong tam giác ABC, vì AB = 3 cm, AC = 5 cm nên AB < AC. Do đó theo định lí 1 ta có: ˆC<ˆB (1).
Tương tự ta có do AC < BC (5 cm < 7 cm) nên theo định lí 1 ta có: ˆB<ˆA (2).
Từ (1) và (2) suy ra ˆC<ˆB<ˆA.
2. Cạnh đối diện với góc lớn hơn tỏng một tam giác
Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
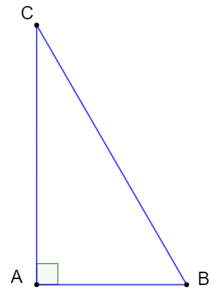
Ví dụ: Cho tam giác ABC vuông tại A có ˆB=60° . Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ lớn đến bé.
Hướng dẫn giải
Tam giác ABC cạnh đối diện của các góc ˆA,ˆB,ˆC lần lượt là BC, AC, AB.
Xét tam giác ABC vuông tại A, vì tổng số đo các góc trong một tam giác bằng , nên ta có: ˆA+ˆB+ˆC=180°.
Suy ra ˆC=180°−ˆA−ˆB .
Do đó ˆC=180°−90°−60°=30° .
Từ đó trong tam giác ABC, ta có: ˆA>ˆB>ˆC .
Theo định lí 2, ta suy ra BC > AC > AB.
Nhận xét
+ Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh đối diện với vuông góc (tức là cạnh huyền) là cạnh lớn nhất.
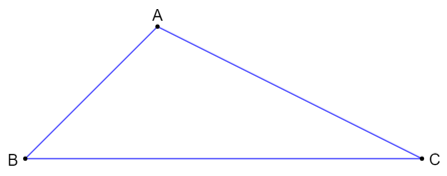
Ví dụ:Trong tam giác ABC vuông tại A, cạnh đối diện với góc vuông là BC nên BC là cạnh lớn nhất.
+ Tương tự trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.
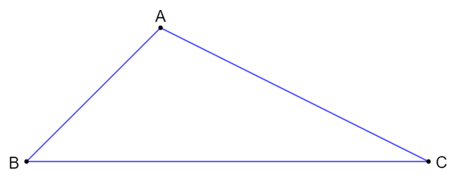
Ví dụ:Trong tam giác ABC là tam giác tù tại đỉnh A, có cạnh đối diện của góc tù là cạnh BC nên ở đây BC chính là cạnh lớn nhất.
Bài tập Quan hệ giữa góc và cạnh đối diện trong một tam giác
Bài 1: Hãy giải thích tại sao trong tam giác tù, cạnh đối diện góc tù là cạnh lớn nhất.
Hướng dẫn giải
Giả sử tam giác ABC là tam giác tù tại đỉnh A nên suy ra 90°<ˆA<180°(1)
Lại có tam giác ABC có tổng ba góc trong tam giác bằng 180º nên suy ra:
ˆA+ˆB+ˆC=180°
Do đó ˆA=180°−(ˆB+ˆC).
Do đó với 90°<180°−(ˆB+ˆC)<180°thì 0°<ˆB+ˆC<90°.
Hay ta suy ra được 0°<ˆB<90° và 0°<ˆC<90° (2)
Từ (1) và (2) ta có: ˆA>ˆB,ˆA>ˆC.
Theo định lí 2, ta có: BC > AC và BC > AB nên BC là cạnh lớn nhất.
Vậy trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất (đpcm).
Bài 2: Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60º.
Hướng dẫn giải
Xét tam giác ABC có BC là cạnh lớn nhất và góc đối diện của cạnh BC là ˆA .
Theo định lí 1, ta có ˆA là góc lớn nhất thỏa mãn: ˆA≥ˆB,ˆA≥ˆC .
Suy ra ˆA+ˆA+ˆA≥ˆA+ˆB+ˆC
Hay 3ˆA≥ˆA+ˆB+ˆC
Do đó ˆA≥ˆA+ˆB+ˆC3=180°3=60° .
Vậy suy ra số đo góc A lớn hơn hoặc bằng 60º (đpcm).
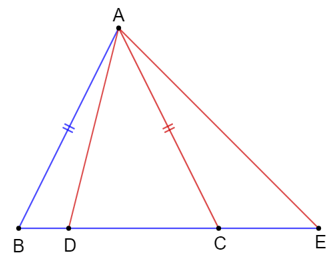
Bài 3: Cho tam giác ABC cân tại A, hai điểm D, E nằm trên đường thẳng BC, D nằm giữa B và C, C nằm giữa D và E. Hãy chứng minh AD < AC < AE.
Hướng dẫn giải
Do trong một tam giác cân, hai góc của đáy luôn bé hơn 90º nên suy ra ^ACB là góc nhọn.
Mà ^ACE kề bù với ^ACB nên suy ra ^ACE là góc tù.
Xét tam giác ACE có ^ACE là góc tù nên cạnh đối diện với ^ACE là cạnh AE là cạnh lớn nhất.
Suy ra AE > AC (*)
Mà tam giác ABC cân tại A nên AB = AC và ^ABC=^ACB.
Lại có:
∙ Xét tam giác ABC có: ^BAC+^ABC+^ACB=180°
Suy ra ^BAC=180°−2^ABC(1)
∙ Xét tam giác ABD có: ^BAD+^ABD+^ADB=180°
Suy ra ^BAD=180°−^ABD−^ADB(2)
Mà D nằm giữa B và C nên suy ra ^BAD<^BAC(3)
Từ (1), (2) và (3) ta suy ra được:
180°−^ABD−^ADB<180°−2^ABC
Hay ^ABC+^ADB>2^ABC.
Do đó ^ADB>^ABC.
Áp dụng định lí 2 ta được: AB > AD.
Mà AB = AC (cmt) nên suy ra AC > AD (**)
Từ (*) và (**) nên suy ra AE > AC > AD (đpcm).