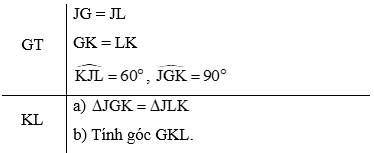Lý thuyết Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác (Kết nối tri thức 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Lý thuyết Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

1. Hai tam giác bằng nhau

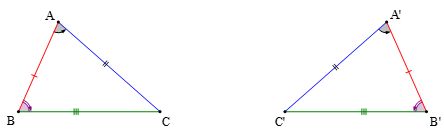
• Hai tam giác ABC và A'B'C'bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, nghĩa là:

AB=A'B'; AC=A'C'; BC=B'C' và $\hat{A}=\widehat{A\text{'}}$; $\hat{B}=\widehat{B\text{'}}$; $\hat{C}=\widehat{C\text{'}}$.

• Khi kí hiệu hai tam giác bằng nhau thì thứ tự các đỉnh tương ứng phải được viết theo cùng 1 thứ tự.

Ở đây hai đỉnh A và A' (B và B', C và C') là hai đỉnh tương ứng;

Hai góc A và A' (B và B', C và C') là hai góc tương ứng;

Hai cạnh AB và A'B' (AC và A'C', BC và B'C') là hai cạnh tương ứng.

Khi đó ta kí hiệu: $\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$

Ví dụ:

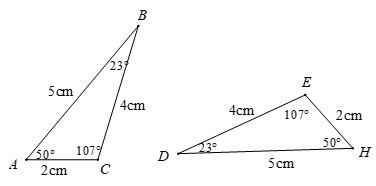
+ Cho hai tam giác trong hình dưới đây, ta thấy:

$\hat{A}=\hat{H}=50°$; $\hat{B}=\hat{D}=23°$; $\hat{C}=\hat{E}=107°$(các góc tương ứng)

AB = DH = 5 cm; BC = DE = 4cm; AC = EH = 2cm (các cạnh tương ứng)

Do đó hai tam giác trên bằng nhau. Kí hiệu theo thứ tự tương ứng là: $\Delta ABC=\Delta HDE$

2. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh – cạnh – cạnh (c.c.c)

• Cách vẽ tam giác khi biết số đo ba cạnh.

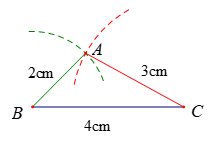
Chẳng hạn: Vẽ tam giác ABC biết AB = 2 cm; AC = 3 cm; BC = 4 cm.

+ Dùng thước kẻ có vạch chia vẽ đoạn BC = 4 cm (hoặc có thể vẽ AB hoặc AC trước)

+ Dùng compa mở khẩu độ 2 cm, tâm tại điểm B, vẽ 1 cung tròn; mở compa khẩu độ 3 cm, tâm tại điểm C, vẽ một cung tròn. Giao điểm của 2 cung tròn là điểm A.

+ Vẽ các đoạn thẳng AB; AC ta được tam giác ABC.

• Trường hợp bằng nhau cạnh - cạnh - cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ:

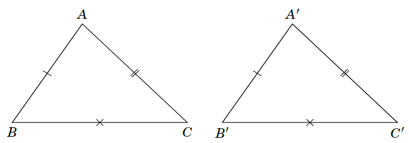
+ Cho tam giác ABC và tam giác $A\text{'}B\text{'}C\text{'}$ trong hình dưới đây:

Ta có: AB = $A\text{'}B\text{'}$; AC = A'C'; BC = B'C'

Khi đó: $\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$

Chú ý:

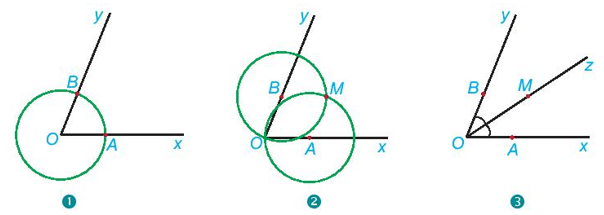
• Cách vẽ tia phân giác của một góc dựa và thước kẻ và compa.

Vẽ tia phân giác của góc xOy ta làm như sau:

1) Vẽ đường tròn tâm O cắt Ox, Oy lần lượt tại A và B.

2) Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn này cắt nhau tại điểm M khác điểm O.

3) Vẽ tia Oz đi qua M. Tia Oz là tia phân giác của góc xOy.

Bài tập Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

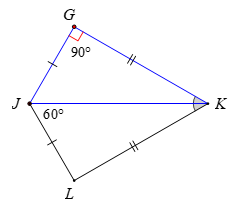
Bài 1. Cho hình vẽ dưới đây, biết JG = JL, GK = LK, $\widehat{KJL}=60°$, $\widehat{JGK}=90°$.

a) Chứng minh rằng $\Delta JGK=\Delta JLK$

b) Tính góc GKL.

Hướng dẫn giải

a) Xét hai tam giác JGK và JLK có:

JG = JL (theo giả thiết)

GK = LK (theo giả thiết)

JK là cạnh chung

Vậy $\Delta JGK=\Delta JLK$(c.c.c)

b) Vì $\Delta JGK=\Delta JLK$(theo câu a)

⇒ $\widehat{KJG}=\widehat{KJL}$(hai góc tương ứng)

⇒ $\widehat{KJG}=60°$

Xét tam giác JGK có: $\widehat{KJG}+\widehat{JGK}+\widehat{GKJ}=180°$(tổng 3 góc trong tam giác)

⇒ $60°+90°+\widehat{GKJ}=180°$

⇒ $\widehat{GKJ}=180°-60°-90°=30°$

Vì $\Delta JGK=\Delta JLK$(theo câu a)

⇒ $\widehat{GKJ}=\widehat{LKJ}$(hai góc tương ứng)

⇒ $\widehat{GKL}=\widehat{GKJ}+\widehat{LKJ}=\widehat{GKJ}+\widehat{GKJ}=2\widehat{GKJ}=2\cdot 30°=60°$

Vậy $\widehat{GKL}=60°$

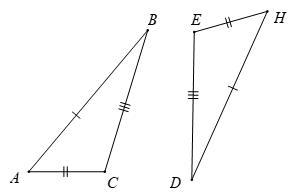
Bài 2. Cho tam giác ABC và DEH trong hình dưới đây.

Xác định trong các khẳng định sau, khẳng định nào đúng?

a) $\Delta ABC=\Delta DEH$;

b) $\Delta ABC=\Delta HDE$;

c) $\Delta BAC=\Delta DEH$;

d) $\Delta BCA=\Delta DEH$.

Hướng dẫn giải

Hai tam giác ABC và HDE có:

AB = HD

BC = DE

AC = HE

Vậy $\Delta ABC=\Delta HDE$(c.c.c)

Khi đó A và H (B và D; C và E) là hai đỉnh tương ứng

a) $\Delta ABC=\Delta DEH$

Các đỉnh tương ứng không viết cùng thứ tự nên khẳng định sai.

b) $\Delta ABC=\Delta HDE$

Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.

c) $\Delta BAC=\Delta DEH$

Đỉnh A và H; đỉnh C và E không được viết cùng thứ tự nên khẳng định sai.

d) $\Delta BCA=\Delta DEH$

Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.

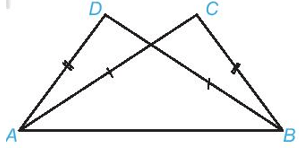
Bài 3. Cho hình vẽ dưới đây, biết AD = BC, AC = BD. Chứng minh rằng $\Delta ADB=\Delta BCA$.

Hướng dẫn giải

Hai tam giác ADB và BCA có:

AD = BC (theo giả thiết)

BD = AC (theo giả thiết)

AB là cạnh chung

Vậy $\Delta ADB=\Delta BCA$(c.c.c)