Vận dụng trang 45 Toán 10 Tập 2:
Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H.7.14) để người bơi có thể ngồi dựa lưng vào thành các bể sục thư giãn. Hãy tìm bán kính của các bể sục để tổng chu vi của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy π ≈ 3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai
Giải Toán 10 (Kết nối tri thức) Bài 21: Đường tròn trong mặt phẳng tọa độ
Luyện tập 2 trang 44 Toán 10 Tập 2:
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng,
a) x2 – y2 – 2x + 4y – 1 = 0
b) x2 + y2 – 2x + 4y + 6 = 0
c) x2 + y2 + 6x – 4y + 2 = 0
Giải Toán 10 (Kết nối tri thức) Bài 21: Đường tròn trong mặt phẳng tọa độ
Giải bài tập Toán 10 Bài 21: Đường tròn trong mặt phẳng tọa độ
A. Câu hỏi
Giải Toán 10 trang 43 Tập 2
Hoạt động 1 trang 43 Toán 10 Tập 2:
Trong mặt phẳng toạ độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R (H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi toạ độ của nó thoả mãn điều kiện đại số nào?
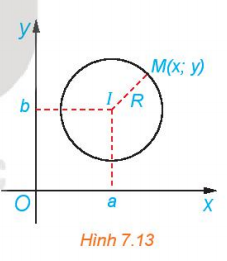
Giải Toán 10 (Kết nối tri thức) Bài 21: Đường tròn trong mặt phẳng tọa độ
Bài 7.12 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại 3 vị trí O(0; 0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh.
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Giải Toán 10 trang 42 Tập 2
Bài 7.9 trang 42 Toán 10 Tập 2:
Trong mặt phẳng toạ độ Oxy cho điểm A(0; –2) và đường thẳng ∆ : x + y – 4 = 0
a) Tính khoảng cách từ điểm A đến đường thẳng ∆.
b) Viết phương trình đường thẳng a đi qua điểm M(–1; 0) và song song với ∆.
c) Viết phương trình đường thẳng b đi qua điểm N(0; 3) và vuông góc với ∆.
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
B. Bài tập
Bài 7.7 trang 41 Toán 10 Tập 2:
Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) ∆1 : 3x + y –= 0 và ∆2 : 6x + 2y –= 0
b) d1 : x –y + 2 = 0 và d2 : x – 3y + 2 = 0
c) m1 : x – 2y + 1= 0 và m2 : 3x + y – 2 = 0
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Giải Toán 10 trang 41 Tập 2
Vận dụng trang 41 Toán 10 Tập 2:
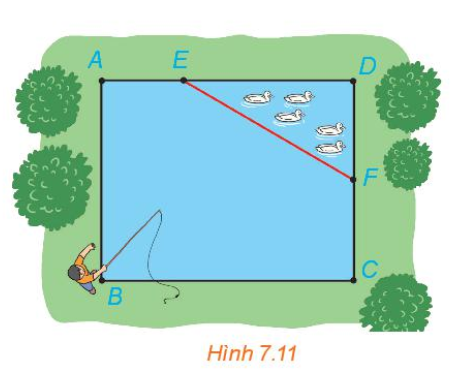
Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15m, chiều rộng AB = 12m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5m, CF = 6m (H.7.11)
a) Chọn hệ trục toạ độ Oxy, có điểm O trùng với điểm B, các tia Ox, Oy tương ứng trùng với các tia BC, BA. Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng 1m trong thực tế. Hãy xác định toạ độ của các điểm A, B, C, D, E, F và viết phương trình đường thẳng EF.
b) Nam đứng ở vị trí B câu cá có thể quăng lưỡi câu xa 10,7 m . Hỏi lưỡi câu có thể rơi vào ao nuôi vịt hay không ?
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Trải nghiệm trang 40 Toán 10 Tập 2:
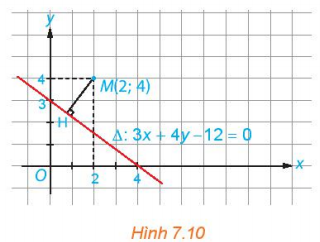
Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4.
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Giải Toán 10 trang 40 Tập 2
Hoạt động 4 trang 40 Toán 10 Tập 2:
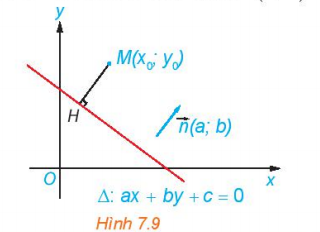
Cho điểm M(x0; y0) và đường thẳng ∆ : ax + by + c = 0 có vectơ pháp tuyến (a; b). Gọi H là hình chiếu vuông góc của M lên ∆ (H.7.9).
a) Chứng minh rằng
b) Gỉa sử H có toạ độ (x1; y1). Chứng minh rằng:
c) Chứng minh rằng HM =
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
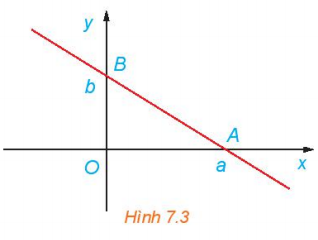
Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0.
a) Chứng minh rằng ∆ cắt trục hoành.
b) Lập phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆.
c) Hãy chỉ ra mối quan hệ giữa và
d) Gọi M là giao điểm của ∆0 với nửa đường tròn đơn vị và x0 là hoành độ của M. Tính tung độ của M theo x0 và a. Từ đó, chứng minh tan= a
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Giải Toán 10 trang 38 Tập 2
Hoạt động 3 trang 38 Toán 10 Tập 2:
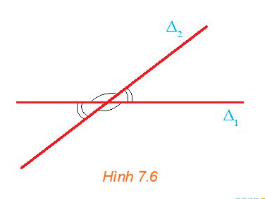
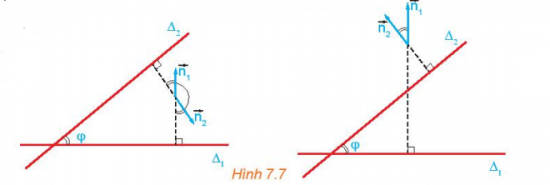
Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến . Gọi φ là góc giữa hai đường thẳng đó (H7.7). Nêu mối quan hệ giữa:
a) góc φ và góc ();
b) cos φ và cos().
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Giải Toán 10 trang 37 Tập 2
Luyện tập 1 trang 37 Toán 10 Tập 2:
Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) ∆1: x + 4y – 3 = 0 và ∆2: x – 4y – 3 = 0;
b) ∆1: x + 2y – = 0 và ∆2: 2x + 4y – 3 = 0.
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Giải bài tập Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
A. Câu hỏi
Giải Toán 10 trang 36 Tập 2
Hoạt động 1 trang 36 Toán 10 Tập 2:
Trong mặt phẳng toạ độ, cho hai đường thẳng
∆1: x – 2y + 3 = 0
∆2: 3x – y – 1 = 0
a) Điểm M(1; 2) có thuộc hai đường thẳng nói trên hay không?
b) Giải hệ ![]()
c) Chỉ ra mối quan hệ giữa toạ độ giao điểm của ∆1 và ∆2 với nghiệm của hệ phương trình trên.
Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
Bài 7.6 trang 34 Toán 10 Tập 2: Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2º Bắc, kinh độ 105,8º Đông, sân bay Đà Nẵng có vĩ độ 16,1º Bắc, kinh độ 108,2º Đông. Một máy bay bay từ sân bay Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ xº Bắc , kinh độ yº Đông được tính theo công thức:
a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?
b) Tại thời điểm 1 giờ kể từ lúc cất cánh máy bay đã bay qua vĩ tuyến 17 (17º Bắc) chưa?
Giải Toán 10 (Kết nối tri thức) Bài 19: Phương trình đường thẳng
B. Bài tập
Bài 7.1 trang 34 Toán 10 Tập 2:
Trong mặt phẳng toạ độ, cho = (2; 1) , = (3; 2), A(1; 3), B(-2; 1).
a) Lập phương trình tổng quát của đường thẳng ∆1 đi qua A và có vectơ pháp tuyến .
b) Lập phương trình tham số của đường thẳng ∆2 đi qua B và có vectơ chỉ phương .
c) Lập phương trình tham số của đường thẳng AB.
Giải Toán 10 (Kết nối tri thức) Bài 19: Phương trình đường thẳng
Giải Toán 10 trang 34 Tập 2
Vận dụng trang 34 Toán 10 Tập 2:
Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1686 – 1736) được xác định bởi hai mốc sau:
Nước đóng băng ở 0ºC; 32ºF
Nước sôi ở 100ºC; 212ºF
Trong quy đổi đó, nếu aºC tương ứng với bºF thì trên mặt phẳng toạ độ Oxy, điểm M(a; b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212). Hỏi 0ºF, 100ºF tương ứng với bao nhiêu độ C?
Giải Toán 10 (Kết nối tri thức) Bài 19: Phương trình đường thẳng
Hoạt động 4 trang 33 Toán 10 Tập 2:
Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vận tốc (3; 4).
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và vectơ chỉ phương của đường thẳng đó).
b) Chứng minh rằng tại thời điểm t (t > 0) tính từ khi khởi hành, vật thể ở vị trí có toạ độ là (2 + 3t; 1 + 4t).
Giải Toán 10 (Kết nối tri thức) Bài 19: Phương trình đường thẳng
Bài 6.34 trang 29 Toán 10 Tập 2: Một công ty bắt đầu sản xuất và bán một loại máy tính xách tay từ năm 2018. Số lượng loại máy tính đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 3,2 nghìn và 4 nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ năm 2018, số lượng máy tính loại đó bán được mỗi năm có thể được mô tả bởi một hàm số bậc hai.
Giả sử t là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại máy tính đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm (0; 3,2) và (1; 4). Giả sử điểm (0; 3,2) là đỉnh đồ thị của hàm số bậc hai này.
a) Lập công thức của hàm số mô tả số lượng máy tính xách tay bán được qua từng năm.
b) Tính số lượng máy tính xách tay đó bán được trong năm 2024.
c) Đến năm bao nhiêu thì số lượng máy tính xách tay đó bán được trong năm sẽ vượt mức 52 nghìn chiếc?
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 6