Lý thuyết Bài toán thời gian – quãng đường
Lý thuyết Bài toán thời gian – quãng đường
Bài toán 1. Tìm khoảng thời gian ngắn nhất vật đi từ x1 đến x2
A. Lí thuyết và phương pháp giải
|
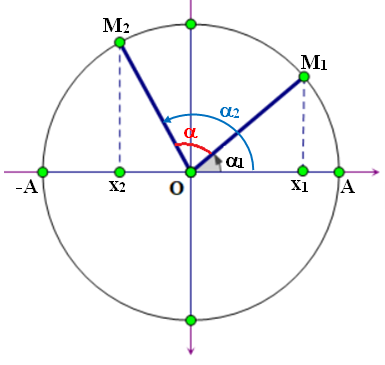
- Dựa vào tính chất dđđh là hình chiếu của chuyển động tròn đều trên một đường thẳng. - Khi ở vị trí x1, x2: cosα1=x1A⇒α1=arccosx1Acosα2=x2A⇒α2=arccosx2A}⇒α=|α1−α2| |
|
Khoảng thời gian ngắn nhất vật đi từ vị trí x1 sang vị trí x2: t=αω=α2πT
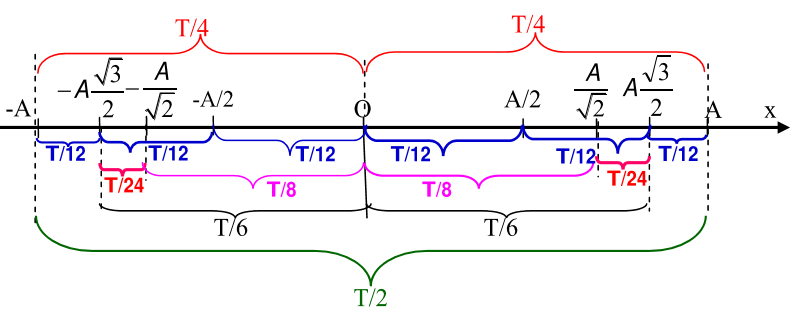
Cách tìm thời gian và quãng đường nhanh bằng trục thời gian:
B. Ví dụ minh hoạ
Ví dụ: Một vật dao động điều hòa dọc theo trục Ox với phương trình x=10cos(4π3t−2π3)cm. Tìm khoảng thời gian ngắn nhất để vật di chuyển trong từng trường hợp sau:
a. Từ vị trí cân bằng đến điểm có li độ x = 5cm.
b. Từ vị trí biên dương đến điểm có li độ x=5√3cm.
c. Từ vị trí có li độ x=−5√2cm đến điểm có li độ x = 5cm.
d. Từ điểm có li độ x=−5cm đến điểm có li độ x=−5√3cm.
Hướng dẫn giải
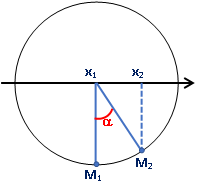
Cách 1: dựa vào vòng tròn lượng giác
a. Khi vật đi từ vị trí cân bằng (x = 0) đến điểm có li độ
Þ Thời gian: t=αω=π/64π/3=0,125
b. Khi vật đi từ vị trí biên dương đến điểm có li độ (sẽ đi theo chiều âm nên lấy góc dương)
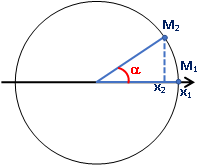
Þ Thời gian:
c. Khi vật đi từ vị trí có li độ ® đến điểm có li độ (sẽ đi theo chiều dương nên lấy góc âm)
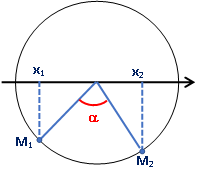
Þ Thời gian:
d. Khi vật đi từ vị trí có li độ ® đến điểm có li độ (sẽ đi theo chiều âm nên lấy góc dương)
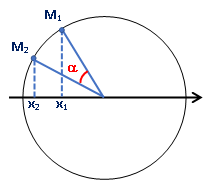
Þ Thời gian:
Cách 2: Sử dụng trục thời gian
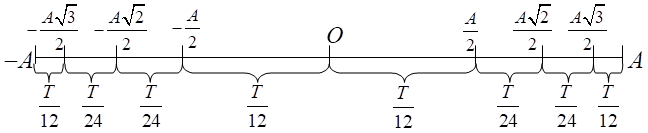
Từ phương trình dao động, ta có:
a. Thời gian vật đi từ vị trí cân bằng (x = 0) đến điểm có li độ
b. Thời gian vật đi từ vị trí biên dương (x = A) đến điểm có li độ là
c. Thời gian vật đi từ vị trí có li độ đến điểm có li độ là
d. Thời gian vật đi từ điểm có li độ đến điểm có li độ là
Bài toán 2. Tìm quãng đường dựa vào khoảng thời gian đã cho
A. Lí thuyết và phương pháp giải
* Khi thời gian t có: , n: nguyên hoặc bán nguyên
* Quãng đường khi t bất kì:
Phân tích t = n.T + Dt Þ S = 4A.n + DS (n: nguyên)
Tìm DS dựa vào thời điểm ban đầu t = 0: và thời điểm cuối cùng t: Þ DS
* Tốc độ trung bình:
* Vận tốc trung bình:
B. Ví dụ minh hoạ
Ví dụ 1. Một chất điểm dao động điều hoà theo phương trình . Tính quãng đường vật đi được trong khoảng thời gian từ t = 1 s đến t = 2,5 s.
Hướng dẫn giải
Từ phương trình dao động, ta có:
Khoảng thời gian: (là số bán nguyên)
Þ Quãng đường vật đi được:
Ví dụ 2: Một vật dao động điều hòa dọc theo trục Ox với phương trình (cm). Từ thời điểm ban đầu đến thời điểm , quãng đường vật đi được là bao nhiêu?
Hướng dẫn giải
Ta có: . Mặt khác
Do đó:
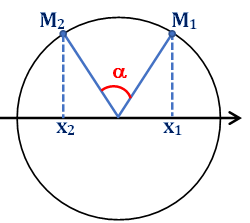
Cách 1: Xác định Ds dựa vào vòng tròn:
Tại thời điểm ban đầu
Trong thời gian , góc quét trên vòng tròn:
® Quét trên vòng tròn, ta thấy vật đến vị trí có li độ .
Do đó: s = 28.4 + 4 = 116 cm .
Cách 2: Xác định Ds dựa vào trục thời gian
Tại thời điểm ban đầu .

Trong thời gian vật đi từ vị trí có li độ .
Do đó: s = 28.4 + 4 = 116 cm .