Lý thuyết Xác định các đại lượng dựa vào công thức
Lý thuyết Xác định các đại lượng dựa vào công thức
A. Lí thuyết và phương pháp giải
+ Các công thức độc lập thời gian:
A2=x2+(vω)2=a2ω4+v2ω2 hay (xA)2+(vvmax)2=(aamax)2+(vvmax)2=1
Đề cho li độ và vận tốc tại hai thời điểm khác nhau x1, x2 và v1, v2, yêu cầu tính w:
|
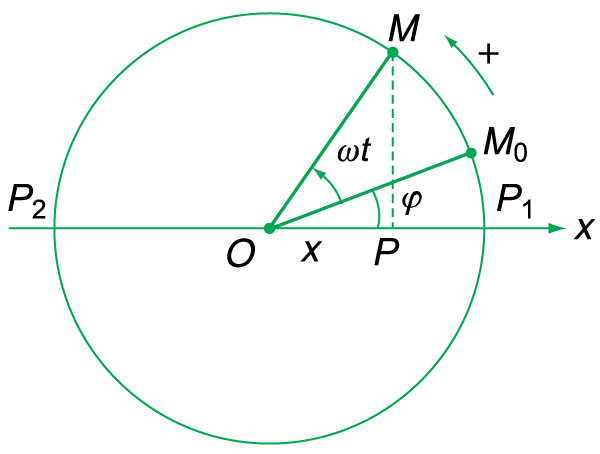
+ Mối liên hệ giữa dao động điều hòa và chuyển động tròn đều: Điểm M chuyển động tròn đều với tốc độ góc ω. Gọi P là hình chiếu của M trên trục Ox. Điểm P dao động điều hòa với phương trình. x=OMcos(ωt+φ) |
|
B. Ví dụ minh hoạ
Ví dụ 1. Một vật dao động điều hoà với tần số 60,0 Hz và biên độ 2,50 cm. Tính tốc độ của vật khi nó ở li độ 0,800 cm.
Hướng dẫn giải
Tần số góc: f=ω2π⇒ω=2πf=2π.60=120π( rad/s)
Áp dụng công thức: v=±ω√A2−x2=±893 .
Ví dụ 2. Một dao động điều hoà trên đoạn thẳng dài và thực hiện được 50 dao động trong thời gian . Tìm vận tốc và gia tốc của vật khi đi qua vị trí có li độ theo chiều hướng về vị trí cân bằng?
Hướng dẫn giải
.
Khi thì gia tốc .
Vì vật có li độ âm, đang hướng về vị trí cân bằng nên . Vậy .