Lý thuyết Xác định các đại lượng đặc trưng của sóng cơ

A. Lí thuyết và phương pháp giải

- Chu kì (T), vận tốc (v), tần số (f), bước sóng (λ) liên hệ với nhau:

f = $\frac{1}{\text{T}}$ ; λ = v.T = $\frac{\text{v}}{\text{f}}$ ; v = $\frac{\mathrm{\Delta s}}{\mathrm{\Delta t}}$ với Δs là quãng đường sóng truyền trong thời gian Δt

- Quan sát hình ảnh sóng có n ngọn sóng liên tiếp thì có n - 1 bước sóng.

- Số lần nhô lên trên mặt nước là N trong khoảng thời gian t giây thì chu kì T = $\frac{\text{t}}{\text{N }-1}$

B. Ví dụ minh hoạ

Ví dụ 1: Hình dưới là hình ảnh của một sóng trên dây đàn hồi tại một thời điểm xác định. Cho biết thời gian A ngắn nhất để điểm A từ vị trí cân bằng dao động theo phương thẳng đứng và trở lại vị trí này là 0,25 s và khoảng cách AB bằng 40 cm.

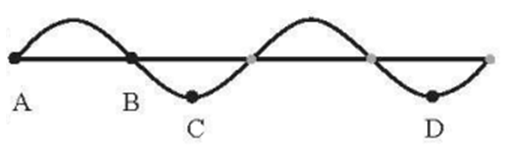
a) Tính tốc độ truyền sóng trên dây.

b) Khoảng cách CD bằng bao nhiêu?

Hướng dẫn giải

a) Ta có: $\frac{\mathrm{T}}{2}=0,25\text{ s}$ và $\frac{\mathrm{\lambda }}{2}=40\text{ cm}$. Kết hợp với công thức $\mathrm{\lambda }=\mathrm{vT}$

$\Rightarrow \mathrm{v}=\frac{40.2}{0,25.2}=160\text{ cm/s}$.

b) $\text{CD}=\mathrm{\lambda }=80\text{ cm}$.

Ví dụ 2: Một sóng cơ lan truyền với tần số ƒ = 500 Hz, biên độ A = 0,25 mm. Sóng lan truyền với bước sóng  λ = 70 cm.

a. Tính tốc độ truyền sóng.

b. Tính tốc độ dao động cực đại của các phần tử vật chất môi trường.

Hướng dẫn giải

a. Ta có $\mathrm{\lambda }=\frac{\mathrm{v}}{\mathrm{f}}$  Þ v = λƒ = 0,7.500 = 350 m/s.

b. Tốc độ cực đại của phần tử môi trường : v_max = ω.A = 2πƒ.A = 2π.500.0,25.10^-3 = 0,25π = 0,785 m/s.

Ví dụ 3: Hình dưới là đồ thị (u - t) của một sóng âm trên màn hình của một dao động kí. Biết mỗi cạnh của ô vuông theo phương ngang trên hình tương ứng vói 1 ms. Tính tần số của sóng.

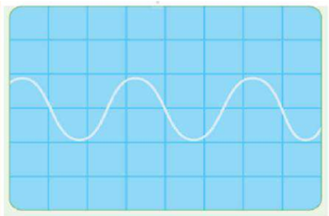
Hướng dẫn giải

- Từ đồ thị ta thấy 1 chu kì sóng tương ứng với 3 ô vuông. Suy ra T = 3 ms

- Tần số $\mathrm{f}=\frac{1}{\mathrm{T}}=\frac{1}{3{.10}^{-3}}=\frac{1000}{3}\text{ Hz.}$

Ví dụ 4: Một sóng cơ học có tần số 45 Hz lan truyền với tốc độ 360 cm/s. Tính

a. khoảng cách gần nhất giữa hai điểm trên phương truyền sóng dao động cùng pha.

b. khoảng cách gần nhất giữa hai điểm trên phương truyền sóng dao động ngược pha.

c. khoảng cách gần nhất giữa hai điểm trên phương truyền sóng dao động vuông pha.

Hướng dẫn giải

Từ giả thiết ta tính được bước sóng λ = v/ƒ = 360/45 = 8 cm.

a. Khoảng cách gần nhất giữa hai điểm dao động cùng pha là d_min = λ = 8 cm.

b. Khoảng cách gần nhất giữa hai điểm dao động ngược pha là d_min = λ/2 = 4 cm.

c. Khoảng cách gần nhất giữa hai điểm dao động vuông pha là d_min = λ/4 = 2 cm.

Ví dụ 5: Một người quan sát sóng trên mặt hồ thấy khoảng cách giữa hai ngọn sóng liên tiếp bằng 2 m và có 6 ngọn sóng truyền qua trước mặt trong 8 s.

a. Tính bước sóng.

b. Tìm chu kì dao động.

c. Tính tốc độ truyền sóng.

Hướng dẫn giải

a. Khoảng cách giữa 2 ngọn sóng liên tiếp là λ nên ta có λ = 2 m.

6 ngọn sóng truyền qua tức là sóng đã thực hiện được 5 chu kỳ dao động,

Khi đó 5T = 8  Þ T = 1,6 s.

c. Tốc độ truyển sóng là v = λ/T = 1,25 m/s