Lý thuyết Các bài toán liên quan đến tính chất của hình lăng trụ và hình hộp

- Hình lăng trụ có hai mặt đáy là hai đa giác lồi nằm trên hai mặt phẳng song song và các cạnh bên là các đường thẳng song song.

- Hình lăng trụ có hai đáy là hình bình hành được gọi là hình hộp.

- Các tính chất của hình lăng trụ:

+ Hai mặt đáy của hình lăng trụ song song với nhau.

+ Các cạnh bên của hình lăng trụ song song với nhau.

+ Các mặt bên của hình lăng trụ là hình bình hành.

- Các tính chất của hình hộp:

+ Các mặt đối diện của hình hộp song song với nhau.

+ Các mặt của hình hộp đều là hình bình hành.

+ Các đường chéo của hình hộp cắt nhau tại trung điểm của mỗi đường.

Ví dụ 1. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Mặt phẳng (P) song song với mặt đáy của hình lăng trụ và cắt các cạnh bên của hình lăng trụ tại M, N, P, Q. Chứng mình rằng ABCD.MNPQ là hình lăng trụ.

Hướng dẫn giải:

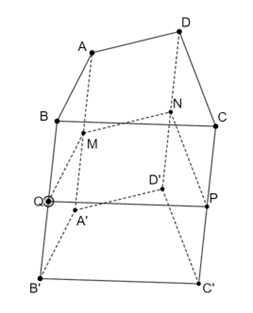
Vì M, N, P, Q nằm trên các cạnh bên của hình lăng trụ, mà các cạnh bên của các hình lăng trụ song song với nhau nên AM // BN // CP // DQ.

Hơn nữa (ABCD) và (MNPQ) song song với nhau nên ABCD.MNPQ là hình lăng trụ tứ giác.

Ví dụ 2. Cho hình hộp ABCD.MNPQ. Chứng minh rằng các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.

Hướng dẫn giải:

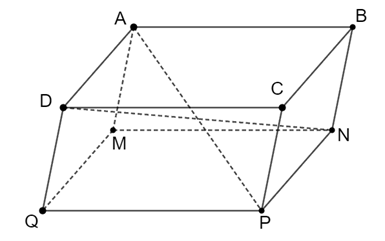
Vì đáy của hình hộp là hình bình hành nên AD // BC và AD = BC.

Mặt bên BCPN là hình bình hành nên BC // NP và BC = NP.

Suy ra AD // NP và AD = NP, từ đó ta được ADPN là hình bình hành.

Vậy AP và ND cắt nhau tại trung điểm mỗi đường.

Tương tự ta được BQ và AP cắt nhau tại trung điểm mỗi đường.

Vậy các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.