Lý thuyết Xác định, chứng minh hai mặt phẳng song song

 Để chứng minh hai mặt phẳng song song:

+ Cách 1: Chứng minh rằng trong một mặt phẳng có hai đường thẳng cắt nhau và cùng song song với mặt phẳng còn lại.

+ Cách 2: Chứng minh hai mặt phẳng đó cùng song song với mặt phẳng thứ ba.

Ví dụ 1. Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC và SD. Chứng minh (MNPQ) // (ABCD).

Hướng dẫn giải:

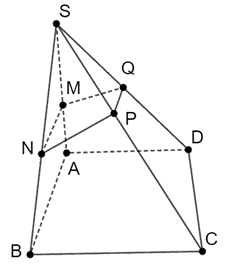
Do M và N lần lượt là trung điểm của SA và SB

⇒ MN là đường trung bình của tam giác SAB và MN // AB.

Mà AB ⊂ (ABCD) nên MN // (ABCD)   (1)

Do M và P lần lượt là trung điểm của SA và SC

⇒ MP là đường trung bình của tam giác SAC và MP // AC.

Mà AC ⊂ (ABCD) nên MP // (ABCD)  (2)

Từ (1) và (2), kết hợp với MN và MP là hai đường thẳng cắt nhau tại M và cùng thuộc mp(MNPQ) ta suy ra: (ABCD) // (MNPQ).