Lý thuyết Chứng minh hai đường thẳng song song và các bài toán liên quan

 - Các tính chất của hai đường thẳng song song

+ Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.

+ Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

+ Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy hoặc đôi một cắt nhau.

+ Hệ quả: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

- Các cách để chứng minh hai đường thẳng song song:

+ Chứng minh hai đường thẳng đó cùng song song với đường thẳng thứ ba.

+ Chứng minh hai đường thẳng đó đồng phẳng, sau đó áp dụng các phương pháp chứng minh song song trong hình học phẳng (ví dụ tính chất đường trung bình, định lý Talet đảo, …).

+ Áp dụng định lý về giao tuyến song song.

+ Nếu hai mặt phẳng phân biệt lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Ví dụ 1. Trong mặt phẳng có 3 đường thẳng phân biệt a, b và c. Biết a và b cùng song song với c. Vậy a và b có bao nhiêu điểm chung?

Hướng dẫn giải:

Hai đường thẳng a và b cùng song song với c nên a và b có thể trùng nhau hoặc song song với nhau.

Mà a và b là hai đường thẳng phân biệt nên a và b không thể trùng nhau, a và b song song với nhau.

Vậy a và b không có điểm chung.

Ví dụ 2:

Cho hình tứ diện ABCD. M và N lần lượt là trọng tâm tam giác ACD và ABC. Xác định vị trí tương đối của MN và CD.

Hướng dẫn giải:

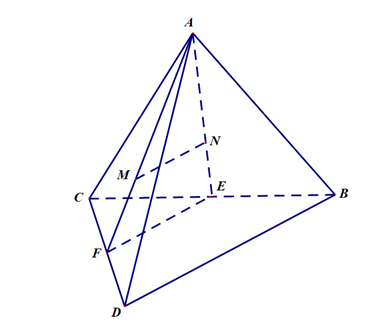
Gọi E và F lần lượt là trung điểm của BC và CD. EF là đường trung bình của tam giác BCD nên EF // CD        (1)

Do M và N lần lượt là trọng tâm các tam giác ACD và ABC nên $\frac{AM}{AF}=\frac{AN}{AE}=\frac{2}{3}$.

Suy ra MN // EF (định lí Thalès đảo) (2)

Từ (1) và (2) suy ra MN // CD.