Lý thuyết Xác định giao tuyến của hai mặt phẳng

- Nếu hai đường thẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó.

- Giao tuyến là đường thẳng chung của hai mặt phẳng, tức là giao tuyến là đường thẳng thuộc cả hai mặt phẳng.

- Khi tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung thuộc cả hai mặt phẳng. Đường thẳng đi qua hai điểm chung này chính là giao tuyến cần tìm.

- Điểm đầu tiên của giao tuyến thường là một điểm dễ nhận thấy vì nằm trên cả hai mặt phẳng đã cho.

- Điểm thứ hai của giao tuyến được xác định bằng cách xác định hai đường thẳng cùng đi qua điểm đó, nằm trên cùng một mặt phẳng thứ ba và không song song với hai mặt phẳng đã cho. Điểm thứ hai của giao tuyến là giao điểm của hai đường thẳng này.

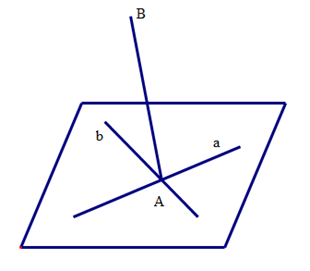
Ví dụ 1. Cho hai đường thẳng a và b cắt nhau tại điểm A. Điểm $B\notin \left(a,b\right)$. Xác định giao tuyến của (B, a) và (B, b).

Hướng dẫn giải:

Ta thấy $A\in a\Rightarrow A\in (B,a)$; $A\in b\Rightarrow A\in (B,b)$.

Vì vậy điểm $A\in \left(B,a\right)\cap \left(B,b\right)$.

Mà dễ thấy $B\in \left(B,a\right)\cap \left(B,b\right)$ nên $AB=\left(B,a\right)\cap \left(B,b\right)$.

Vậy AB là giao tuyến của (B, a) và (B, b).