Lý thuyết Xác định các quan hệ liên thuộc cơ bản giữa điểm, đường thẳng và mặt phẳng trong không gian

- Điểm A thuộc mặt phẳng (P), ký hiệu $A\in \left(P\right)$.

- Điểm B không thuộc mặt phẳng (P), ký hiệu $B\notin \left(P\right)$.

Nếu $A\in \left(P\right)$, ta còn nói A nằm trên (P), hoặc (P) chứa A, hoặc (P) đi qua A.

- Các cách xác định mặt phẳng:

+ Với 3 điểm A, B, C không thẳng hàng, có duy nhất một mặt phẳng (ABC) đi qua 3 điểm đó.

+ Với điểm $A\notin d$, có một và chỉ một mặt phẳng đi qua A và d. Ký hiệu (A, d).

+ Với hai đường thẳng a và b cắt nhau, có một và chỉ một mặt phẳng đi qua cả a và b. Ký hiệu (a, b).

Ví dụ 1. Cho tam giác ABC là điểm M thuộc đường thẳng AC. Điểm M và đường thẳng BM có thuộc mặt phẳng (ABC) không?

Hướng dẫn giải:

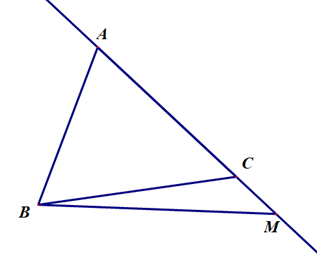
Vì hai điểm B và C nằm trên mặt phẳng (ABC) nên BC nằm trên mặt phẳng (ABC).

Điểm M thuộc đường thẳng BC nên M thuộc mặt phẳng (ABC).

A và M cùng nằm trên mặt phẳng (ABC) nên AM nằm trên mặt phẳng (ABC).