100 bài tập về bài toán thực tế hình không gian (2024 có đáp án) và cách giải các dạng toán

Các bài toán thực tế hình không gian và cách giải bài tập 

I. Các dạng bài tập

1. Dạng 1: Mặt cầu, hình cầu, khối cầu

Phương pháp giải: Nắm vững kiến thức các dạng toán để giải bài toán thực tế liên quan đến mặt cầu

Cho mặt cầu S (I; R)

- Diện tích mặt cầu: $S=4\pi R^2$

- Thể tích khối cầu: $V=\frac{4}{3}\pi R^3$

Ví dụ minh họa

Ví dụ 1: Một chậu nước hình bán cầu bằng nhôm có bán kính R = 10 đặt trong một khung hình hộp chữ nhật. Trong chậu chứa sẵn một khối nước hình chỏm cẩu có chiều cao h = 2. Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi. Cho biết công thức tính thể tích của khối chỏm cầu (O; R) có chiều cao h là $V_{c\mathrm{hom}}=\pi h^2\left(R-\frac{h}{3}\right)$ . Tính bán kính r của viên bi.

Lời giải

Ta có thể tích phần nước dâng lên chính bằng thể tích của viên bi bỏ vào

Do đó thể tích nước ban đầu $V_1=\pi h^2\left(R-\frac{h}{3}\right)$

Khi đó thể tích nước sau khi bỏ viên bi vào sẽ là:

$V_2=V_1+\frac{4}{3}\pi r^3$

$V_2=\pi h^2\left(R-\frac{h}{3}\right)+\frac{4}{3}\pi r^3$ (1)

Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi

Do vậy thể tích sau khi bỏ viên bi vào được tính bằng công thức:

$V_2=\pi {\left(2r\right)}^2\left(R-\frac{2r}{3}\right)$ (2)

Từ (1) và (2) ta có:

$$\begin{gathered} \pi h^2\left(R-\frac{h}{3}\right)+\frac{4}{3}\pi r^3 \\ =4\pi r^2\left(R-\frac{2r}{3}\right) \\ \iff 4r^3-4R{r}^2+h^2\left(R-\frac{h}{3}\right)=0 \end{gathered}$$

Thay R = 10; h = 2 ta được r = 9,905 hoặc r = 1,019

Vì bán kính của viên bi r = 9,905 xấp xỉ bằng chậu nước là điều vô lí

Ta chọn r = 1,019

Vậy bán kính của viên bi là r = 1,019.

Ví dụ 2: Quả bóng đá được dùng thi đấu tại các giải bóng đá Việt Nam tổ chức có chu vi của thiết diện qua tâm là 68,5cm. Quả bóng được ghép nối bởi các miếng da hình lục giác đều màu trắng và đen, mỗi miếng có diện tích $49,83c{m}^2$. Hỏi cần ít nhất bao nhiêu miếng da để làm quả bóng trên?

Lời giải

Giả sử bán kính mặt cầu là R

Ta có: $C=2\pi R$

$\Rightarrow R=\frac{68,5}{2\pi }=10,9cm$

Diện tích xung quanh mặt cầu:

$$\begin{gathered} S_{xq}=4\pi R^2 \\ {S}_{xq}=1493,6c{m}^2 \end{gathered}$$

Vậy số miếng da để làm quả bóng trên là: $N=\frac{S_{xq}}{S}$

$N=\frac{1493,6}{49,83}\approx 30$ (miếng)

Vậy cần ít nhất 30 miếng da để làm quả bóng trên.

2. Dạng 2: Mặt trụ, hình trụ, khối trụ

Phương pháp giải: Sử dụng công thức:

- Diện tích xung quanh hình trụ có bán kính R, chiều cao h là: $S_{xq}=2\pi Rh$

- Diện tích toàn phần hình trụ bằng tổng diện tích xung quanh hình trụ với diện tích hai đáy.

- Thể tích V của khối trụ tròn xoay có chiều cao h, bán kính mặt đáy R là: $V=\pi R^{2}h$

Ví dụ minh họa

Ví dụ 1: Người ta thiết kế một thùng chứa hình trụ có thể tích V nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỷ số $\frac{h}{r}$ sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?

Lời giải

Thể tích khối trụ là

$V=\pi r^{2}h\Rightarrow h=\frac{V}{\pi r^2}$

Giả sử số tiền làm mặt xung quanh là 1 thì số tiền mặt đáy và nắp là 3

Số tiền để làm thùng là $T=2\pi rh+6\pi r^2$

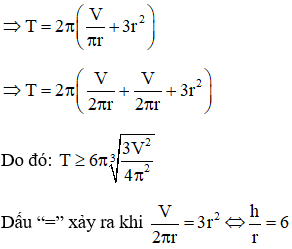
Ví dụ 2: Một cốc nước có dạng hình trụ chiều cao là 15 cm, đường kính đáy là 6 cm, lượng nước ban đầu trong cốc cao 10 cm. Thả vào cốc nước 5 viên bi thủy tinh hình cầu có cùng đường kính là 2 cm. Hỏi sau khi thả 5 viên bi, mực nước trong cốc cách miệng cốc bao nhiêu cm?

Lời giải

3. Dạng 3: Mặt nón, hình nón, khối nón

Phương pháp giải:

Sử dụng linh hoạt các công thức:

- Diện tích xung quanh: $S_{xq}=\pi rl$

- Diện tích đáy: $S_d=\pi r^2$

- Diện tích toàn phần: $S_{tp}=\pi rl+\pi r^2$

- Thể tích: $V=\frac{1}{3}{S}_d.h=\frac{1}{3}\pi r^{2}h$

Trong đó: h là chiều cao, l là đường sinh và r là bán kính đáy của hình nón.

Ví dụ minh họa

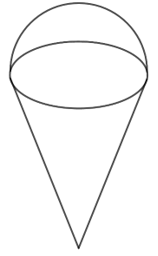
Ví dụ 1: Một chiếc kem gồm hai phần: phần phía dưới là khối nón có chiều cao gấp đôi bán kính đáy; phần phía trên là một nửa khối cầu có đường kính bằng đường kính khối nón bên dưới. Thể tích phần kem phía trên bằng $200c{m}^3$ . Tính thể tích của cả chiếc kem đã cho.

Lời giải

Thể tích phần kem phía trên bằng:

$\frac{2}{3}\pi r^3=200c{m}^3$

Thể tích phần kem phía dưới bằng:

$$\begin{gathered} \frac{\pi r^{2}h}{3}=\frac{\pi r^2\left(2r\right)}{3} \\ =\frac{2\pi r^3}{3}=200c{m}^3 \end{gathered}$$

Vậy thể tích của cả chiếc kem bằng $400c{m}^3$

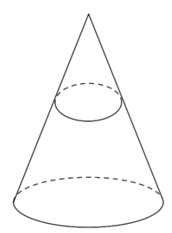
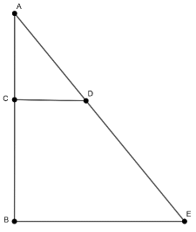
Ví dụ 2: Một vật $N_1$ có dạng hình nón có chiều cao bằng 40 cm. Người ta cắt vật $N_1$ bằng một mặt cắt song song với mặt đáy của nó để được một hình nón nhỏ $N_2$ có thể tích bằng $\frac{1}{8}$ thể tích $N_1$. Tính chiều cao h của hình nón $N_2$.

Lời giải

Gọi $r_1=BE,h_1=AB$ lần lượt là bán kính đáy và chiều cao của hình nón $N_1$

Gọi $r_2=CD,h=AC$ lần lượt là bán kính đáy và chiều cao của hình nón $N_2$

Khi đó thể tích hai khối nón lần lượt là:

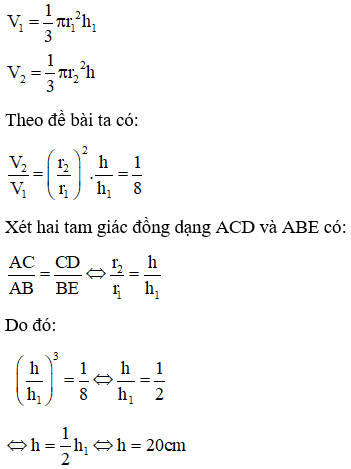
Vậy chiều cao của hình nón $N_2$ là h = 20 cm.

II. Bài tập áp dụng

Bài 1: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng $\frac{1}{3}$ chiều cao của phễu. Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên thì chiều cao của mực nước xấp xỉ bằng bao nhiêu. Biết rằng chiều cao của phễu là 15 cm.

A. 0,501 cm

B. 0,302 cm

C. 0,216 cm

D. 0, 188 cm

Bài 2: Cho một tấm bìa hình dạng tam giác vuông, biết b và c là độ dài cạnh tam giác vuông của tấm một khối tròn xoay. Hỏi thể tích V của khối tròn xoay sinh ra bởi tấm bìa bằng bao nhiêu?

A. $V=\frac{b^2{c}^2}{3\sqrt{b^2+c^2}}$

B. $V=\frac{\pi b^2{c}^2}{3\sqrt{b^2+c^2}}$

C. $V=\frac{2\pi b^2{c}^2}{3\sqrt{b^2+c^2}}$

D. $V=\frac{\pi b^2{c}^2}{3\sqrt{2(b^2+c^2)}}$

Bài 3: Một chiếc thùng chứa đầy nước có hình một khối lập phương. Đặt vào trong thùng đó một khối nón sao cho đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại trong thùng?

A. $\frac{\pi }{12-\pi }$

B. $\frac{\pi }{12}$

C. $\frac{1}{11}$

D. $\frac{11}{12}$

Bài 4: Một biệt thự có 10 cây cột nhà hình trụ tròn, tất cả có chiều cao 4,2 m. Trong đó 4 cây cột trước đại sảnh có đường kính 40 cm và 6 cây cột còn lại bên thân nhà có đường kính 26 cm. Chủ nhà dùng loại sơn giả đá để sơn 10 cây cột đó. Nếu giá của một loại sơn giả đá là 380.000 đồng $/m^2$ thì người chủ phải chi ít nhất bao nhiêu tiền để sơn 10 cây cột đó?

A. 14.647.000 đồng

B. 13.627.000 đồng

C. 16.459.000 đồng

D. 15.844.000 đồng

Bài 5: Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt là 1m và 1,5m. Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và thể tích bằng tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết quả nào?

A. 1,8 m

B. 2,1 m

C. 1,6 m

D. 2,5 m

Bài 6: Mặt tiền nhà văn hóa có 17 cây cột hình trụ tròn, tất cả có chiều cao 4,2 m. Trong đó 3 cây cột trước đại sảnh có đường kính 40 cm và 14 cây cột còn lại phân bố đều hai bên đại sảnh và chúng đều có đường kính 26 cm. Chủ đầu tư thuê nhân công để sơn các cây cột bằng loại sơn giả gỗ, biết giá thuê là $360.000/m^2$. Hỏi chủ đầu tư phải chi ít nhất bao nhiêu tiền để sơn hết các cây cột đó? $(\pi \approx 3,14159)$

A. 22 990 405 đồng

B. 5 473 906 đồng

C. 5 473 907 đồng

D. 22 990 407 đồng

Bài 7: Một bình nước dạng hình nón không có đáy đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích tràn ra ngoài là $18\pi \left(d{m}^3\right)$. Biết khối cầu tiếp xúc với tất cả đường sinh của hình nón và đúng một nửa khối cầu chìm trong nước. Tính thể tích nước còn lại trong bình.

A. $27\pi d{m}^3$

B. $6\pi d{m}^3$

C. $9\pi d{m}^3$

D. $24\pi d{m}^3$

Bài 8: Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60 cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu?

A. $V=\frac{1600\sqrt{2}}{3}l$

B. $V=\frac{16\sqrt{2}\pi }{3}l$

C. $V=\frac{16000\sqrt{2}\pi }{3}l$

D. $V=\frac{160\sqrt{2}\pi }{3}l$

Bài 9: Một chiếc bút chì dạng khối lăng trụ lục giác đều có cạnh đáy là 3 mm và chiều cao 200 mm. Thân bút được làm bằng gỗ và phần lõi bằng than chì. Phần lõi dạng khối trụ chiều cao bằng chiều cao của bút và đáy hình tròn có bán kính 1 mm. Giả định $1m^3$gỗ có giá a triệu đồng, $1m^3$ than chì có giá 7a triệu đồng. Khi đó giá nguyên liệu làm một chiếc bút chì như trên gần nhất với kết quả nào?

A. 85,5a đồng

B. 9,07a đồng

C. 8,45a đồng

D. 90,07a đồng

Bài 10: Một chiếc bút chì dạng khối lăng trụ lục giác đều có cạnh đáy là 3 mm và chiều cao 200 mm. Thân bút được làm bằng gỗ và phần lõi dạng khối trụ chiều cao bằng chiều dài của bút và đáy hình tròn có bán kính 1 mm. Giả định $1m^3$ gỗ có giá a triệu đồng, $1m^3$ than chì có giá 9a triệu đồng. Khi đó giá nguyên liệu làm một chiếc bút chì như trên gần nhất với kết quả nào?

A. 103,3a đồng

B. 97,03a đồng

C. 10,33a đồng

D. 9,7a đồng