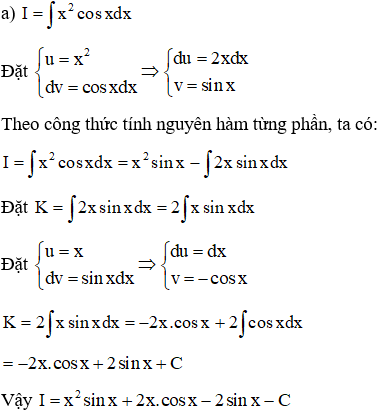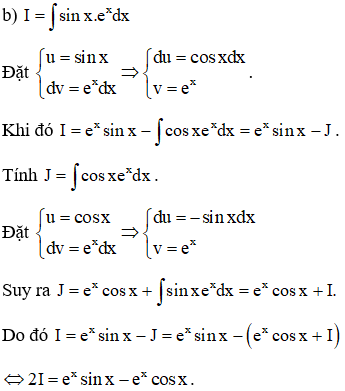100 công thức về nguyên từng phần, đẩy đủ, chi tiết nhất (2024) và cách giải các dạng toán
Công thức và cách giải các dạng toán về nguyên hàm từng phần gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về nguyên hàm từng phần. Mời các bạn đón xem:
Công thức nguyên hàm từng phần đầy đủ, chi tiết nhất
I. Lý thuyết
Định lí: Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x)v'
Hay
II. Phương pháp giải
a) Cách 1: Sử dụng định lý trên
+ Bước 1. Chọn u, v sao cho f(x)dx = udv (chú ý dv = v'(x)dx). Sau đó tính và du = u'.dx.
+ Bước 2. Thay vào công thức và tính
Chú ý. Cần phải lựa chọn u và dv hợp lí sao cho ta dễ dàng tìm được v và tích phân dễ tính hơn . Ta thường gặp các dạng sau
Dạng 1. , trong đó P(x) là đa thức. Ta đặt .
Dạng 2. , trong đó P(x) là đa thức. Ta đặt .
Dạng 3. , trong đó P(x) là đa thức. Ta đặt .
Dạng 4. . Ta đặt .
Thứ tự ưu tiên đặt u: “Nhất log, nhì đa, tam lượng, tứ mũ” và dv phần còn lại. Nghĩa là nếu có ln hay logax thì chọn u=lnx hay và dv = còn lại. Nếu không có ln; log thì chọn u = đa thức và dv = còn lại. Nếu không có log, đa thức, ta chọn u = lượng giác,….
b) Cách 2: Sử dụng bảng
Loại 1: Ví dụ:
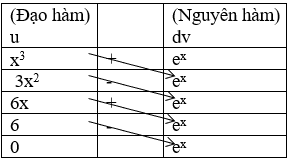
Vậy :
Loại 2: Nguyên hàm lặp. Ví dụ:

Vậy
III. Ví dụ minh họa
Ví dụ 1: Tính các nguyên hàm
a)
b)
Lời giải
a)
Đặt
Theo công thức tính nguyên hàm từng phần, ta có
b)
Đặt
Theo công thức tính nguyên hàm từng phần, ta có:
Ví dụ 2: Tính các nguyên hàm sau:
a)
b)
Lời giải