100 công thức về tính diện tích mặt cầu chi tiết nhất (2024 có đáp án) và cách giải các dạng toán

Công thức tính diện tích mặt cầu chi tiết nhất 

1. Công thức tính diện tích mặt cầu

- Cho mặt cầu (S) có bán kính r.

Khi đó diện tích mặt cầu $S=4\pi r^2$

- Chú ý: Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.

2. Một số ví dụ

VD1. Tính diện tích mặt cầu (S) có bán kính là 3.

Lời giải:

Diện tích mặt cầu là $S=4.\pi {.3}^2=36\pi$

VD2. Cho mặt cầu (S) tâm O có diện tích là $S=100\pi$. Một mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có chu vi là $8\pi$. Tính khoảng cách từ O tới (P).

Lời giải:

Diện tích mặt cầu (S) là: $S=4\pi r^2=100\pi \Rightarrow r=5$

Bán kính của đường tròn thiết diện là $r\text{'}=\frac{8\pi }{2\pi }=4$

Suy ra :

$$\begin{gathered} d\left(O;\left(P\right)\right)=\sqrt{r^2-r{\text{'}}^2} \\ =\sqrt{5^2-4^2}=3 \end{gathered}$$

VD3. Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Tính diện tích mặt cầu ngoại tiếp hình lăng trụ đã cho.

Lời giải:

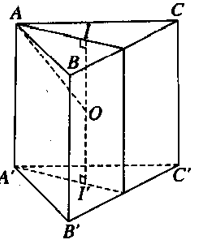
Gọi I và I’ lần lượt là trọng tâm của hai đáy lăng trụ. Suy ra I và I’ đồng thời cũng là tâm của 2 đường tròn ngoại tiếp các tam giác đáy.

Do ABC.A’B’C’ là lăng trụ đều nên II’ chính là trục của lăng trụ

Do đó tâm O của mặt cầu ngoại tiếp nằm trên II’.

Kẻ đường trung trực d của AA’. Dễ thấy d cắt II’ tại trung điểm của II’

Vậy O là trung điểm của II’ $\Rightarrow OI=\frac{a}{2}$

Ta có :

$$\begin{gathered} AI=\frac{a\sqrt{3}}{3} \\ \Rightarrow OA=\sqrt{O{I}^2+A{I}^2} \\ =\sqrt{\frac{a^2}{3}+\frac{a^2}{4}}=\frac{a\sqrt{21}}{6} \end{gathered}$$

Do đó diện tích mặt cầu :

$S=4\pi .{\left(\frac{a\sqrt{21}}{6}\right)}^2=\frac{7a^2\pi }{3}$

VD4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Đường cao $SO=a\sqrt{2}$

Xác định tâm, bán kính và tính diện tích mặt cầu nội tiếp hình chóp S.ABCD.

Lời giải:

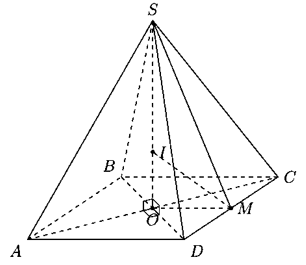
Gọi O là tâm hình vuông ABCD.

Gọi I là tâm mặt cầu nội tiếp hình chóp S.ABCD $\Rightarrow I\in SO$

Do I là tâm mặt cầu nội tiếp nên $d\left(I,\left(ABCD\right)\right)=d\left(I,\left(SCD\right)\right)=r$ tức là MI là phân giác của $\widehat{SMO}$

Theo tính chất đường phân giác ta có tỉ số:

$$\begin{gathered} \frac{IS}{IO}=\frac{SM}{OM} \\ \iff \frac{I\text{}S+IO}{IO}=\frac{SM+OM\text{}}{OM} \\ \iff \frac{SO}{IO}=\frac{SM+OM}{OM} \end{gathered}$$

Ta có:

$$\begin{gathered} OM=\frac{a}{2} \\ \Rightarrow SM=\sqrt{S{O}^2+O{M}^2} \\ =\sqrt{2a^2+\frac{a^2}{4}}=\frac{3a}{2} \end{gathered}$$

Suy ra:

$$\begin{gathered} \frac{SO}{IO}=\frac{\frac{3a}{2}+\frac{a}{2}}{\frac{a}{2}}=4 \\ \iff IO=\frac{a\sqrt{2}}{4} \end{gathered}$$

Vậy mặt cầu nội tiếp hình chóp là mặt cầu $\left(I;\frac{a\sqrt{2}}{4}\right)$

Diện tích mặt cầu là:

$S=4\pi .{\left(\frac{a\sqrt{2}}{4}\right)}^2=\frac{\pi a^2}{2}$