100 công thức tính thể tích khối tròn xoay, đẩy đủ, chi tiết nhất (2024) và cách giải các dạng toán
Công thức và cách giải các dạng toán về tính thể tích khối tròn xoay gồm phương pháp giải, ví dụ minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về tính thể tích khối tròn xoay. Mời các bạn đón xem:
Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất
1. Lý thuyết
* Quay quanh trục Ox:
Hình giới hạn bởi đường cong y = f(x), trục Ox và hai đường thẳng x = a, x = b (trong đó f(x) liên tục trên đoạn [a;b]) quay quanh trục Ox, ta được khối tròn xoay.
Thể tích của khối tròn xoay được tính theo công thức:
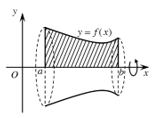
Hình giới hạn bởi hai đường cong y = f(x), y = g(x) và hai đường thẳng x = a, x = b (trong đó f(x), g(x) liên tục trên đoạn [a;b]) quay quanh trục Ox.
Thể tích của khối tròn xoay được tính theo công thức:
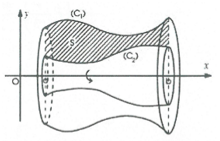
* Quay quanh trục Oy:
Hình giới hạn bởi đường cong x = f(y), trục Oy và hai đường thẳng y = c; y = d (trong đó f(x) liên tục trên đoạn [c; d]) quay quanh trục Oy, ta được khối tròn xoay.
Thể tích của khối tròn xoay được tính theo công thức:
2. Ví dụ minh họa
Ví dụ 1: Tính thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường y = sin x, trục hoành, hai đường thẳng quay quanh trục hoành?
Lời giải
Hình phẳng giới hạn bởi các đường quay quanh trục Ox nên có thể tích:
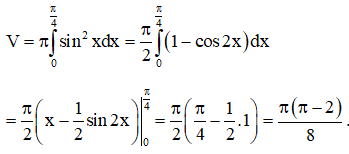
Ví dụ 2: Cho hình phẳng H giới hạn bởi các đường: . Tính thể tích khối tròn xoay được tạo thành khi quay H quanh trục hoành?
Lời giải
Phương trình hoành độ giao điểm của hai đường:
Thể tích khối tròn xoay được tạo bởi hai đường là: