100 công thức chứng minh hai mặt phẳng song song (2024 có đáp án) và cách giải các dạng toán

Công thức Chứng minh hai mặt phẳng song song 

1. Lý thuyết

a) Định nghĩa

Hai mặt phẳng  được gọi là song song với nhau nếu chúng không có điểm chung.

Tức là: $\left(\alpha \right)//\left(\beta \right)$$\iff \left(\alpha \right)\cap \left(\beta \right)=\varnothing$

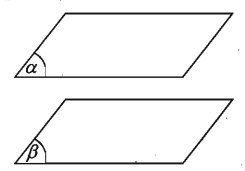
b) Tính chất

Định lý 1:

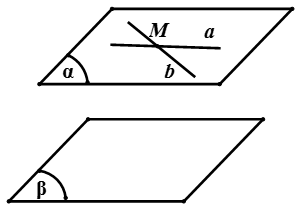
Nếu mặt phẳng $\left(\alpha \right)$ chứa hai đường thẳng cắt nhau  và hai đường thẳng này cùng song song với mặt phẳng $\left(\beta \right)$ thì $\left(\alpha \right)//\left(\beta \right)$.

Tức là:$\left\{\begin{array}{l}a,b\subset \left(\alpha \right)\\ a\cap b=M\\ a//\left(\beta \right)\\ b//\left(\beta \right)\end{array}\right.$$\Rightarrow \left(\alpha \right)//\left(\beta \right)$

Định lý 2:

Qua một điểm nằm ngoài mặt phẳng có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

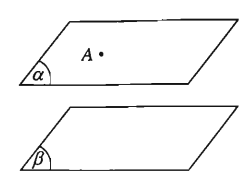
Hệ quả 1:

Nếu $d//\left(\alpha \right)$ thì trong $\left(\alpha \right)$ có một đường thẳng song song với d và qua d có duy nhất một mặt phẳng song song với $\left(\alpha \right)$.

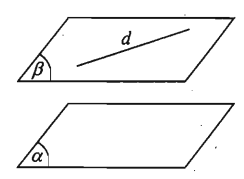
Hệ quả 2:

Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song.

Tức là:$\left\{\begin{array}{l}\left(\alpha \right)//\left(\gamma \right)\\ \left(\beta \right)//\left(\gamma \right)\\ \left(\alpha \right)\ne \left(\beta \right)\end{array}\right.$$\Rightarrow \left(\alpha \right)//\left(\beta \right)$

Hệ quả 3:

Cho điểm A không nằm trên mặt phẳng $\left(\alpha \right)$. Mọi đường thẳng đi qua A và song song với $\left(\alpha \right)$ đều nằm trong mặt phẳng qua A song song với $\left(\alpha \right)$.

Tức là:$\left\{\begin{array}{l}A\notin \left(\alpha \right)\\ A\in d\\ d//\left(\alpha \right)\end{array}\right.$$\Rightarrow \left\{\begin{array}{l}d\subset \left(\beta \right)\\ A\in \left(\beta \right)//\left(\alpha \right)\end{array}\right.$

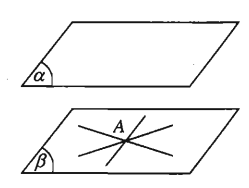
Định lý 3:

Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến đó song song với nhau.

Tức là:$\left\{\begin{array}{l}\left(\alpha \right)//\left(\beta \right)\\ \left(\gamma \right)\cap \left(\alpha \right)=a\\ \left(\gamma \right)\cap \left(\beta \right)=b\end{array}\right.$$\Rightarrow b//a$

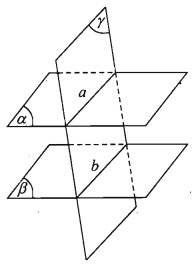
Hệ quả:

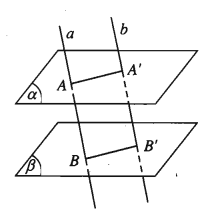
Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau

$\left\{\begin{array}{l}\left(\alpha \right)\text{//}\left(\beta \right)\\ a\cap \left(\alpha \right)=A,\text{ a}\cap \left(\beta \right)=B\\ b\cap \left(\alpha \right)=A^{\text{'}},\text{ b}\cap \left(\beta \right)=B^{\text{'}}\\ \text{a//b}\end{array}\right.$

$\Rightarrow AB=A\text{'}B\text{'}$

2. Công thức

Phương pháp chứng minh hai mặt phẳng song song

Dựa vào định lý 1 và hệ quả như sau:

Định lý 1:$\left\{\begin{array}{l}a,b\subset \left(\alpha \right)\\ a\cap b=M\\ a//\left(\beta \right)\\ b//\left(\beta \right)\end{array}\right.$$\Rightarrow \left(\alpha \right)//\left(\beta \right)$

Hệ quả 2 (của định lý 1):$\left\{\begin{array}{l}\left(\alpha \right)//\left(\gamma \right)\\ \left(\beta \right)//\left(\gamma \right)\\ \left(\alpha \right)\ne \left(\beta \right)\end{array}\right.$$\Rightarrow \left(\alpha \right)//\left(\beta \right)$

3. Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, gọi M, N lần lượt là trung điểm của SA, SD. Chứng minh (OMN) // (SBC).

Lời giải

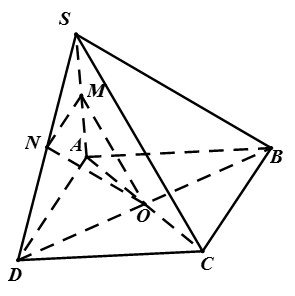
+ Vì O là tâm của hình bình hành ABCD nên O là trung điểm của AC và BD

+ Xét tam giác SBD có N, O là trung điểm của SD và BD

Nên NO là đường trung bình của tam giác SBD.

Do đó NO // SB mà $SB\subset \left(SBC\right)$ nên NO // (SBC)

+ Tương tự MO // SC (Vì MO là đường trung bình của tam giác SAC)

Mà $SC\subset \left(SBC\right)$ nên MO // (SBC)

Ta có: $\left\{\begin{array}{l}NO,MO\subset \left(MNO\right)\\ NO\cap MO=O\\ NO//\left(SBC\right)\\ MO//\left(SBC\right)\end{array}\right.$

$\Rightarrow \left(MNO\right)//\left(SBC\right)$

Ví dụ 2: Cho hình chóp S.ABC có M, N, P lần lượt là trung điểm SA, SB, SC.

a) Chứng minh (MNP) // (ABC).

b) Gọi H, G, L lần lượt là trọng tâm tam giác SAB, SAC, SBC. Chứng minh (HGL) // (MNP).

Lời giải

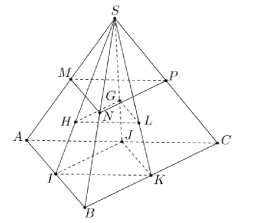
a) Ta có

MN là đường trung bình của tam giác SAB nên MN // AB mà $AB\subset \left(ABC\right)$nên MN // (ABC)

NP là đường trung bình của tam giác SBC nên NP // BC mà $BC\subset \left(ABC\right)$nên NP // (ABC)

Ta có:$\left\{\begin{array}{l}MN,NP\subset \left(MNP\right)\\ MN\cap NP=N\\ MN//\left(ABC\right)\\ NP//\left(ABC\right)\end{array}\right.$$\Rightarrow \left(MNP\right)//\left(ABC\right)$

b) Gọi I, J, K lần lượt là trung điểm của AB, AC, BC

Vì H, G, L lần lượt là trọng tâm tam giác SAB, SAC, SBC nên $\frac{SH}{SI}=\frac{SG}{SJ}=\frac{SL}{SK}=\frac{2}{3}$

Xét tam giác SIJ có $\frac{SH}{SI}=\frac{SG}{SJ}=\frac{2}{3}$ nên HG // IJ mà $IJ\subset \left(ABC\right)$ nên HG // (ABC)

Tương tự HL // IK mà $IK\subset \left(ABC\right)$ nên HL // (ABC)

Ta có:$\left\{\begin{array}{l}HG,HL\subset \left(HGL\right)\\ HG\cap HL=H\\ HG//\left(ABC\right)\\ HL//\left(ABC\right)\end{array}\right.$$\Rightarrow \left(HGL\right)//\left(ABC\right)$

Lại có (MNP) // (ABC) nên (HGL) // (MNP).

4. Bài tập tự luyện

Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, AD, SA. Mặt phẳng (MNP) song song với mặt phẳng nào dưới đây:

A. (MNP) // (SBC)

B. (MNP) // (SCD)

C. (MNP) // (SBD)

D. (MNP) // (SAC)

Câu 2. Cho lăng trụ ABC.A’B’C’. Gọi M, N, H lần lượt là trung điểm của AB, AC, A’B’. Khẳng định nào sau đây là đúng?

A. (AHC’) // (MB’C)

B. (AHC’) // (BB’C’C)

C. (AHC’) // (MB’C’)

D. (AHC’) // (MNB)

Đáp án: 1C, 2A