100 bài tập về vị trí tương đối trong tọa độ không gian (2024 có đáp án) và cách giải các dạng toán

Bài toán về vị trí tương đối trong tọa độ không gian và cách giải 

I. LÝ THUYẾT

Trong không gian Oxyz ta xét các vị trí tương đối:

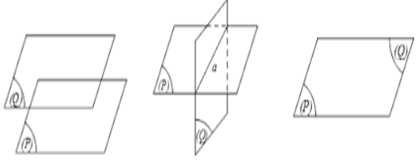
1. Giữa hai mặt phẳng bao gồm 3 vị trí tương đối:

+) Song song.

+) Cắt nhau (trong trường hợp này có bao gồm 2 mặt phẳng vuông góc).

+) Trùng nhau.

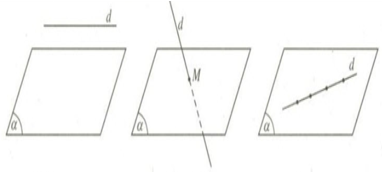
2. Giữa đường thẳng và mặt phẳng bao gồm 3 vị trí tương đối:

+) Song song.

+) Cắt nhau.

+) Đường thẳng nằm trong mặt phẳng.

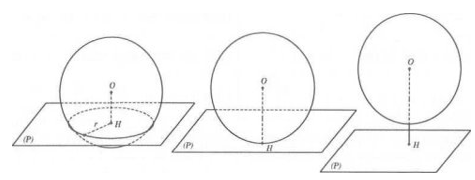
3. Giữa mặt cầu và mặt phẳng bao gồm 3 vị trí tương đối:

+) Cắt nhau (giao tuyến là một hình tròn).

+) Tiếp xúc nhau.

+) Không có điểm chung.

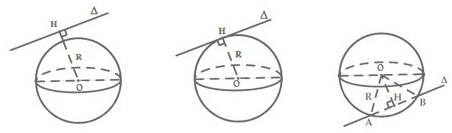
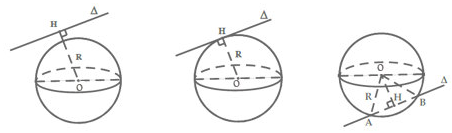
4. Giữa đường thẳng và mặt cầu bao gồm 3 vị trí tương đối:

+) Không cắt nhau.

+) Tiếp xúc nhau.

+) Đường thẳng cắt mặt cầu tại hai điểm phân biệt.

5. Giữa đường thẳng và đường thẳng bao gồm 4 vị trí tương đối:

+) Song song.

+) Cắt nhau.

+) Trùng nhau.

+) Chéo nhau.

II. PHƯƠNG PHÁP GIẢI VÀ VÍ DỤ MINH HỌA

1. Vị trí tương đối của hai mặt phẳng

Phương pháp giải:

Trong không gian Oxyz, cho hai mặt phẳng

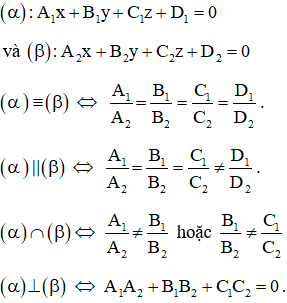
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 2x – 3y + 4z + 30 = 0 và (Q): 4x – 6y + 8z + 40 = 0. Vị trí tương đối của (P) và (Q) là

A. Song song

B. Trùng nhau

C. Cắt nhưng không vuông góc.

D. Vuông góc.

Hướng dẫn giải

Vì $\frac{2}{4}=\frac{-3}{-6}=\frac{4}{8}\ne \frac{30}{40}$ nên (P) // (Q).

Chọn A.

2. Vị trí tương đối của đường thẳng và mặt phẳng:

Phương pháp giải:

Cho đường thẳng: $d:\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{3}t\end{array}\right.$ và mặt phẳng $\left(\alpha \right):$ Ax + By + Cz + D = 0.

Xét hệ phương trình:

$\left\{\begin{array}{ll}x=x_0+a_{1}t& \left(1\right)\\ y=y_0+a_{2}t& \left(2\right)\\ z=z_0+a_{3}t& \left(3\right)\\ Ax+By+Cz+D=0& \left(4\right)\end{array}\right.(*)$

+) (*) có nghiệm duy nhất d cắt $\left(\alpha \right)$

+) (*) vô nghiệm d // $\left(\alpha \right)$

+) (*) vô số nghiệm d $\subset \left(\alpha \right)$

Ví dụ 2: Trong không gian Oxyz, cho mặt phẳng (P): 3x – 3y + 2z – 5 = 0 và đường thẳng $d:\left\{\begin{array}{l}x=-1+2t\\ y=3+4t\\ z=3t\end{array}\right.$ . Trong các mệnh đề sau, mệnh đề nào đúng?

A. d // (P).

B. $d\subset \left(P\right)$.

C. d cắt (P)

D. $d\perp \left(P\right)$

Hướng dẫn giải

Cách 1:

Ta giải hệ PT:

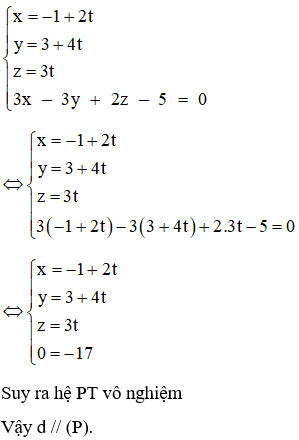
Cách 2:

Mặt phẳng (P) có VTPT $\overrightarrow{a}=\left(3;-3;2\right)$.

d có VTCP $\overrightarrow{b}=\left(2;4;3\right)$.

Ta có:

$\left\{\begin{array}{l}\overrightarrow{a}.\overrightarrow{b}=0\\ A\left(-1;3;0\right)\in d\\ A\notin \left(P\right)\end{array}\right.\Rightarrow d//\left(P\right)$

Chọn A.

3. Vị trí tương đối của mặt cầu và mặt phẳng:

Phương pháp giải:

Cho mặt cầu:$\left(S\right):{\left(x–a\right)}^2+{\left(y–b\right)}^2+{\left(z–c\right)}^2=R^2$

tâm I (a; b; c) bán kính R và mặt phẳng (P): Ax + By + Cz + D = 0.

+) Nếu d (I; (P)) > R thì (P) và mặt cầu (S) không có điểm chung.

+) Nếu d (I; (P)) = R thì mặt phẳng (P) và mặt cầu (S) tiếp xúc nhau. Khi đó (P) gọi là tiếp diện của mặt cầu (S) và điểm chung gọi là tiếp điểm.

+) Nếu d (I; (P)) < R thì mặt phẳng (P) và mặt cầu (S) cắt nhau theo giao tuyến là đường tròn có phương trình:

$\left\{\begin{array}{l}{\left(x-a\right)}^2+{\left(y-b\right)}^2+{\left(z-c\right)}^2=R^2\\ Ax+By+Cz+D=0\end{array}\right.$

Trong đó $r=\sqrt{R^2-d{(I,(P\left)\right)}^2}$ bán kính đường tròn và tâm H của đường tròn là hình chiếu của tâm I mặt cầu (S) lên mặt phẳng (P).

Ví dụ 3: Trong không gian Oxyz, cho mặt cầu (S) có tâm I (2; 1; -1) tiếp xúc với mặt phẳng (P): 2x – 2y – z + 3= 0. Mặt cầu (S) có bán kính R bằng:

A. R = 1

B. R = 2

C. $R=\frac{2}{3}$

D. $R=\frac{2}{9}$

Hướng dẫn giải

(S) tiếp xúc (P)

$$\begin{gathered} R=d\left(I;\left(P\right)\right) \\ =\frac{|2.2-2.1-1.\left(-1\right)+3|}{\sqrt{2^2+{\left(-2\right)}^2+{\left(-1\right)}^2}}=2 \end{gathered}$$

Chọn B.

4. Vị trí tương đối của đường thẳng và mặt cầu

Phương pháp giải:

Cho mặt cầu (S) có tâm I, bán kính R và đường thẳng .

Để xét vị trí tương đối giữa $\Delta$ và (S) ta tính $d\left(I,\Delta \right)$ rồi so sánh với bán kính R.

+) $d\left(I,\Delta \right)>R$: $\Delta$ không cắt (S)

+) $d\left(I,\Delta \right)=R$: $\Delta$ tiếp xúc với (S).

Tiếp điểm J là hình chiếu vuông góc của tâm I lên đường thẳng $\Delta$.

+) $d\left(I,\Delta \right)<R$: $\Delta$ cắt (S) tại hai điểm phân biệt A, B và $R=\sqrt{d^2+\frac{A{B}^2}{4}}$

Ví dụ 4: Trong không gian Oxyz, cho đường thẳng $d:\frac{x}{2}=\frac{y-1}{1}=\frac{z-2}{-1}$và mặt cầu $\left(S\right):x^2+y^2+z^2-2x+4z+1=0$. Số điểm chung của d và (S) là:

A. 0.

B. 1

C. 2.

D. 3.

Hướng dẫn giải.

Ta có: $d:\frac{x}{2}=\frac{y-1}{1}=\frac{z-2}{-1}$

Do đó đường thẳng d đi qua M (0; 1; 2) và có VTCP $\overrightarrow{u}=\left(2;1;-1\right)$

Mặt cầu (S) có tâm I (1; 0; -2) và bán kính R = 2.

Ta có:

$\overrightarrow{MI}=\left(1;-1;-4\right)$

và $\left[\overrightarrow{u},\overrightarrow{MI}\right]=\left(-5;7;-3\right)$

$$\begin{gathered} \Rightarrow d\left(I,d\right)=\frac{\left|\left[\overrightarrow{u},\overrightarrow{MI}\right]\right|}{\left|\overrightarrow{u}\right|} \\ =\frac{\sqrt{{\left(-5\right)}^2+7^2+{\left(-3\right)}^2}}{\sqrt{2^2+1^2+{\left(-1\right)}^2}} \\ =\frac{\sqrt{498}}{6} \end{gathered}$$

Vì d (I, d) > R nên d không cắt mặt cầu (S).

Vậy d và (S) không có điểm chung.

Chọn A.

5. Vị trí tương đối của hai đường thẳng:

Phương pháp giải:

Cho 2 đường thẳng:

$d:\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{3}t\end{array}\right.$ qua M, có VTCP $\overrightarrow{u_d}$

$d\text{'}:\left\{\begin{array}{l}x={x^{\text{'}}}_0+{a^{\text{'}}}_1{t}^{\text{'}}\\ y=y_0+{a^{\text{'}}}_2{t}^{\text{'}}\\ z=z_0+{a^{\text{'}}}_3{t}^{\text{'}}\end{array}\right.$ có VTCP $\overrightarrow{u_{d\text{'}}}$

Khi đó ta có 2 trường hợp:

a) Nếu $\overrightarrow{u_d}$ cùng phương với $\overrightarrow{u_{d\text{'}}}$ ta có:

+) d song song d’

$\iff \left\{\begin{array}{l}\overrightarrow{u_d}=k\overrightarrow{u_{d\text{'}}}\\ M\in d\\ M\notin d\text{'}\end{array}\right.$

+) d trùng d’

$\iff \left\{\begin{array}{l}\overrightarrow{u_d}=k\overrightarrow{u_{d\text{'}}}\\ M\in d\\ M\in d\text{'}\end{array}\right.$

b) Nếu $\overrightarrow{u_d}$ không cùng phương với $\overrightarrow{u_{d\text{'}}}$ ta xét hệ phương trình:

$\left\{\begin{array}{l}{x}_0+a_{1}t={x^{\text{'}}}_0+{a^{\text{'}}}_1{t}^{\text{'}}\\ y_0+a_{2}t=y_0+{a^{\text{'}}}_2{t}^{\text{'}}\\ z_0+a_{3}t=z_0+{a^{\text{'}}}_3{t}^{\text{'}}\end{array}\right.(*)$

+) Nếu phương trình (*) có nghiệm duy nhất thì d cắt d’

+) Nếu phương trình (*) vô nghiệm thì d và d’ chéo nhau.

Ví dụ 5: Trong không gian Oxyz, cho hai đường thẳng $d:\frac{x-1}{2}=\frac{y-7}{1}=\frac{z-3}{4}$ và $d\text{'}:\frac{x-6}{3}=\frac{y+1}{-2}=\frac{z+2}{1}$. Khi đó hai đường thẳng d và d’

A. song song.

B. trùng nhau.

C. cắt nhau.

D. chéo nhau.

Hướng dẫn giải

d có vectơ chỉ phương là $\overrightarrow{u_d}=\left(2;1;4\right)$

d’ có vectơ chỉ phương là $\overrightarrow{u_{d\text{'}}}=\left(3;-2;1\right)$

Suy ra d và d’ không cùng phương.

$d:\left\{\begin{array}{l}x=1+2t\\ y=7+t\\ z=3+4t\end{array}\right.$,

$d\text{'}:\left\{\begin{array}{l}x=6+3t\text{'}\\ y=-1-2t\text{'}\\ z=-2+t\text{'}\end{array}\right.$

Ta xét hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{l}1+2t=6+3t\text{'}\\ 7+t=-1-2t\text{'}\\ 3+4t=-2+t\text{'}\end{array}\right. \\ \iff \left\{\begin{array}{l}t=-2\\ t\text{'}=-3\end{array}\right. \end{gathered}$$

Khi đó hệ phương trình có nghiệm duy nhất.

Vậy d và d’ cắt nhau.

Chọn C.

III. BÀI TẬP ÁP DỤNG

Câu 1. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 2x – 3y + 4z + 20 = 0 và (Q): 6x – 9y + 12z + 40 = 0. Vị trí tương đối của (P) và (Q) là:

A. Song song.

B. Trùng nhau

C. Cắt nhưng không vuông góc

D. Vuông góc.

Câu 2. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 2x – 3y + 4z + 20 = 0 và (Q): 6x – 9y + 12z + 60 = 0. Vị trí tương đối của (P) và (Q) là:

A. Song song

B. Trùng nhau

C. Cắt nhưng không vuông góc

D. Vuông góc.

Câu 3: Trong không gian Oxyz, cho hai mặt phẳng (P): 2x + my + 2mz – 9 = 0 và (Q): 6x – y – z – 10 = 0. Tìm m để $\left(P\right)\perp \left(Q\right)$.

A. m = 4

B. m = -4

C. m = -2

D. m = 2.

Câu 4: Trong không gian Oxyz, cho mặt phẳng (P): 3x – 3y + 2z – 6 = 0 và đường thẳng $d:\left\{\begin{array}{l}x=1+2t\\ y=3+4t\\ z=3+3t\end{array}\right.$. Trong các mệnh đề sau, mệnh đề nào đúng?

A. d // (P).

B. $d\subset \left(P\right)$

C. d cắt (P).

D. $d\perp \left(P\right)$

Câu 5: Trong không gian Oxyz, cho mặt phẳng (P): x + y + z – 4 = 0 và đường thẳng $d:\left\{\begin{array}{l}x=1+t\\ y=1+2t\\ z=2-3t\end{array}\right.$. Số giao điểm của đường thẳng d và mặt phẳng (P) là:

A. Vô số.

B. 1

C. Không có

D. 2.

Câu 6: Trong không gian Oxyz, cho hai đường thẳng $d:\left\{\begin{array}{l}x=1+2t\\ y=2-2t\\ z=t\end{array}\right.$ và $d\text{'}:\left\{\begin{array}{l}x=-2t\\ y=-5+3t\\ z=4+t\end{array}\right.$. Khi đó hai đường thẳng d và d’

A. song song

B. trùng nhau

C. chéo nhau.

D. cắt nhau.

Câu 7: Trong không gian Oxyz, hai đường thẳng $d:\frac{x-1}{-2}=\frac{y+2}{1}=\frac{z-4}{3}$ và $d\text{'}:\left\{\begin{array}{l}x=-1+t\\ y=-t\\ z=-2+3t\end{array}\right.$có vị trí tương đối là:

A. trùng nhau.

B. song song

C. chéo nhau

D. cắt nhau.

Câu 8: Trong không gian Oxyz, cho mặt phẳng (P): 2x – 2y – z – 3 = 0 và điểm I (1; 0; 2). Phương trình mặt cầu tâm I tiếp xúc với mặt phẳng (P) là:

A. ${\left(x-1\right)}^2+y^2+{\left(z-2\right)}^2=1$

B. ${\left(x+1\right)}^2+y^2+{\left(z+2\right)}^2=1$

C. ${\left(x+1\right)}^2+y^2+{\left(z+2\right)}^2=3$

D. ${\left(x-1\right)}^2+y^2+{\left(z-2\right)}^2=3$

Câu 9: Trong không gian Oxyz, cho đường thẳng $d:\frac{x+5}{2}=\frac{y-7}{-2}=\frac{z}{1}$ và điểm M (4; 1; 6). Đường thẳng d cắt mặt cầu (S) có tâm M, tại hai điểm A, B sao cho AB = 6. Phương trình của mặt cầu (S) là:

A. ${\left(x-4\right)}^2+{\left(y-1\right)}^2+{\left(z-6\right)}^2=9.$

B. ${\left(x+4\right)}^2+{\left(y+1\right)}^2+{\left(z+6\right)}^2=18.$

C. ${\left(x-4\right)}^2+{\left(y-1\right)}^2+{\left(z-6\right)}^2=18.$

D. ${\left(x-4\right)}^2+{\left(y-1\right)}^2+{\left(z-6\right)}^2=16.$

Câu 10: Trong không gian Oxyz, mặt phẳng (P) chứa trục Ox và cắt mặt cầu $\left(S\right):x^2+y^2+z^2-2x+4y+2z-3=0$ theo giao tuyến là đường tròn có bán kính bằng 3 có phương trình là:

A. y – 2z = 0

B. y + 2z = 0

C. y + 3z = 0

D. y – 3z = 0

ĐÁP ÁN