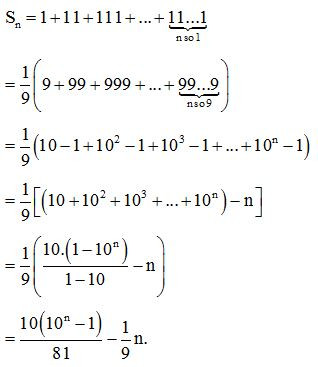100 công thức về tính tổng n số hạng đầu của cấp số nhân (2024 có đáp án) và cách giải các dạng toán

Công thức tính tổng n số hạng đầu của cấp số nhân

1. Lý thuyết

Tổng n số hạng đầu tiên của cấp số nhân được xác định bởi công thức:

$S_n=u_1+u_2+\mathrm{...}+u_n=\frac{u_1\left(1-q^n\right)}{1-q}$

Trong đó, u1 là số hạng đầu tiên, q là công bội của cấp số nhân.

Chú ý: Nếu q = 1 thì cấp số nhân là u1; u1; u1; … u1;.. khi đó Sn = n.u1.

2. Công thức

- Tổng n số hạng đầu tiên: $S_n=\frac{u_1\left(1-q^n\right)}{1-q}$.

- Công thức tính nhanh tổng:

$S=9+99+999+\mathrm{...}+\underset{nsố9}{\underbrace{\mathrm{999..9}}}$$=\frac{10\left({10}^n-1\right)}{9}-n$

3. Ví dụ minh họa

Ví dụ 1: Cho cấp số nhân (un) với u2 = 10 và u5 = 1250.

a) Tính tổng 20 số hạng đầu tiên của cấp số nhân.

b) Tính tổng S = u1 + u3 + u5 +u7 +…+ u99.

Lời giải

a) Ta có:

$$\begin{gathered} \left\{\begin{array}{l}{u}_2=10\\ u_5=1250\end{array}\right.\iff \left\{\begin{array}{l}{u}_{1}q=10\\ u_1{q}^4=1250\end{array}\right. \\ \iff \left\{\begin{array}{l}{q}^3=125=5^3\\ u_{1}q=10\end{array}\right.\iff \left\{\begin{array}{l}q=5\\ u_1=2\end{array}\right. \end{gathered}$$

Tổng của 20 số hạng đầu tiên của cấp số nhân:

$S_{20}=\frac{u_1\left(1-q^n\right)}{1-q}=\frac{2.\left[1-5^{20}\right]}{1-5}=\frac{1}{2}.\left(5^{20}-1\right)$

b) Dãy số u1; u3; u5; u7; … u99 là cấp số nhân với số hạng đầu tiên là u1 = 2 và công bội $q\text{'}=\frac{u_3}{u_1}=q^2=25$.

Dãy số đó có: $\frac{99-1}{2}+1=50$ số hạng

Tổng

$$\begin{gathered} S=u_1+u_3+u_5+u_7+\dots +u_{99} \\ =\frac{2\left(1-{25}^{50}\right)}{1-25}=\frac{1}{12}.\left({25}^{50}-1\right) \\ =\frac{1}{12}.\left(5^{100}-1\right) \end{gathered}$$.

Ví dụ 2:  Tính tổng: $S_n=1+11+111+\mathrm{...}+\underset{nso1}{\underbrace{\mathrm{11...1}}}$.

Lời giải