100 bài tập về hàm số lũy thừa, hàm số mũ, hàm số logarit (2024 có đáp án) và cách giải các dạng toán

Hàm số lũy thừa, hàm số mũ, hàm số logarit và cách giải bài tập

I. LÝ THUYẾT

1. Hàm số mũ

Hàm số có dạng $y=a^x$, $0<a\ne 1$ được gọi là hàm số mũ.

+ Tập xác định: $D=ℝ$.

+ Tập giá trị: $T=\left(0;+\infty \right)$.

+ Sự biến thiên:

Khi a > 1 hàm số đồng biến trên khoảng $\left(-\infty ;+\infty \right)$

Khi 0 < a < 1 hàm số nghịch biến trên khoảng $\left(-\infty ;+\infty \right)$

+ Đồ thị nhận trục hoành làm tiệm cận ngang.

+ Đạo hàm:

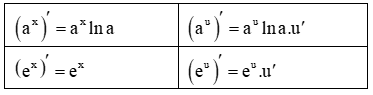
+ Bảng biến thiên và đồ thị:

Với: $y=a^x$, (a > 1)

Bảng biến thiên.

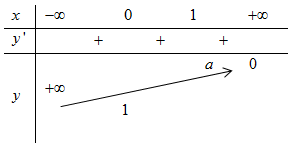
Đồ thị như hình sau.

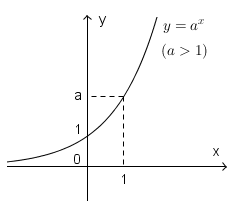
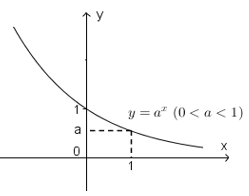
Với: $y=a^x$, (0 < a < 1)

Bảng biến thiên.

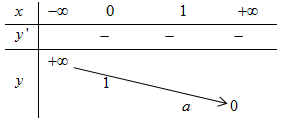
Đồ thị như hình sau.

2. Hàm số lũy thừa

+ Khái niệm: Hàm số $y=x^{\alpha }$, với $\alpha \in ℝ$, được gọi là hàm số lũy thừa.

+ Tập xác định: Tập xác định của hàm số lũy thừa $y=x^{\alpha }$ tùy thuộc vào giá trị của $\alpha$.

Cụ thể:

- Với $\alpha$ nguyên dương, tập xác định là R.

- Với $\alpha$ nguyên âm hoặc bằng 0, tập xác định là $ℝ\backslash \left\{0\right\}$.

- Với không nguyên, tập xác định .

+ Đạo hàm:

${\left(x^{\alpha }\right)}^{\text{'}}=\alpha .x^{\alpha -1}$

u = u(x) $\Rightarrow {\left(u^{\alpha }\right)}^{\text{'}}=\alpha .u^{\text{'}}.u^{\alpha -1}$

+ Sự biến thiên của hàm số $y=x^{\alpha }$ trong khoảng $\left(0;+\infty \right)$

Với > 0: Hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Với < 0: Hàm số nghịch biến trong khoảng $\left(0;+\infty \right)$

+ Đồ thị hàm số $y=x^{\alpha }$ trong khoảng $\left(0;+\infty \right)$

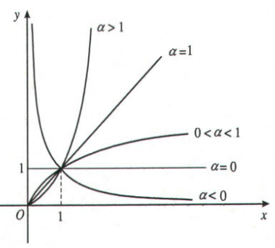
Đồ thị của hàm số lũy thừa $y=x^{\alpha }$ luôn đi qua điểm I(1,1).

3. Hàm số logarit

Hàm số có dạng $y={\log }_{a}x$ $\left(0<a\ne 1\right)$

Tập xác định: $D=\left(0;+\infty \right)$

Tập giá trị: $T=ℝ$.

Đạo hàm:

Sự biến thiên: Khi a > 1 hàm số đồng biến trên khoảng $\left(0;+\infty \right)$,

Khi 0 < a < 1 hàm số nghịch biến trên khoảng $\left(0;+\infty \right)$.

Đồ thị:

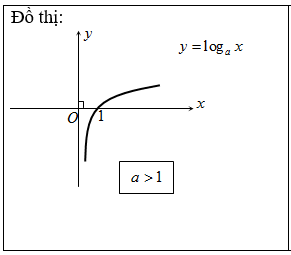
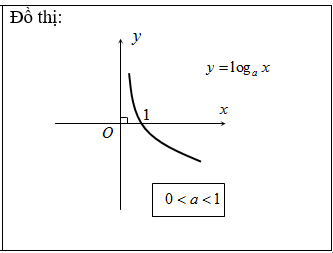
Đồ thị nhận trục tung làm tiệm cận đứng.

II. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1: Tìm tập xác định của hàm số.

A. Phương pháp giải

Bước 1 : Tìm tập xác định của hàm số lũy thừa: $y=u{\left(x\right)}^{\alpha },\forall \alpha \in ℝ$

+ Nếu $\alpha \in {\mathbb{Z}}^{+}$, hàm số xác định khi u(x)xác định.

+ Nếu $\left[\begin{array}{l}\alpha \in {\mathbb{Z}}^{-}\\ \alpha =0\end{array}\right.$, hàm số xác định khi $u\left(x\right)\ne 0$.

+ Nếu $\alpha \notin \mathbb{Z}$, hàm số xác định khi u(x) > 0.

Bước 2 : Tìm tập xác định của hàm số logarit:

Dựa vào định nghĩa logarit logab xác định$\iff \left\{\begin{array}{l}a>0,a\ne 1\\ b>0\end{array}\right.$

B. Ví dụ minh họa

Câu 1. Hàm số $y={\left(x-2\right)}^{\frac{1}{2}}$ có tập xác định là

A. $D=\left[2;+\infty \right)$

B. $D=ℝ$

C. $D=\left(2;+\infty \right)$

D. $D=ℝ\backslash \left\{2\right\}$

Lời giải

Chọn C

Vì $\frac{1}{2}$ không nguyên nên hàm số $y={\left(x-2\right)}^{\frac{1}{2}}$ xác định khi $x-2>0\iff x>2$.

Tập xác định của hàm số là $D=\left(2;+\infty \right)$.

Câu 2. Tập xác định của hàm số $y={\left(x^2-5x+6\right)}^{-2019}$ là

A. $\left(-\infty ;2\right)\cup \left(3;+\infty \right)$

B.(2;3).

C. $R\backslash \left\{2;3\right\}$

D. $\left(-\infty ;2\right]\cup \left[3;+\infty \right)$

Lời giải

Chọn C

Vì -2019 là số nguyên âm nên hàm số $y={\left(x^2-5x+6\right)}^{-2019}$ xác định khi :

$x^2-5x+6\ne 0\iff \left\{\begin{array}{l}x\ne 2\\ x\ne 3\end{array}\right.$

Câu 3.Tìm tập xác định của hàm số $y={\left(x^2-x-2\right)}^{\sqrt{2}}$.

A. $D=ℝ$

B. $D=\left(-\infty ;-1\right]\cup \left[2;+\infty \right)$

C. $D=\left(-\infty ;-1\right)\cup \left(2;+\infty \right)$

D. $D=ℝ\backslash \left\{-1;2\right\}$

Lời giải

Chọn C

Vì $\sqrt{2}$ không nguyên nên hàm số $y={\left(x^2-x-2\right)}^{\sqrt{2}}$ xác định khi:

$x^2-x-2>0\iff \left[\begin{array}{l}x<-1\\ x>2\end{array}\right.$

TXĐ: $D=\left(-\infty ;-1\right)\cup \left(2;+\infty \right)$

Câu 4.Cho hàm số $y=x^{-4}$. Tìm mệnh đề sai trong các mệnh đề sau.

A. Đồ thị hàm số có một trục đối xứng.

B. Đồ thị hàm số đi qua điểm(1,1).

C. Đồ thị hàm số có hai đường tiệm cận.

D. Đồ thị hàm số có một tâm đối xứng.

Lời giải

Chọn D

* TXĐ: $D=ℝ\backslash \left\{0\right\}$.

Ta có: $y=x^{-4}=\frac{1}{x^4}$$\forall x\in D\Rightarrow -x\in D$ và $y\left(-x\right)=\frac{1}{{\left(-x\right)}^4}=\frac{1}{x^4}=y\left(x\right)$ nên hàm số đã cho là hàm số chẵn $\Rightarrow$Đồ thị hàm số nhận trục Oy làm trục đối xứng $\Rightarrow$A đúng.

* Đồ thị hàm số đi qua điểm (1;1) nên B đúng.

* Ta có: $\underset{x\to \pm \infty }{\lim }y=0\Rightarrow$TCN: y = 0;$\underset{x\to 0^{+}}{\lim }y=+\infty \Rightarrow$ TCĐ: x = 0.

Đồ thị hàm số có hai đường tiệm cận nên C đúng.

Câu 5. Tập xác định của hàm số $y={\left(x^3-27\right)}^{\frac{\pi }{2}}$ là

A. $D=\left(3;+\infty \right)$

B. $D=ℝ\backslash \left\{2\right\}$

C. $ℝ$

D. $D=\left[3;+\infty \right)$

Lời giải

Chọn A

Vì $\frac{\pi }{2}$ không nguyên nên hàm số đã cho xác định khi :

$$\begin{gathered} x^3-27>0 \\ \iff x^3>27\iff x>3 \end{gathered}$$

Câu 6. Có bao nhiêu giá trị nguyên của $m\in \left(-2018;2018\right)$ để hàm số $y={\left(x^2-2x-m+1\right)}^{\sqrt{2018}}$ có tập xác định là $D=ℝ$

A. 2017.

B. Vô số.

C. 2018.

D. 2016.

Lời giải

Chọn A

Vì $\sqrt{2018}$ không nguyên nên hàm số $y={\left(x^2-2x-m+1\right)}^{\sqrt{2018}}$ có tập xác định là D khi và chỉ khi $x^2-2x-m+1>0$,

$\forall x\in ℝ\iff x^2-2x+1>m$,

$\forall x\in ℝ\iff {\left(x-1\right)}^2>m$,

$\forall x\in ℝ\iff m<0$.

$$\begin{gathered} m\in \left(-2018;2018\right) \\ \Rightarrow m\in \left(-2018;0\right) \end{gathered}$$

mà m nguyên nên $m\in \left\{-2017;-2016;\mathrm{...};-1\right\}$.Vậy có 2017 giá trị nguyên của m.

Câu 7: Tìm tập xác định D của hàm số $y={\log }_3\left(2x+1\right)$.

A. $D=\left(-\infty ;-\frac{1}{2}\right)$

B. $D=\left(\frac{1}{2};+\infty \right)$

C. $D=\left(0;+\infty \right)$

D. $D=\left(-\frac{1}{2};+\infty \right)$

Lời giải

Chọn D

Hàm số $y={\log }_3\left(2x+1\right)$ có nghĩa khi $2x+1>0\iff x>-\frac{1}{2}$. Vậy TXĐ là $D=\left(-\frac{1}{2};+\infty \right)$

Câu 8: Tìm tập xác định D của hàm số $y={\log }_3\left(x^2+3x+2\right)$

A. D = [-2, -1].

B. $D=\left(-\infty ;-2\right)\cup \left(-1;+\infty \right)$

C. D = (-2, -1).

D. $D=\left(-\infty ;-2\right]\cup \left[-1;+\infty \right)$

Lời giải

Chọn B

Điều kiện $x^2+3x+2>0\iff \left[\begin{array}{l}x<-2\\ x>-1\end{array}\right.$. Vậy tập xác định của hàm số $y={\log }_3\left(x^2+3x+2\right)$ là: $D=\left(-\infty ;-2\right)\cup \left(-1;+\infty \right)$

Câu 9: Hàm số $y={\log }_2\left(-x^2+5x-6\right)$ có tập xác định là:

A. (2, 3).

B. $\left(-\infty ;2\right)\cup \left(3;+\infty \right)$

C. $\left(-\infty ;2\right)$

D. $\left(3;+\infty \right)$

Lời giải

Chọn A

Hàm số có nghĩa khi và chỉ khi $-x^2+5x-6>0\iff$ 2 < x < 3.

Kết luận. Vậy tập xác định là (2; 3).

Câu 10: Tập xác định của hàm số $y=\ln \left(x-1\right)+\ln \left(x+1\right)$ là:

A. $\left(1;+\infty \right)$

B. $\left(-\infty ;\sqrt{2}\right)$

C. $\varnothing$

D. $\left[\sqrt{2};+\infty \right)$

Lời giải

Chọn A

Ta có:

$$\begin{gathered} \left\{\begin{array}{l}x-1>0\\ x+1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x>1\\ x>-1\end{array}\right.\iff x>1 \end{gathered}$$

Kết luận: Vậy tập xác định $D=\left(1;+\infty \right)$.

Dạng 2: Tính đạo hàm của hàm số.

A. Phương pháp giải

B. Ví dụ minh họa

Câu 1. Cho hàm số $y={\left(2x^2+4x+1\right)}^{\sqrt{3}}$. Khi đó đạo hàm y’(0) bằng

A. $4\sqrt{3}$

B. 0.

C. $12\sqrt{3}$

D. 28.

Lời giải

Chọn A

$$\begin{gathered} y={\left(2x^2+4x+1\right)}^{\sqrt{3}} \\ \Rightarrow y^{\text{'}}\left(x\right) \\ =\sqrt{3}.\left(4x+4\right).{\left(2x^2+4x+1\right)}^{\sqrt{3}-1} \\ \Rightarrow y^{\text{'}}\left(0\right)=4\sqrt{3} \end{gathered}$$

Câu 2. Tính đạo hàm của hàm số $y={\left(x^2+1\right)}^{\frac{3}{2}}$

A. $\frac{3}{2}{\left(x^2+1\right)}^{\frac{1}{2}}$

B. $\frac{3}{4}{x}^{\frac{1}{4}}$

C. $\frac{3}{2}{\left(2x\right)}^{\frac{1}{2}}$

D. $3x{\left(x^2+1\right)}^{\frac{1}{2}}$ .

Lời giải

Chọn D

Ta có

$$\begin{gathered} y^{\text{'}}={\left[{\left(x^2+1\right)}^{\frac{3}{2}}\right]}^{\text{'}} \\ =\frac{3}{2}{\left(x^2+1\right)}^{\frac{1}{2}}.{\left(x^2+1\right)}^{\text{'}} \\ =3x{\left(x^2+1\right)}^{\frac{1}{2}} \end{gathered}$$

Câu 3. Cho hàm số $y={\left(x+2\right)}^{-2}$. Gọi y’’ là đạo hàm cấp hai của hàm số y trên tập xác định của hàm số. Khẳng định nào sau đây là đúng?

A. 2y’’ – 3y = 0.

B. ${\left(y^{\text{'}\text{'}}\right)}^2-4y=0$

C. 2y’’ + 2y = 0

D. ${y^{\text{'}}}^{\text{'}}-6y^2=0$

Lời giải

Chọn D

Ta có:

$\begin{array}{l}y={\left(x+2\right)}^{-2}\\ \Rightarrow y^{\text{'}}=-2{\left(x+2\right)}^{-3}\\ \Rightarrow {y^{\text{'}}}^{\text{'}}=6{\left(x+2\right)}^{-4}\end{array}$

Suy ra :

${y^{\text{'}}}^{\text{'}}-6y^2=\frac{6}{{\left(x+2\right)}^4}-6.{\left(\frac{1}{{\left(x+2\right)}^2}\right)}^2=0$

Câu 4: Tính đạo hàm của hàm số $y={\log }_{2017}\left(x^2+1\right)$ .

A. $y^{\text{'}}=\frac{2x}{2017}$

B. $y^{\text{'}}=\frac{2x}{\left(x^2+1\right)\ln 2017}$

C. $y^{\text{'}}=\frac{1}{\left(x^2+1\right)\ln 2017}$

D. $y^{\text{'}}=\frac{1}{\left(x^2+1\right)}$

Lời giải

Chọn B

Ta có

$$\begin{gathered} y^{\text{'}}={\left({\log }_{2017}\left(x^2+1\right)\right)}^{\text{'}} \\ =\frac{{\left(x^2+1\right)}^{\text{'}}}{\left(x^2+1\right)\ln 2017} \\ =\frac{2x}{\left(x^2+1\right)\ln 2017} \end{gathered}$$

Câu 5: Cho hàm số $y=2x{\text{e}}^x+3\sin 2x$. Khi đó y’(0) có giá trị bằng

A. 8.

B. -4.

C. 2.

D. 5.

Lời giải

Chọn A

$$\begin{gathered} y=2x{\text{e}}^x+3\sin 2x \\ {y}^{\text{'}}=2\left({\text{e}}^x+x{\text{e}}^x\right)+6\cos 2x \\ \Rightarrow y^{\text{'}}\left(0\right)=8 \end{gathered}$$

Câu 6: Tính đạo hàm của hàm số $y=2^{\sqrt{1-x}}$.

A. $y^{\text{'}}=\frac{-\ln 2}{2\sqrt{1-x}}{.2}^{\sqrt{1-x}}$

B. $y^{\text{'}}=\frac{\ln 2}{2\sqrt{1-x}}{.2}^{\sqrt{1-x}}$

C. $y^{\text{'}}=\frac{-2^{\sqrt{1-x}}}{2\sqrt{1-x}}$

D. $y^{\text{'}}=\frac{2^{\sqrt{1-x}}}{2\sqrt{1-x}}$

Lời giải

Chọn A

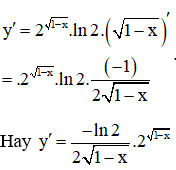
Câu 7: Cho hàm số $y={\text{e}}^x+{\text{e}}^{-x}$. Tính ${y^{\text{'}}}^{\text{'}}\left(1\right)=?$

A. $\text{e}+\frac{1}{\text{e}}$

B. $\text{e}-\frac{1}{\text{e}}$

C. $-\text{e}+\frac{1}{\text{e}}$

D. $-\text{e}-\frac{1}{\text{e}}$

Lời giải

Chọn A

Ta có:

$$\begin{gathered} y^{\text{'}}={\text{e}}^x-{\text{e}}^{-x} \\ \Rightarrow {y^{\text{'}}}^{\text{'}}={\text{e}}^x+{\text{e}}^{-x} \\ \Rightarrow {y^{\text{'}}}^{\text{'}}\left(1\right)=\text{e}+\frac{1}{\text{e}} \end{gathered}$$

Câu 8: Tính đạo hàm của hàm số $y=3^{6x+1}$.

A. $y^{\text{'}}=3^{6x+2}.2$

B. $y^{\text{'}}=3^{6x+2}.2$

C. $y^{\text{'}}=3^{6x+2}.2\ln 3$

D. $y^{\text{'}}=3^{6x+1}.\ln 3$

Lời giải

Chọn C

Ta có:

$$\begin{gathered} y=3^{6x+1} \\ \Rightarrow y^{\text{'}}={\left(6x+1\right)}^{\text{'}}\cdot 3^{6x+1}\ln 3 \\ =6\cdot 3^{6x+1}\ln 3=3^{6x+2}2\ln 3 \end{gathered}$$

Câu 9: Cho hàm số $y=\ln \frac{1}{x+1}.$ Hệ thức nào sau đây đúng?

A. $x{y}^{\text{'}}+1={\text{e}}^y$

B. $x{\text{e}}^y+y^{\text{'}}=0$

C. $x{y}^{\text{'}}+{\text{e}}^y=1$

D. $x{\text{e}}^y+y^{\text{'}}=1$

Lời giải

Chọn A

Ta có:

$$\begin{gathered} y=\ln \frac{1}{x+1}\Rightarrow y^{\text{'}}=-\frac{1}{x+1} \\ x.y^{\text{'}}+1=-\frac{x}{x+1}+1 \\ =\frac{1}{x+1}={\text{e}}^{\ln \frac{1}{x+1}}={\text{e}}^y \end{gathered}$$

Câu 10: Đạo hàm của hàm số $f\left(x\right)=\ln \left(x+\sqrt{x^2+a}\right)+C\left(a>0\right)$ là :

A. $\frac{1}{\sqrt{x^2+a}}$

B. $\frac{1}{x+\sqrt{x^2+a}}$

C. $\sqrt{x^2+a}$

D. $x+\sqrt{x^2+a}$

Lời giải

Chọn A

Áp dụng công thức:

$$\begin{gathered} \left(\ln u^{\text{'}}\right)=\frac{u^{\text{'}}}{u} \\ \Rightarrow f\text{'}\left(x\right)=\frac{{\left(x+\sqrt{x^2+a}\right)}^{\text{'}}}{x+\sqrt{x^2+a}} \\ =\frac{1+\frac{x}{\sqrt{x^2+a}}}{x+\sqrt{x^2+a}}=\frac{1}{\sqrt{x^2+a}} \end{gathered}$$

Dạng 3: Khảo sát sự biến thiên và đồ thị của hàm số.

A. Phương pháp giải

- Sự biến thiên của các hàm số: Áp dụng tính chất:

a) Hàm số lũy thừa  $y=x^{\alpha }$ trong khoảng $\left(0;+\infty \right)$

Với \(\alpha\)> 0: Hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Với \(\alpha\)< 0: Hàm số nghịch biến trong khoảng $\left(0;+\infty \right)$

b) Hàm số mũ: $y=a^x\left(a>0,a\ne 1\right)$. Tập xác định: R.

Nếu a > 1: hàm số luôn đồng biến.

Nếu 0 < a < 1: hàm số luôn nghịch biến.

c) Hàm số logarit $y={\log }_{a}x\left(a>0,a\ne 1\right)$. Tập xác định: $\left(0;+\infty \right)$

Nếu a > 1: hàm số đồng biến $\left(0;+\infty \right)$

Nếu 0 < a < 1: hàm số nghịch biến $\left(0;+\infty \right)$

- Đồ thị của các hàm số.

+Bước 1 : Dựa vào tính đơn điệu của hàm số.

+Bước 2 : Đồ thị của hàm số lũy thừa $y=x^{\alpha }$ luôn đi qua điểm I(1,1).

Đồ thị hàm số mũ $y=a^x$ đi qua điểm $A\left(1;a\right)$.

Đồ thị hàm số đi $y={\log }_{a}x$ qua điểm $B\left(a;1\right)$.

B. Ví dụ minh họa

Câu 1. Hàm số nào sau đây luôn nghịch biến trên tập xác định của nó:

A. $y=x^{\sqrt{3}}$$$

B. $y=x^{\pi }$

C. $y=x^{-\frac{3}{2}}$

D. $y=x^{\sqrt{5}}$

Lời giải

Chọn C

Hàm số có $y=x^{\sqrt{3}}$ tập xác định là $\left(0;+\infty \right)$ và $\alpha =\sqrt{3}$ > 0 nên hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Hàm số có $y=x^{\pi }$ tập xác định là $\left(0;+\infty \right)$ và $\alpha =\pi$> 0 nên hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Hàm số có tập xác định là $\left(0;+\infty \right)$ và $\alpha =-\frac{3}{2}$ < 0 nên hàm số nghịch biến trong khoảng $\left(0;+\infty \right)$

Hàm số có tập xác định là $\left(0;+\infty \right)$ và $\alpha =\sqrt{5}$> 0 nên hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Câu 2. Cho ba hàm số $y=x^{\sqrt{3}}$, $y=x^{\frac{1}{5}}$, $y=x^{-2}$. Khi đó đồ thị của ba hàm số $y=x^{\sqrt{3}}$$y=x^{\frac{1}{5}}$ ,$y=x^{-2}$ lần lượt là

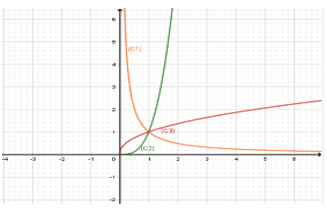
A. (C3), (C2), (C1).

B. (C2), (C3), (C1).

C. (C2), (C1), (C3).

D. (C1), (C3), (C2).

Lời giải

Chọn B

Nhìn vào đồ thị (C1) ta thấy nó đi xuống từ trái sang phải. Là đồ thị của hàm số nghịch biến nên nó là đồ thị của hàm số $y=x^{-2}$.

Vì $\sqrt{3}>1$ nên đồ thị của hàm số $y=x^{\sqrt{3}}$ là (C2)

Do đó (C3) là đồ thị của hàm số $y=x^{\frac{1}{5}}$; Vậy đáp án là: B

Câu 3: Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. $y={\log }_2\left(1-x\right)$

B. $y={2017}^{2-x}$

C. $y={\log }_{\frac{1}{2}}\left(3-x\right)$

D. $y={\left(\frac{\sqrt{3}}{2}\right)}^{x+1}$

Lời giải

Chọn C

Hàm số $y={\log }_{\frac{1}{2}}\left(3-x\right)$ có TXĐ $D=\left(-\infty ;3\right)$

Ta có :

$$\begin{gathered} y^{\text{'}}=\frac{{\left(3-x\right)}^{\text{'}}}{\left(3-x\right).\ln \left(\frac{1}{2}\right)} \\ =\frac{-1}{\left(3-x\right).\ln \left(\frac{1}{2}\right)}>0,\forall x<3 \end{gathered}$$

Câu 4: Hàm số nào sau đây nghịch biến trên tập xác định của nó?

A. $y={\log }_{\frac{\text{e}}{\pi }}x$

B. $y={\log }_{\sqrt{3}}x$

C. $y={\log }_{2}x$

D. $y={\log }_{\pi }x$

Lời giải

Chọn A

Xét hàm $y={\log }_{\frac{\text{e}}{\pi }}x$ có TXĐ: $D=\left(0;+\infty \right)$

Vì $0<\frac{e}{\pi }<1$ nên $y={\log }_{\frac{\text{e}}{\pi }}x$ là hàm nghịch biến trên tập xác định D.

Câu 5: Cho hàm số $y={\left(\frac{3}{4}\right)}^{x^2-2x+2}$. Trong các khẳng định dưới đây, khẳng định nào đúng?

A. Hàm số luôn đồng biến trên R.

B. Hàm số luôn nghịch biến trên khoảng $\left(-\infty ;1\right)$.

C. Hàm số luôn đồng biến trên trên $\left(-\infty ;1\right)$.

D. Hàm số luôn nghịch biến trên R.

Lời giải

Chọn C

$y^{\text{'}}=\left(2x-2\right){\left(\frac{3}{4}\right)}^{x^2-2x+2}\ln \frac{3}{4}$

$y^{\text{'}}=0\iff x=1$

Bảng biến thiên:

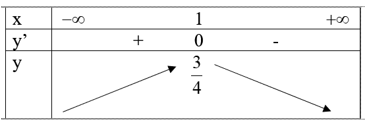
Từ bảng biến thiên ta có hàm số luôn đồng biến trên trên $\left(-\infty ;1\right)$.

Câu 6: Tìm tất cả các giá trị của tham số m để hàm số $y=\ln \left(16x^2+1\right)-\left(m+1\right)x+m+2$ nghịch biến trên khoảng $\left(-\infty ;\infty \right)$.

A. $m\in \left(-\infty ;-3\right]$

B. $m\in \left[3;+\infty \right)$

C. $m\in \left(-\infty ;-3\right)$

D. $m\in \left[-3;3\right]$

Lời giải

Chọn B

Ta có:

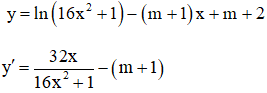
Hàm số nghịch biến trên R khi và chỉ khi $y^{\text{'}}\le 0$, $\forall x\in ℝ$

$\iff \frac{32x}{16x^2+1}-\left(m+1\right)\le 0$,

.$\forall x\in ℝ$

Cách 1:

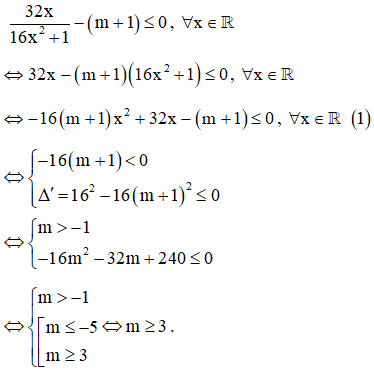
TH: $m=-1$ thì (1) thành $x\le 0$ nên $m=-1$ không thỏa mãn

Cách 2: ,

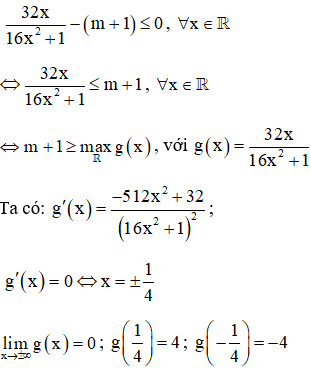
Bảng biến thiên:

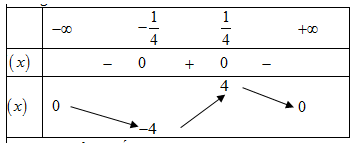
Dựa vào bảng biến thiên ta có $\underset{ℝ}{\max }g\left(x\right)=4$

Do đó:

$m+1\ge 4\iff m\ge 3$

III. BÀI TẬP TỰ LUYỆN

Câu 1: Tập xác định D của hàm số $y={\left(x^2-3x+2\right)}^{\sqrt{2}}$ là

A. $D=ℝ\backslash \left\{1;2\right\}$

B. $D=\left(-\infty ;-1\right)\cup \left(-2;+\infty \right)$

C. $D=\left(-\infty ;1\right)\cup \left(2;+\infty \right)$

D. $D=ℝ\backslash \left\{-1;2\right\}$

Câu 2: Hàm số $y=\left(x^2-2x+2\right){\text{e}}^x$ có đạo hàm là

A. $\left(2x+2\right){\text{e}}^x$

B. $x^2{\text{e}}^x$

C. $-2x{\text{e}}^x$

D. $\left(2x-2\right){\text{e}}^x$

Câu 3: Tính đạo hàm của hàm số $y=2^{\sqrt{1-x}}$.

A. $y^{\text{'}}=\frac{-\ln 2}{2\sqrt{1-x}}{.2}^{\sqrt{1-x}}$

B. $y^{\text{'}}=\frac{\ln 2}{2\sqrt{1-x}}{.2}^{\sqrt{1-x}}$

C. $y^{\text{'}}=\frac{-2^{\sqrt{1-x}}}{2\sqrt{1-x}}$

D. $y^{\text{'}}=\frac{2^{\sqrt{1-x}}}{2\sqrt{1-x}}$ .

Câu 4: Đạo hàm của hàm số $y=(2x^2-5x+2){\text{e}}^{\text{x}}$ là:

A. $x{\text{e}}^{\text{x}}$

B. $\left(2x^2-x-3\right){\text{e}}^{\text{x}}$

C. $2x^2{\text{e}}^{\text{x}}$

D. $\left(4x-5\right){\text{e}}^{\text{x}}$ .

Câu 5: Tập xác định D của hàm số $y={\log }_3\left({\log }_{2}x\right)$ là

A. $D=ℝ$

B. $D=\left(0;1\right)$

C. $D=\left(0;+\infty \right)$

D. $D=\left(1;+\infty \right)$ .

Câu 6: Cho hàm số $y={\log }_2{x}^2$. Tìm khẳng định sai.

A. Hàm số đồng biến trên $\left(0;+\infty \right)$.

B. Hàm số nghịch biến trên $\left(-\infty ;0\right)$.

C. Hàm số có một điểm cực tiểu.

D. Đồ thị hàm số có đường tiệm cận.

Câu 7: Cho ba số a, b, c dương và khác 1. Các hàm số $y={\log }_{a}x$, $y={\log }_{b}x$, $y={\log }_{c}x$ có đồ thị như hình vẽ sau

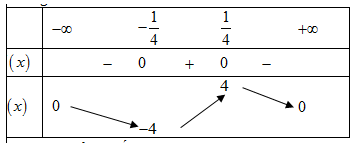
Khẳng định nào dưới đây đúng?

A. $a>c>b$

B. $a>b>c$ .

C. $c>b>a$

D. $b>c>a$ .

Câu 8: Tập xác định $y=\sqrt{-2x^2+5x-2}+\ln \frac{1}{x^2-1}$ là:

A. $D=\left(1;2\right]$

B. $D=\left[1;2\right]$

C. $D=\left(-1;1\right)$

D. $D=\left(-1;2\right)$

Câu 9: Tìm tập xác định của hàm số $y={\log }_3\frac{10-x}{x^2-3x+2}$.

A. $D=\left(-\infty ;1\right)\cup \left(2;10\right)$

B. $D=\left(1;+\infty \right)$

C. $D=\left(-\infty ;10\right)$

D. $D=\left(2;10\right)$

Câu 10: Đạo hàm của hàm số $y={\log }_8\left(x^2-3x-4\right)$ là:

A. $\frac{2x-3}{\left(x^2-3x-4\right)\ln 8}$

B. $\frac{2x-3}{\left(x^2-3x-4\right)\ln 2}$

C. $\frac{2x-3}{\left(x^2-3x-4\right)}$

D. $\frac{1}{\left(x^2-3x-4\right)\ln 8}$

Câu 11: Đạo hàm của hàm số $y=\log \left(2\sin x-1\right)$ trên tập xác định là:

A. $y^{\text{'}}=\frac{-2\cos x}{2\sin x-1}.$

B. $y^{\text{'}}=\frac{2\cos x}{2\sin x-1}.$

C. $y^{\text{'}}=\frac{2\cos x}{\left(2\sin x-1\right)\ln 10}.$

D. $y^{\text{'}}=\frac{-2\cos x}{\left(2\sin x-1\right)\ln 10}.$

Câu 12: Tính đạo hàm của hàm số $y=\ln \left(1+\sqrt{x+1}\right)$.

A. $y^{\text{'}}=\frac{1}{2\sqrt{x+1}\left(1+\sqrt{x+1}\right)}$

B. $y^{\text{'}}=\frac{1}{1+\sqrt{x+1}}$ .

C. $y^{\text{'}}=\frac{1}{\sqrt{x+1}\left(1+\sqrt{x+1}\right)}$

D. $y^{\text{'}}=\frac{2}{\sqrt{x+1}\left(1+\sqrt{x+1}\right)}$ .

Bảng đáp án bài tập tự luyện