100 công thức tính cực trị của đồ thị hàm số chi tiết nhất (2024 )

Công thức tính cực trị của hàm số chi tiết nhất 

1. Lý thuyết

Định nghĩa: Cho hàm số $y=f\left(x\right)$ xác định và liên tục trên khoảng $\left(a;b\right)$ (có thể a là $-\infty$; b là $+\infty$) và điểm $x_0\in \left(a;b\right)$

a. Nếu tồn tại số $h>0$ sao cho $f\left(x\right)>f\left(x_0\right)$ $\forall x\in \left(x_0-h;x_0+h\right)$ và $x\ne x_0$ thì ta nói hàm số $f\left(x\right)$ đạt cực tiểu tại $x_0$.

b. Nếu tồn tại số $h>0$ sao cho $f\left(x\right)<f\left(x_0\right)$ $\forall x\in \left(x_0-h;x_0+h\right)$ và $x\ne x_0$ thì ta nói hàm số $f\left(x\right)$ đạt cực đại tại $x_0$.

 Chú ý:

1. Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn được gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

2. Nếu hàm số f (x) đạt cực đại (cực tiểu) tại $x_0$ thì $x_0$ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; $f\left(x_0\right)$ được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số. Kí hiệu là $f_{CĐ}\left(f_{CT\text{}}\right)$, còn điểm $M\left(x_0;f\left(x_0\right)\right)$ được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

3. Dễ dàng chứng minh được rằng, nếu hàm số $y=f\left(x\right)$ có đạo hàm trên khoảng (a,b) và đạt cực đại hoặc cực tiểu tại $x_0$ thì $f\text{'}\left(x_0\right)=0$.

Thật vậy giả sử $f\left(x\right)$ đạt cực đại tại $x_0$. Khi đó theo định nghĩa ta có:

$\underset{\Delta x\to 0}{\lim }\frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}=0$

+ TH1: $\Delta x<0\Rightarrow f\text{'}\left({x_0}^{-}\right)=0$

+ TH2: $\Delta x>0\Rightarrow f\text{'}\left({x_0}^{+}\right)=0$

Mà $f\left(x\right)$ có đạo hàm nên suy ra $f\text{'}\left(x\right)=0$.

2. Điều kiện cần và điều kiện đủ để hàm số có cực trị

a. Điều kiện cần

- f (x) đạt cực trị tại $x_0$, có đạo hàm tại $x_0$ thì $f\text{'}\left(x_0\right)=0$.

b. Điều kiện đủ

- Định lí 1: Giả sử hàm số $y=f\left(x\right)$ liên tục trên khoảng $K=\left(x_0-h;x_0+h\right)$ và có đạo hàm trên K hoặc trên $K\text{}\left\{x_0\right\}$ với $h>0$

+ Nếu $f\text{'}\left(x\right)>0$ trên khoảng $\left(x_0-h;x_0\right)$ và $f\text{'}\left(x\right)<0$ trên khoảng $\left(x_0;x_0+h\right)$ thì $x_0$ là một điểm cực đại của hàm số $f\left(x\right)$.

+ Nếu $f\text{'}\left(x\right)<0$ trên khoảng $\left(x_0-h;x_0\right)$ và $f\text{'}\left(x\right)>0$ trên khoảng $\left(x_0;x_0+h\right)$ thì $x_0$ là một điểm cực tiểu của hàm số $f\left(x\right)$.

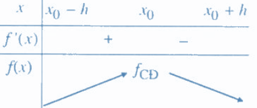
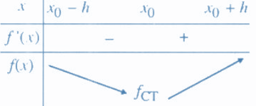
- Nói một cách dễ hiểu thì: Đi từ trái qua phải:

+ Nếu $f\text{'}\left(x\right)$ đổi dấu từ + sang - khi đi qua $x_0$ thì $x_0$ là điểm cực đại

+ Nếu $f\text{'}\left(x\right)$ đổi dấu từ - sang + khi đi qua $x_0$ thì $x_0$ là điểm cực tiểu.

- Tóm lại muốn hàm số có cực trị tại $x_0$ thì $f\text{'}\left(x\right)$ phải đổi dấu khi qua $x_0$

- Định lí 2: Giả sử hàm số $y=f\left(x\right)$ có đạo hàm cấp 2 trong khoảng $\left(x_0-h;x_0+h\right)$, với $h>0$. Khi đó:

+) Nếu $\left\{\begin{array}{l}f\text{'}\left(x_0\right)=0\\ f\text{'}\text{'}\left(x_0\right)<0\end{array}\right.$ thì $x_0$ là điểm cực đại;

+) Nếu $\left\{\begin{array}{l}f\text{'}\left(x_0\right)=0\\ f\text{'}\text{'}\left(x_0\right)>0\end{array}\right.$ thì $x_0$ là điểm cực tiểu.

3. Quy tắc tìm cực trị

a. Quy tắc 1. (Dựa vào định lí 1)

+B1: Tìm tập xác định

+B2: Tính $f\text{'}\left(x\right)$. Tìm các điểm tại đó $f\text{'}\left(x\right)=0$ hoặc $f\text{'}\left(x\right)$ không xác định.

+B3: Lập bảng xét dấu $f\text{'}\left(x\right)$

+B4: Từ bảng xét dấu suy ra các điểm cực trị.

b. Quy tắc 2 (Dựa vào định lí 2)

+B1: Tìm tập xác định

+B2: Tính $f\text{'}\left(x\right)$ và giải phương trình $f\text{'}\left(x\right)=0$được nghiệm $x_i$

+B3: Tính $f\text{'}\text{'}\left(x\right)$ và $f\text{'}\text{'}\left(x_i\right)$ suy ra tính chất cực trị của các điểm $x_i$ rồi kết luận.

Chú ý: Nếu $f\text{'}\text{'}\left(x_i\right)=0$ thì ta phải dùng quy tắc 1 để xét cực trị.

Lưu ý: Hàm trùng phương  $y=a{x}^4+b{x}^2+c$

+) Có 1 cực trị khi $a.b\ge 0$

+) Có 3 cực trị khi $a.b<0$

4. Một số ví dụ

Ví dụ 1: Tìm các điểm cực trị của hàm số

a) $y=x^3-3x^2-9x+2$

b) $y=x^4-2x^2+2$

Lời giải

a) TXĐ: $D=ℝ$

Ta có:

$$\begin{gathered} y\text{'}=0\iff 3x^2-6x-9=0 \\ \iff \left[\begin{array}{l}x=3\\ x=-1\end{array}\right. \end{gathered}$$

Bảng biến thiên (xét dấu):

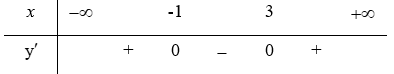
Từ bảng xét dấu ta thấy hàm số đạt cực đại tại điểm $x=-1$

Hàm số đạt cực tiểu tại điểm x = 3

b) TXĐ: $D=ℝ$

Ta có: $y^{\text{'}}=4x^3-4x$;

$$\begin{gathered} y\text{'}\text{'}=12x^2-4 \\ y\text{'}=0\iff \left\{\begin{array}{l}x=0\\ x=\pm 1\end{array}\right. \end{gathered}$$

Ta có: $y\text{'}\text{'}\left(0\right)=-4<0\Rightarrow x=0$  là điểm cực đại

$y\text{'}\text{'}\left(1\right)=y\text{'}\text{'}\left(-1\right)=8>0$

$\Rightarrow x=1$ và $x=-1$ là hai điểm cực tiểu của hàm số.

Ví dụ 2: Tìm m để hàm số

a) $y=x^3-2m{x}^2+m^{2}x-1$ đạt cực đại tại x=1.              

b) $y=\frac{x^2-mx+2}{x-1}$ đạt cực tiểu tại $x=2$.

Lời giải

a) TXĐ: $D=ℝ$.

Ta có: $y^{\text{'}}=3x^2-4mx+m^2$;

$y\text{'}\text{'}=6x-4m$

Hàm số đạt cực đại tại:

$$\begin{gathered} x=1\iff \left\{\begin{array}{l}y\text{'}\left(1\right)=0\\ y\text{'}\text{'}\left(1\right)<0\end{array}\right. \\ \iff \left\{\begin{array}{l}{m}^2-4m+3=0\\ 6-4m<0\end{array}\right. \\ \iff \left\{\begin{array}{l}\left[\begin{array}{l}m=1\\ m=3\end{array}\right.\\ m>\frac{3}{2}\end{array}\right.\iff m=3 \end{gathered}$$

Vậy m =3.

b. TXĐ: $D=ℝ\text{}\left\{1\right\}$.

Ta có:

$$\begin{gathered} y\text{'}=\frac{x^2-2x+m-2}{{\left(x-1\right)}^2} \\ =1+\frac{m-3}{{\left(x-1\right)}^2} \\ \Rightarrow y\text{'}\text{'}=-\frac{2\left(m-3\right)}{{\left(x-1\right)}^3} \end{gathered}$$

Hàm số đạt cực tiểu tại:

$$\begin{gathered} x=2\iff \left\{\begin{array}{l}y\text{'}\left(2\right)=0\\ y\text{'}\text{'}\left(2\right)>0\end{array}\right. \\ \iff \left\{\begin{array}{l}m-2=0\\ -2\left(m-3\right)>0\end{array}\right. \\ \iff m=2 \end{gathered}$$

Vậy m=2.

- Lưu ý: Trong một vài bài toán tính đạo hàm cấp 2 phức tạp ta có thể thay giá trị của m tìm được vào hàm số và sử dụng công cụ $\frac{d}{dx}$ của MTCT để xác định dấu của $y\text{'}\text{'}$ một cách nhanh chóng.      

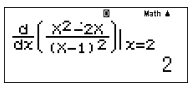
Kết quả là 2 > 0 nên m=2(t/m)

5. Luyện tập

Bài 1. Áp dụng quy tắc I, hãy tìm các điểm cực trị của các hàm số sau:

a. $x^3-6x^2+9x-2$

b. $x^4+2x^2-2$

c. $y=\frac{x^2+2x+1}{x+2}$

Bài 2. Tìm m để hàm số:

a. $y=m{x}^4+\left(m-2\right)x^2+3$ có 3 điểm cực trị

b. $y=\frac{1}{3}{x}^3-2m{x}^2+3m^{2}x-3$ đạt cực đại tại $x=2$

Bài 3. Áp dụng quy tắc II, hãy tìm các điểm cực trị của các hàm số sau:

a. $y=x^4-4x^2+1$

b.  $y=-\frac{1}{3}{x}^3+2x^2+5x-2$

c. $y=\sin x+\cos x$

Bài 4. Tìm m để hàm số $y=\frac{1}{3}{x}^3+m{x}^2+\left(4m-3\right)x+2$ có hai điểm cực trị nằm về hai phía so với trục tung.