100 bài tập về phương pháp vẽ đồ thị Parabol (2024 có đáp án) và cách giải các dạng toán

Phương pháp vẽ đồ thị Parabol chi tiết nhất

I. Lí thuyết tổng hợp

- Tập xác định của phương trình Parabol: D=R𝐷=ℝ

- Trục đối xứng của Parabol: là đường thẳng đi qua đỉnh của Parabol và song song với trục Oy có phương trình x=−b2a𝑥=−𝑏2𝑎

- Đồ thị Parabol có hai dạng:

+) Dạng 1: a > 0 (bề lõm của đồ thị hướng lên trên)

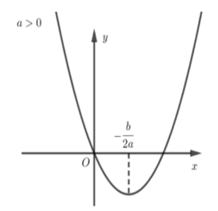
Hàm số y=ax2+bx+c𝑦=𝑎𝑥2+𝑏𝑥+𝑐 đồng biến trên khoảng (−b2a;+∞)−𝑏2𝑎;+∞ và nghịch biến trên khoảng (−∞;−b2a)−∞;−𝑏2𝑎.

+) Dạng 2: a < 0 (bề lõm của đồ thị hướng xuống dưới)

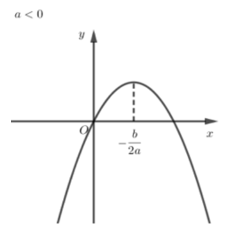
Hàm số y=ax2+bx+c𝑦=𝑎𝑥2+𝑏𝑥+𝑐 nghịch biến trên khoảng (−b2a;+∞)−𝑏2𝑎;+∞ và đồng biến trên khoảng (−∞;−b2a)−∞;−𝑏2𝑎.

II. Các công thức

Cách vẽ đồ thị Parabol: y=ax2+bx+c𝑦=𝑎𝑥2+𝑏𝑥+𝑐

Bước 1: Vẽ trục đối xứng có phương trình x=−b2a𝑥=−𝑏2𝑎.

Bước 2: Xác định tọa độ đỉnh : I(−b2a;−Δ4a)𝐼−𝑏2𝑎;−𝛥4𝑎.

Bước 3: Xác định thêm 1 số điểm (tối thiểu 1 điểm) như giao điểm với trục tung M (0; c) (nếu có), trục hoành (nếu có) hoặc các điểm tùy ý. Sau đó lấy điểm đối xứng với các điểm điểm đó qua trục đối xứng.

Bước 4: Vẽ đồ thị bằng cách nối các điểm lại theo dạng hình Parabol.

Lưu ý: a > 0 và a < 0 cho ra hai dạng đồ thị Parabol khác nhau.

III. Ví dụ minh họa

Bài 1: Vẽ đồ thị Parabol:y=x2−4x+4𝑦=𝑥2−4𝑥+4 . Xét tính đồng biến, nghịch biến của nó trên tập xác định.

Lời giải:

- Tập xác định: D=R𝐷=ℝ

- Ta có trục đối xứng của đồ thị: x=−(−4)2.1=2𝑥=−(−4)2.1=2

- Xét Δ=(−4)2−4.1.4=0⇒𝛥=(−4)2−4.1.4=0⇒ Tọa độ đỉnh I của Parabol:

xI=−(−4)2.1=2yI=04.1=0𝑥𝐼=−(−4)2.1=2𝑦𝐼=04.1=0

⇒⇒ I (2; 0)

- Giao điểm của Parabol với trục tung: C(0; 4). Lấy thêm điểm C’(4; 4) đối xứng với C qua trục đối xứng.

- Có a = 1 > 0 , trục đối xứng x = 2 và các điểm I (2; 0) , C (0; 4), C’(4; 4) ta vẽ được đồ thị:

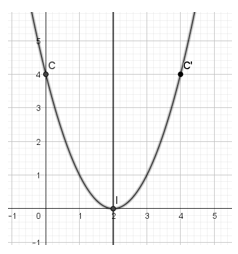
- Dựa vào đồ thị ta có thể thấy, hàm số y=x2−4x+4𝑦=𝑥2−4𝑥+4 đồng biến trên khoảng (2;+∞)(2;+∞) và nghịch biến trên khoảng (−∞;2)(−∞;2).

Bài 2: Vẽ đồ thị Parabol: y=x2−4x+5𝑦=𝑥2−4𝑥+5.

Lời giải:

- Tập xác định: D=R𝐷=ℝ

- Ta có trục đối xứng của đồ thị: x=−(−4)2.1=2𝑥=−(−4)2.1=2

- Xét Δ=(−4)2−4.1.5=−4𝛥=(−4)2−4.1.5=−4 Tọa độ đỉnh I của Parabol:

xI=−(−4)2.1=2yI=−(−4)4.1=1𝑥𝐼=−(−4)2.1=2𝑦𝐼=−(−4)4.1=1

⇒⇒ I (2; 1)

- Giao điểm của Parabol với trục tung: A (0; 5). Lấy thêm điểm A’(4; 5) đối xứng với A qua trục đối xứng.

- Có a = 1 > 0 , trục đối xứng x = 2 và các điểm I (2; 1), A (0; 5), A’(4; 5) ta vẽ được đồ thị:

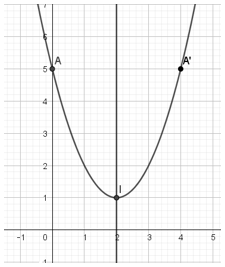
Bài 3: Vẽ đồ thị Parabol:y=−x2−3x+4𝑦=−𝑥2−3𝑥+4

Lời giải:

- Tập xác định: D=R𝐷=ℝ

- Ta có trục đối xứng của đồ thị:x=−(−3)2.(−1)=−32𝑥=−(−3)2.(−1)=−32

- Xét Δ=(−3)2−4.(−1).4=25⇒𝛥=(−3)2−4.(−1).4=25⇒ Tọa độ đỉnh I của Parabol:

xI=−(−3)2.(−1)=−32yI=−254.(−1)=254𝑥𝐼=−(−3)2.(−1)=−32𝑦𝐼=−254.(−1)=254

⇒⇒ I(−32;254)−32;254

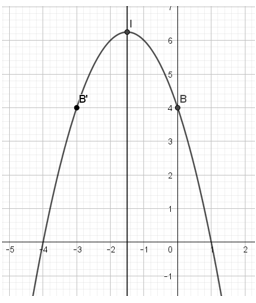
- Giao điểm của Parabol với trục tung: B (0; 4). Lấy thêm điểm B’(-3; 4) đối xứng với B qua trục đối xứng.

- Có a = -1 < 0 , trục đối xứng x=−32𝑥=−32 và các điểm I(−32;254)−32;254 , B (0; 4), B’(-3; 4) ta vẽ được đồ thị:

IV. Bài tập tự luyện

Bài 1: Vẽ đồ thị Parabol:y=2x2−7x+10𝑦=2𝑥2−7𝑥+10. Và xét tính đồng biến, nghịch biến của nó trên tập xác định.

Bài 2: Vẽ đồ thị Parabol: y=−3x2−5x+3𝑦=−3𝑥2−5𝑥+3. Và xét tính đồng biến, nghịch biến của nó trên tập xác định.