100 bài tập về Tiệm cận của đồ thị hàm số (có đáp án 2024)

Tiệm cận của đồ thị hàm số và cách giải bài tập

A. LÝ THUYẾT.

1. Đường tiệm cận đứng.

Cho hàm số y = f(x) xác định trên một khoảng vô hạn (là khoảng dạng $\left(a;+\infty \right)$; $\left(-\infty ;b\right)$ hoặc $\left(-\infty ;+\infty \right)$).

- Định nghĩa: Đường thẳng $x=x_0$ được gọi là đường tiệm cận đứng của đồ thị hàm số nếu ít nhất một trong các điều kiện sau đây được thỏa mãn:

$\underset{x\to {x_0}^{+}}{\lim }f\left(x\right)=+\infty$;$\underset{x\to {x_0}^{+}}{\lim }f\left(x\right)=-\infty$;

$\underset{x\to {x_0}^{-}}{\lim }f\left(x\right)=+\infty$;$\underset{x\to {x_0}^{-}}{\lim }f\left(x\right)=-\infty$.

2. Đường tiệm cận ngang.

- Định nghĩa: Đường thẳng $y=y_0$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y=f\left(x\right)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn: $\underset{x\to +\infty }{\lim }f\left(x\right)=y_0$;$\underset{x\to -\infty }{\lim }f\left(x\right)=y_0$

Chú ý:

- Đồ thị hàm số $y=\frac{ax+b}{cx+d},\left(ad-bc\ne 0,c\ne 0\right)$ luôn có tiệm cận ngang và tiệm cận đứng lần lượt là $y=\frac{a}{c}$; $x=-\frac{d}{c}$.

- Nếu $y=f\left(x\right)=\frac{P\left(x\right)}{Q\left(x\right)}$ là hàm số phân thức hữu tỉ.

+ Nếu Q(x) = 0 có nghiệm là x0, và x0 không là nghiệm của P(x) = 0 thì đồ thị có tiệm cận đứng là .

+ Nếu bậc (P(x)) $\le$bậc (Q(x)) thì đồ thị hàm số có tiệm cận ngang.

B. CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Xác định tiệm cận của hàm số.

1. Phương pháp giải.

Dựa vào định nghĩa để giải bài toán.

2. Ví dụ minh hoạ.

Ví dụ 1. Chọn khẳng định đúng trong các khẳng định sau:

A. Đồ thị hàm số $y=f\left(x\right)$ có tiệm cận ngang $y=1$ khi và chỉ khi $\underset{x\to +\infty }{\lim }f\left(x\right)=1$ và $\underset{x\to -\infty }{\lim }f\left(x\right)=1$.

B. Nếu hàm số $y=f\left(x\right)$ không xác định tại $x_0$ thì đồ thị hàm số $y=f\left(x\right)$ có tiệm cận đứng $x=x_0$.

C. Đồ thị hàm số $y=f\left(x\right)$ có tiệm cận đứng $x=2$ khi và chỉ khi $\underset{x\to 2^{+}}{\lim }f\left(x\right)=+\infty$ và $\underset{x\to 2^{-}}{\lim }f\left(x\right)=+\infty$.

D. Đồ thị hàm số $y=f\left(x\right)$ bất kì có nhiều nhất hai đường tiệm cận ngang.

Lời giải

A sai vì chỉ cần một trong hai giới hạn $\underset{x\to -\infty }{\lim }f\left(x\right)=1$ hoặc $\underset{x\to +\infty }{\lim }f\left(x\right)=1$ tồn tại thì đã suy ra được tiệm cận ngang là $y=1$.

B sai, ví dụ hàm số $y=\sqrt{x^3-1}$ không xác định tại $x=-2$ nhưng $\underset{x\to {\left(-2\right)}^{-}}{\lim }f\left(x\right)$ và $\underset{x\to {\left(-2\right)}^{+}}{\lim }f\left(x\right)$ không tiến đến vô cùng nên $x=-2$ không phải là tiệm cận đứng của đồ thị hàm số.

C sai vì chỉ cần tồn tại một trong bốn giới hạn sau:

$$\begin{gathered} \underset{x\to 2^{-}}{\lim }f\left(x\right)=-\infty ,\underset{x\to 2^{-}}{\lim }f\left(x\right)=+\infty , \\ \underset{x\to 2^{+}}{\lim }f\left(x\right)=-\infty ,\underset{x\to 2^{+}}{\lim }f\left(x\right)=+\infty \end{gathered}$$

D đúng vì chỉ có hai giới hạn $\underset{x\to -\infty }{\lim }f\left(x\right),\underset{x\to +\infty }{\lim }f\left(x\right)$.

Chọn D.

Ví dụ 2. Tiệm cận đứng của đồ thị hàm số $y=\frac{x+1}{x-2}$ là đường thẳng có phương trình:

A. $x=-1$

B. $x=-2$

C. $x=2$

D. $x=1$

Lời giải

Ta có: $\underset{x\to 2^{+}}{\lim }y=\underset{x\to 2^{+}}{\lim }\frac{x+1}{x-2}=+\infty$.

(hoặc $\left.\underset{x\to 2^{-}}{\lim }y=\underset{x\to 2^{-}}{\lim }\frac{x+1}{x-2}=-\infty \right)$.

Vậy $x=2$ là tiệm cận đứng của đồ thị hàm số.

Chọn C.

Ví dụ 3. Cho hàm số xác định và liên tục trên có bảng biến thiên như sau:

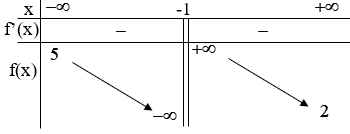
Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số có một đường tiệm cận.

B. Đồ thị hàm số có hai đường tiệm cận.

C. Đồ thị hàm số có hai TCN và một TCĐ

D. Đồ thị hàm số có bốn đường tiệm cận.

Lời giải

Từ bảng biến thiên, ta có:

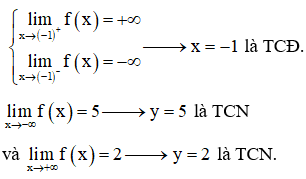
Chọn C.

3. Bài tập vận dụng.

Câu 1. Tiệm cận đứng của đồ thị hàm số $y=\frac{2x-2}{x+1}$ là

A. $x=-2$

B. $x=1$

C. $x=-1$

D. $x=2$

Câu 2. Tiệm cận ngang của đồ thị hàm số $y=\frac{4x+1}{x-1}$ là

A. $y=\frac{1}{4}$

B. $y=4$

C. $y=1$

D. $y=-1$

Câu 3. Tiệm cận ngang của đồ thị hàm số $y=\frac{5x+1}{x-1}$ là:

A. $y=1$

B. $y=\frac{1}{5}.$

C. $y=-1$

D. $y=5.$

Câu 4. Cho hàm số $y=f\left(x\right)$ có $\underset{x\to +\infty }{\lim }f\left(x\right)=1$ và $\underset{x\to -\infty }{\lim }f\left(x\right)=-1$. Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số có đúng một tiệm cận ngang.

C. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng $y=1$ và $y=-1$.

D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng $x=1$ và $x=-1$.

Câu 5. Cho hàm số $y=f\left(x\right)$ có $\underset{x\to +\infty }{\lim }f\left(x\right)=0$ và $\underset{x\to -\infty }{\lim }f\left(x\right)=+\infty$. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số nằm phía trên trục hoành.

C. Đồ thị hàm số có một tiệm cận ngang là trục hoành.

D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng $y=0.$

Câu 6. Cho hàm số $y=f\left(x\right)$ có $\underset{x\to +\infty }{\lim }f\left(x\right)=0$ và $\underset{x\to 0^{+}}{\lim }f\left(x\right)=+\infty$. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận đứng.

B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho.

C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng $y=0$.

D. Hàm số đã cho có tập xác định là $\text{D}=\left(0,+\infty \right)$.

Câu 7. Cho hàm số $y=f\left(x\right)$ xác định và liên tục trên $ℝ\backslash \left\{-1\right\}$, có bảng biến thiên như sau:

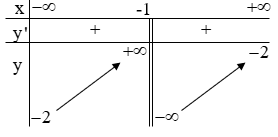
Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số có tiệm cận đứng $y=-1$ và tiệm cận ngang $x=-2.$

B. Đồ thị hàm số có duy nhất một tiệm cận.

C. Đồ thị hàm số có ba tiệm cận.

D. Đồ thị hàm số có tiệm cận đứng $x=-1$ và tiệm cận ngang $y=-2.$

Câu 8. Cho hàm số $f\left(x\right)$ xác định và liên tục trên $ℝ\backslash \left\{-1\right\},$ có bảng biến thiên như sau:

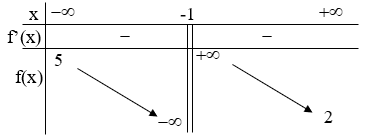
Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số có một đường tiệm cận.

B. Đồ thị hàm số có hai đường tiệm cận.

C. Đồ thị hàm số có hai TCN $y=2,y=5$ và một TCĐ $x=-1.$

D. Đồ thị hàm số có bốn đường tiệm cận.

Câu 9. Cho hàm số $y=f\left(x\right)$ xác định trên $ℝ\backslash \left\{0\right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

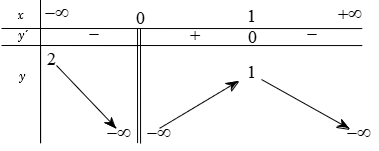
Mệnh đề nào sau đây là đúng?

A. Đồ thị hàm số có một đường tiệm cận đứng.

B. Hàm số đạt cực tiểu tại $x=0.$

C. Giá trị lớn nhất của hàm số là 1

D. Hàm số không có cực trị.

Câu 10. Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như sau:

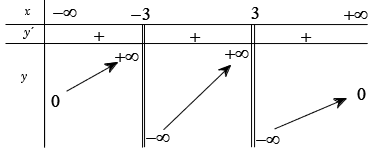
Mệnh đề nào sau đây là sai?

A. Đồ thị hàm số có tiệm cận đứng là $x=-3.$

B. Đồ thị hàm số có tiệm cận đứng là $x=3.$

C. Đồ thị hàm số có tiệm cận ngang là $y=0.$

D. Đồ thị hàm số có tất cả hai đường tiệm cận.

Câu 11. Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như sau:

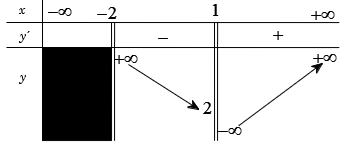
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 3

D. 4

Câu 12. Tìm số tiệm cận đứng của đồ thị hàm số $y=\frac{x^2-3x-4}{x^2-16}$.

A. 2.

B. 3

C. 0.

D. 1.

Câu 13. Đồ thị hàm số nào trong các hàm số dưới đây có tiệm cận đứng?

A. $y=\frac{1}{\sqrt{x}}.$

B. $y=\frac{1}{x^4+1}.$

C. $y=\frac{1}{x^2+1}.$

D. $y=\frac{1}{x^2+x+1}.$

Câu 14. Đồ thị hàm số $y=\left\{\begin{array}{ll}\frac{\sqrt{x^2+1}}{x}& \text{khi }x\ge 1\\ \frac{2x}{x-1}& \text{khi }x<1\end{array}\right.$ có tất cả bao nhiêu đường tiệm cận?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 15. Đồ thị hàm số nào sau đây có đúng hai tiệm cận ngang?

A. $y=\frac{\sqrt{x^2-x}}{\left|x\right|+2}$.

B. $y=\frac{\left|x\right|-2}{x+1}$.

C. $y=\frac{\sqrt{4-x^2}}{x+1}$.

D. $y=\frac{\sqrt{x+2}}{\left|x\right|-2}$.

Câu 16. Đồ thị hàm số $y=\frac{x+1}{\sqrt{4x^2+2x+1}}$ có tất cả bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 3

D. 4

Câu 17. Đồ thị hàm số $y=\frac{\sqrt{x-7}}{x^2+3x-4}$ có bao nhiêu đường tiệm cận đứng?

A. 1.

B. 2.

C. 0.

D. 3.

Câu 18. Gọi n,d lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số $y=\frac{\sqrt{1-x}}{\left(x-1\right)\sqrt{x}}.$ Khẳng định nào sau đây là đúng?

A. $n=d=1.$

B. $n=0;d=1.$

C. $n=1;d=2.$

D. $n=0;d=2.$

Câu 19. Đồ thị hàm số $y=\frac{\sqrt{16-x^2}}{x^2-16}$ có tất cả bao nhiêu đường tiệm cận?

A. 0

B. 1

C. 2

D. 3

Câu 20. Cho hàm số $y=\frac{x-1}{\sqrt{2x^2-1}-1}$. Gọi d,n lần lượt là số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số. Mệnh đề nào sau đây là đúng?

A. $n+d=1.$

B. $n+d=2.$

C. $n+d=3$

D. $n+d=4$

Câu 21. Tìm số tiệm cận đứng của đồ thị hàm số $y=\frac{x^2-3x-4}{x^2-16}$.

A. 2.

B. 3.

C. 1

D. 0.

Câu 22. Cho đường cong $\left(C\right):y=\frac{x-2}{x+2}$. Điểm nào dưới đây là giao của hai tiệm cận của (C)?

A. $L\left(-2;2\right)$

B. $M\left(2;1\right)$

C. $N\left(-2;-2\right)$

D. $K\left(-2;1\right)$

Câu 23. Đồ thị của hàm số nào dưới đây không có tiệm cận đứng ?

A. $y=\frac{1}{\sqrt{x+3}}$

B. $y=\frac{1}{2x^2+x+1}$

C. $y=\frac{1}{x^4-1}$

D. $y=\frac{1}{x^2-x-1}$

Câu 24. Đồ thị của hàm số $y=\frac{x-2}{x^2-4}$ có bao nhiêu tiệm cận ?

A. 0

B. 3

C. 1

D. 2

Câu 25. Tổng số các đường tiệm cận đứng và tiệm cận ngang của hai đồ thị hàm số $y=\frac{2\text{x}-1-\sqrt{x^2+x+3}}{x^2-5x+6}$ và $y=\frac{x^2-3\text{x}-4}{x^2-1}$ là

A. 5.

B. 3

C. 2.

D. 4.

Câu 26. Các đường tiệm cận của đồ thị hàm số $y=\frac{4x+3}{x-2}$ tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

A. 3

B. 12

C. 8

D. 6

Câu 27. Cho hàm số $y=\frac{x+5+\sqrt{2-x}}{\sqrt{x^2-3x+2}}$. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số có một đường tiệm cận ngang là đường thẳng $y=1$.

B. Đồ thị hàm số có một đường tiệm cận ngang là đường thẳng $y=0$.

C. Đồ thị hàm số có một đường tiệm cận ngang là đường thẳng $y=-1$.

D. Đồ thị hàm số có hai đường tiệm cận ngang là hai đường thẳng $y=-1$ và $y=1$.

Câu 28. Tìm điểm M thuộc đồ thị hàm số sao cho khoảng cách từ M đến tiệm cận ngang bằng khoảng cách từ M đến trục tung.

A. $M\left(2;\frac{1}{3}\right)$

B. $M\left(2;1\right),M\left(4;3\right)$.

C. $M\left(1;0\right),M\left(-2;3\right)$

D. $M\left(0;1\right),M\left(-2;3\right)$.

Câu 29. Cho hàm số $y=\frac{2x-3}{x-2} \left(C\right)$. Gọi M là điểm bất kỳ trên (C), d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d là

A. 5

B. 10

C. 6

D. 2

Câu 30. Cho hàm số $y=\frac{1-3x}{3-x}$ có đồ thị (C). Điểm M nằm trên (C) sao cho khoảng cách từ M đến tiệm cận đứng gấp hai lần khoảng cách từ M đến tiệm cận ngang của (C) . Khoảng cách từ M đến giao điểm hai đường tiệm cận của (C) bằng

A. $3\sqrt{2}$

B. 4

C. 5

D. $2\sqrt{5}$

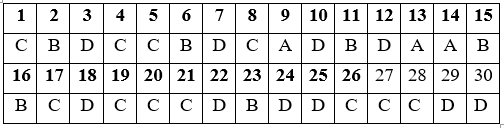
Đáp án

Dạng 2. Tìm m để hàm số có tiệm cận thoả mãn điều kiện cho trước.

1. Phương pháp giải.

Bước 1. Tìm điều kiện của tham số để hàm số xác định.

Bước 2. Tìm các đường tiệm cận của đồ thị hàm số.

Bước 3. Giải điều kiện của bài toán để tìm tham số.

Bước 4. Kết luận

Lưu ý:

Với Hàm số $y=\frac{ax+b}{cx+d}\left(ad-bc\ne 0,c\ne 0\right)$, ta có:

Gọi $M\left(x_0;y_0\right)$ là điểm thuộc đồ thị hàm số $y=\frac{ax+b}{cx+d}$, suy ra $M\left(x_0;y_0=\frac{a{x}_0+b}{c{x}_0+d}\right)$

Đồ thị hàm số $y=\frac{ax+b}{cx+d}$ có TCĐ ${\Delta }_1:x+\frac{d}{c}=0$ ; TCN ${\Delta }_2:y-\frac{a}{c}=0$.

Ta có :

$\left\{\begin{array}{l}{d}_1=d\left[M,{\Delta }_1\right]=\left|x_0+\frac{d}{c}\right|=\left|\frac{c{x}_0+d}{c}\right|\\ d_2=d\left[M,{\Delta }_2\right]=\left|y_0-\frac{a}{c}\right|=\left|\frac{ad-bc}{c\left(c{x}_0+d\right)}\right|\end{array}\right.$

2. Ví dụ minh hoạ.

Ví dụ 1. Tìm trên đồ thị hàm số $y=\frac{2x+1}{x-1}$ những điểm M sao cho khoảng cách từ M đến tiệm cận đứng bằng ba lần khoảng cách từ M đến tiệm cận ngang của đồ thị.

A. $M\left(-4;\frac{7}{5}\right)$ hoặc $M\left(2;5\right)$.

B. $M\left(4;3\right)$ hoặc $M\left(-2;1\right)$.

C. $M\left(4;3\right)$ hoặc $M\left(2;5\right)$.

D. $M\left(-4;\frac{7}{5}\right)$ hoặc $M\left(-2;1\right)$.

Lời giải

Gọi $M\left(a;\frac{2a+1}{a-1}\right)$ với $a\ne 1$ là điểm thuộc đồ thị.

Đường tiệm cận đứng $d:x=1;$ đường tiệm cận ngang $d^{\text{'}}:y=2$.

Yêu cầu bài toán

$$\begin{gathered} \iff d\left[M,d\right]=3d\left[M,d^{\text{'}}\right] \\ \iff \left|a-1\right|=3\left|\frac{2a+1}{a-1}-2\right| \\ \iff {\left(a-1\right)}^2=9\iff \left[\begin{array}{l}a=4\\ a=-2\end{array}\right. \\ \Rightarrow \left[\begin{array}{l}M\left(4;3\right)\\ M\left(-2;1\right)\end{array}\right. \end{gathered}$$

Chọn B.

Ví dụ 2. Tìm tất cả các giá trị thực của tham số sao cho đồ thị của hàm số $y=\frac{x+1}{\sqrt{m{x}^2+1}}$ có hai tiệm cận ngang.

A. Không có giá trị thực nào của thỏa mãn yêu cầu đề bài.

B. m <0

C. m = 0

D. m >0

Lời giải

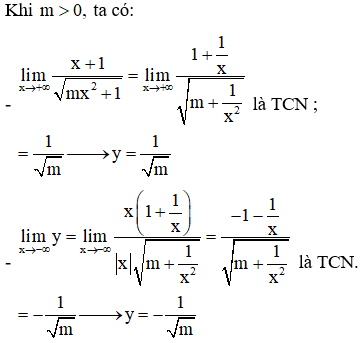
Với $m=0$ suy $y=\frac{x+1}{1}\stackrel{}{\to }$ đồ thị hàm số không có tiệm cận.

Với $m<0$ thì hàm số có TXĐ là một đoạn nên đồ thị hàm số không có TCN.

Vậy với $m>0$ thì đồ thị hàm số có hai tiệm cận ngang.

Chọn D.

Áp dụng công thức giải nhanh.

$$\begin{gathered} \left|\frac{c{x}_0+d}{c}\right|=k\left|\frac{ad-bc}{c\left(c{x}_0+d\right)}\right|\stackrel{}{\to }{x}_0 \\ =-\frac{d}{c}\pm \sqrt{kp} \end{gathered}$$

với $c=1,d=-1,k=3,$

$p=\left|\frac{ad-bc}{c^2}\right|=3$. Suy ra $x_0=1\pm 3$

3. Bài tập tự luyện.

Câu 1. Tìm tất cả các giá trị thực của tham số m để đường tiệm cận ngang của đồ thị hàm số $y=\frac{\left(m+2\right)x-3}{4-x}$ đi qua điểm $A\left(-1;2\right)$.

A. $m=-2$

B. $m=1$

C. $m=-4$

D. $m=2$

Câu 2. Tìm tất cả các giá trị thực của tham số m để đường tiệm cận đứng của đồ thị hàm số $y=\frac{4x-5}{x-m}$ đi qua điểm $A\left(-3;1\right)$.

A. $m=-3$

B. $m=-4$

C. $m=5$

D. $m=4$

Câu 3. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $\left[-2021;2021\right]$ để đồ thị hàm số $y=\frac{x+1}{x^2-mx+4}$ có 3 đường tiệm cận?

A. $4033$

B. $4034$

C. $2017$

D. $2016$

Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y=\frac{x+2}{x^3-3x^2+m}$ có nhiều đường tiệm cận nhất.

A. $m\in ℝ$.

B. $\left[\begin{array}{l}m>0\\ m<-4\end{array}\right.$.

C. $0<m<4$

D. $-4<m<0$

Câu 5. Số các giá trị của tham số m để đồ thị hàm số $y=\frac{x+m}{mx-2}$ có đúng 1 tiệm cận đứng và 1 tiệm cận ngang, đồng thời hai tiệm cận này tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 18 là

A. 0.

B. 1

C. 2.

D. 3.

Câu 6. Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hàm số $y=\frac{1+\sqrt{x+1}}{\sqrt{x^2-mx-3m}}$ có đúng hai tiệm cận đứng.

A. $\left(0;\frac{1}{2}\right]$

B. $\left(0;+\infty \right)$

C. $\left[\frac{1}{4};\frac{1}{2}\right]$

D. $\left(0;\frac{1}{2}\right)$.

Câu7. Có bao nhiêu giá trị thực của m để đồ thị hàm số $f\left(x\right)=\frac{m^{2}x-\sqrt{x^2+x+6}}{x-1}$ có tiệm cận ngang là đường thẳng $y=3$.

A. 1

B. 2

C. 4

D. Vô số.

Câu 8. Đồ thị của hàm số $y=\frac{a{x}^2+x-3}{4x^2+bx+1}$ có một đường tiệm cận ngang là $y=c$ và chỉ có một đường tiệm cận đứng. Tính $\frac{a}{bc}$ biết rằng a là số thực dương và $ab=4$?

A. $\frac{a}{bc}=\frac{1}{4}$

B. $\frac{a}{bc}=1$

C. $\frac{a}{bc}=4$

D. $\frac{a}{bc}=2$

Câu 9. Có bao nhiêu giá trị nguyên của tham số $a\in \left[-2021;2021\right]$ để đồ thị hàm số $y=\frac{x-\sqrt{x^2+1}}{\sqrt{a{x}^2+2}}$ có tiệm cận ngang?

A. 2022.

B. 2021.

C. 4042.

D. 2020.

Câu 10. Cho hàm số $y=\frac{2x-2}{x-2}$ có đồ thị là (C), M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A,B thỏa mãn $AB=2\sqrt{5}$. Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Tìm giá trị của S.

A. 8

B. 9

C. 5

D. 6

Câu 11. Nếu đồ thị $y=\frac{m{x}^2+\left(3-m\right)x-2}{x-1}$ có đường tiệm cận xiên tiếp xúc với đường tròn có phương trình ${\left(x-1\right)}^2+{\left(y-4\right)}^2=2$ thì tập tất cả các giá trị của m là:

A. -1.

B. 2.

C. 1.

D. 3.

Câu 12. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=\frac{2m^{2}x-5}{x+3}$ nhận đường thẳng y=8 làm tiệm cận ngang.

A. $m=2.$

B. $m=-2.$

C. $m=\pm 2.$

D. $m=0$

Câu 13. Biết rằng đồ thị hàm số $y=\frac{\left(m-2n-3\right)x+5}{x-m-n}$ nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng $S=m^2+n^2-2.$

A. $S=2.$

B. $S=0.$

C. $S=-1.$

D. $S=1.$

Câu 14. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=\frac{2x^2-3x+m}{x-m}$ không có tiệm cận đứng.

A. $m=0$

B. $m=1,m=2$

C. $m=0,m=1$

D. $m=1$

Câu 15. Tìm tất cả các giá trị thực của tham số a để đồ thị hàm số $y=\frac{x^2+1}{3x^2-2ax+a}$ có đúng một tiệm cận đứng.

A. $a=\pm \sqrt{\frac{3}{2}}.$

B. $a=0,a=3.$

C. $a=1,a=2.$

D. $a=\pm 2.$

Câu 16. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=\frac{x+2}{x^2-4x+m}$ có đúng một tiệm cận ngang và đúng một tiệm cận đứng.

A. $m<4.$

B. $m>4.$

C. $m=4,m=-12.$

D. $m\ne 4.$

Câu 17. Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn $\left[-2017;2017\right]$ để hàm số $y=\frac{x+2}{\sqrt{x^2-4x+m}}$ có hai tiệm cận đứng.

A. $2018.$

B. $2019.$

C. $2020.$

D. $2021.$

Câu 18. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=\frac{x-3}{x+\sqrt{m{x}^2+4}}$ có đúng một tiệm cận ngang.

A. $m=0,m=1.$

B. $m\ge 0.$

C. $m=1.$

D. $m=0$

Câu 19. Cho hàm số $y=\frac{x-1}{\sqrt{x^2+2(m-1)x+m^2}}$ với m là tham số thực và$m>\frac{1}{2}.$ Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 3

D. 4

Câu 20. Cho hàm số $y=\frac{x-m}{x+1}$ (C) với m là tham số thực. Gọi M là điểm thuộc (C) sao cho tổng khoảng cách từ M đến hai đường tiệm cận của (C) nhỏ nhất. Tìm tất cả các giá trị của để giá trị nhỏ nhất đó bằng 2.

A. $m=0.$

B. $m=2$

C. $m=-2,m=0.$

D. $m=1$

Đáp án