100 bài tập về mặt nón (2024 có đáp án) và cách giải các dạng toán

Mặt nón và phương pháp giải bài tập 

I. Lý thuyết ngắn gọn

1. Định nghĩa mặt nón

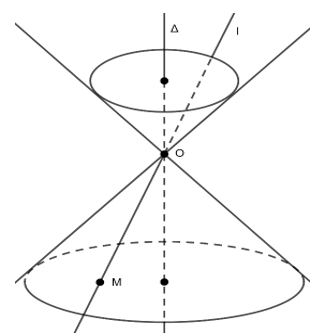
Cho đường thẳng ∆. Xét một đường thẳng l cắt ∆ tại O và không vuông góc với ∆

Mặt tròn xoay sinh bởi đường thẳng l như thế khi quay quanh ∆ gọi là mặt nón tròn xoay (hay mặt nón).

+ ∆ gọi là trục của mặt nón

+ l gọi là đường sinh của mặt nón

+ O gọi là đỉnh của mặt nón

- Nếu gọi $\alpha$ là góc giữa l và ∆ thì $2\alpha$ gọi là góc ở đỉnh của mặt nón $(0°<2\alpha <180°)$

- Nếu M là một điểm tùy ý của mặt nón khác điểm O thì đường thẳng OM nằm hoàn toàn trên mặt nón đó. OM cũng được gọi là đường sinh của mặt nón đó

2. Hình nón và khối nón

- Cho mặt nón (N) với trục ∆, đỉnh O và góc ở đỉnh $2\alpha$. Gọi (P) là mặt phẳng vuông góc với ∆ tại I khác O. Mặt phẳng (P) cắt mặt nón theo đường tròn tâm I. Lại gọi (P’) là mặt phẳng vuông góc với ∆ tại O.

Khi đó, phần của mặt nón (N) giới hạn bởi hai mặt phẳng (P) và (P’) cùng với hình tròn tâm I xác định được gọi là hình nón.

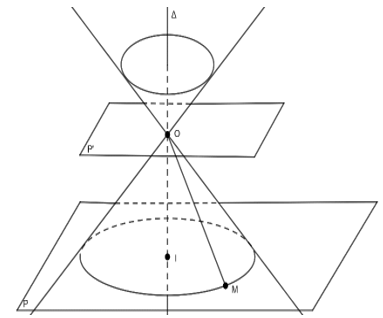
- Khối nón: Một hình nón chia không gian thành hai phần: phần bên trong và phần bên ngoài của nó. Hình nón cùng với phần bên trong của nó gọi là khối nón.

3. Thiết diện khi cắt bởi mặt phẳng

a. Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:

- Mặt phẳng (Q) cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân

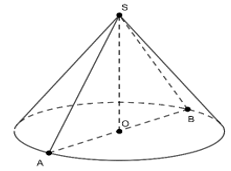
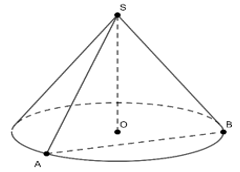
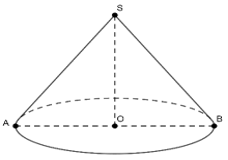
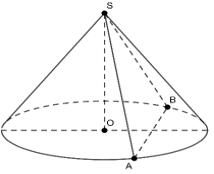
Trên hình vẽ thiết diện là tam giác SAB

- Mặt phẳng (Q) tiếp xúc với mặt nón theo 1 đường sinh thì (Q) là mặt phẳng tiếp diện của hình nón

b. Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:

- Mặt phẳng (Q) vuông góc với trục hình nón thì giao tuyến là 1 đường tròn

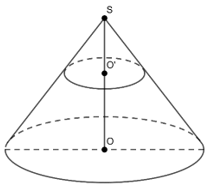
Trên hình vẽ, thiết diện là đường tròn tâm O’

- Mặt phẳng (Q) song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của một hypebol

- Mặt phẳng (Q) song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol

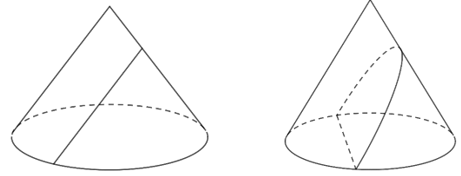
- Mặt phẳng (Q) cắt mọi đường sinh hình nón thì giao tuyến là một đường elip

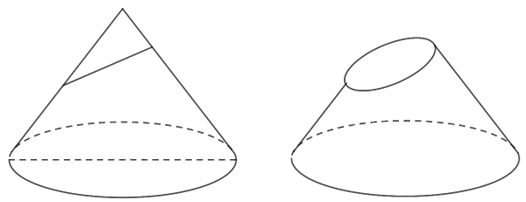
4. Diện tích hình nón và thể tích khối nón.

Một hình chóp gọi là nội tiếp hình nón nếu:

- Đáy của hình chóp là đa giác nội tiếp đáy của hình nón

- Đỉnh của hình chóp là đỉnh của hình nón

a. Định nghĩa.

Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của một hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.

Thể tích của khối nón là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh tăng lên vô hạn.

b. Diện tích xung quanh, diện tích toàn phần của hình nón.

Hình nón có chiều cao là h, bán kính đáy r và độ dài đường sinh là l

- Diện tích xung quanh: $S_{xq}=\pi rl$

- Diện tích đáy: $S_d=\pi r^2$

- Diện tích toàn phần:

$S_{tp}=S_{xq}+S_d=\pi rl+\pi r^2$

c. Thể tích của khối nón:

- Thể tích của khối nón có bán kính r và chiều cao h là:

$V=\frac{1}{3}{S}_d.h=\frac{1}{3}\pi r^{2}h$

d. Mối liên hệ giữa chiều cao, đường sinh và bán kính đáy

Tam giác SAO vuông tại A, có $S{A}^2=S{O}^2+O{A}^2$

Do đó: $l^2=h^2+R^2$ (tham khảo hình vẽ dưới)

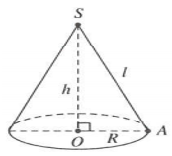
II. Các dạng bài tập

Dạng 1: Tính diện tích xung quanh, diện tích toàn phần, thể tích

Phương pháp giải: Sử dụng công thức:

Diện tích xung quanh hình nón: $S_{xq}=\pi rl$

Diện tích toàn phần hình nón: $S_{tp}=\pi rl+\pi r^2$

Thể tích khối nón: $V=\frac{1}{3}{S}_d.h=\frac{1}{3}\pi r^{2}h$

Trong đó: h là chiều cao, r là bán kính đáy và l độ dài đường sinh của hình nón.

Ví dụ minh họa

Ví dụ 1: Tính diện tích xung quanh của hình nón có thiết diện qua trục là tam giác vuông cân có diện tích bằng 2?

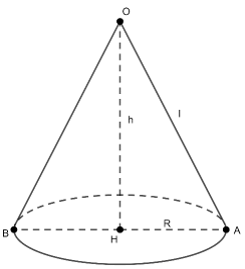
Lời giải

Tam giác OAB vuông cân có diện tích bằng 2

$\Rightarrow \frac{1}{2}O{A}^2=2\Rightarrow OA=2$

Khi đó: $A{B}^2=2O{A}^2={2.2}^2=8$(định lý Py – ta – go)

$$\begin{gathered} \Rightarrow AB=2\sqrt{2} \\ \Rightarrow h=R=\frac{AB}{2}=\sqrt{2} \end{gathered}$$

Vậy diện tích xung quanh của hình nón là:

$S_{xq}=\pi Rl=\pi .R.OA=2\sqrt{2}\pi$

Ví dụ 2: Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng (SAB) bằng $\frac{a\sqrt{3}}{3}$ và $\widehat{SAO}=30°,\widehat{SAB}=60°$. Độ dài đường sinh của hình nón theo a bằng?

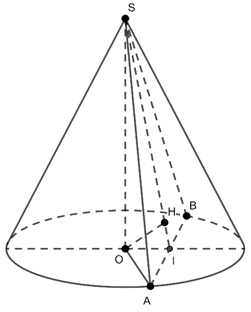
Lời giải

Gọi I là trung điểm của AB. Dựng OH vuông góc SI

Ta có: $OH=\frac{a\sqrt{3}}{3}$

Do $\widehat{SAB}=60°$ nên tam giác SAB đều

Suy ra: SA = SB = AB

Ví dụ 3: Cho tam giác ABC có $\widehat{ABC}=45°,\widehat{ACB}=30°,AB=\frac{\sqrt{2}}{2}$. Quay tam giác ABC xung quanh cạnh BC ta được khối tròn quay có thể tích V bằng bao nhiêu?

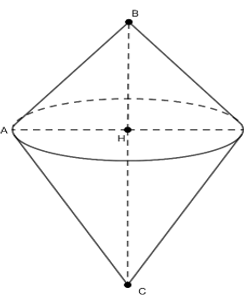
Lời giải

Áp dụng định lý sin trong tam giác ABC, ta có:

Dạng 2: Tương giao giữa nón và mặt phẳng, bài toán thiết diện

Phương pháp giải:

a. Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:

- Mặt phẳng (Q) cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân

- Mặt phẳng (Q) tiếp xúc với mặt nón theo 1 đường sinh thì (Q) là mặt phẳng tiếp diện của hình nón

b. Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:

- Mặt phẳng (Q) vuông góc với trục hình nón thì giao tuyến là 1 đường tròn

- Mặt phẳng (Q) song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của một hypebol

- Mặt phẳng (Q) song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol

- Mặt phẳng (Q) cắt mọi đường sinh hình nón thì giao tuyến là một đường elip

Ví dụ minh họa

Ví dụ 1: Cho hình nón có thiết diện qua đỉnh S tạo với đáy góc 60 độ là tam giác đều cạnh bằng 4 cm. Tính thể tích khối nón đó.

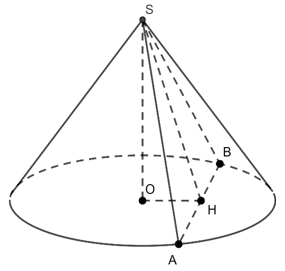
Lời giải

Gọi H là trung điểm AB

Gọi thiết diện qua đỉnh là tam giác SAB, tâm đường tròn đáy là O

Ta tìm góc giữa (SAB) và đáy

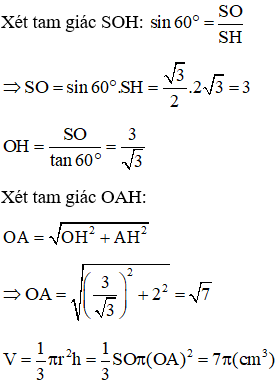
Ví dụ 2: Cho khối nón tròn xoay có đường cao h = a và bán kính đáy $r=\frac{5a}{4}$. Một mặt phẳng (P) đi qua đỉnh của khối nón và có khoảng cách đến tâm O của đáy bằng $\frac{3a}{5}$. Diện tích thiết diện tạo bởi (P) và hình nón là bao nhiêu?

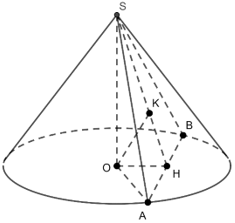
Lời giải

Gọi mặt phẳng qua đỉnh là tam giác SAB

Khoảng cách từ O đến mặt phẳng (SAB)

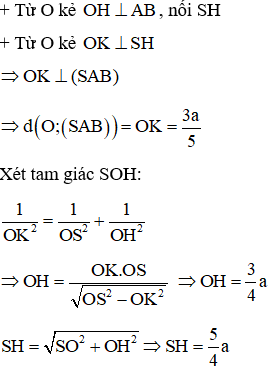
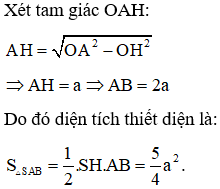
Dạng 3: Sự tạo thành nón

Phương pháp giải: Sử dụng định nghĩa mặt nón, hình nón, khối nón và các công thức liên quan.

Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, $SC=a\sqrt{6}$. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Tính thể tích của khối nón tròn xoay đó?

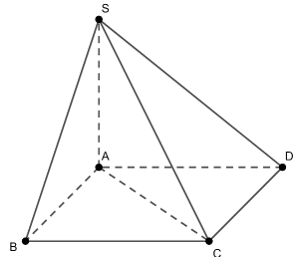
Lời giải

Xét tam giác ABC vuông tại B

$$\begin{gathered} AC=\sqrt{A{B}^2+B{C}^2} \\ \Rightarrow AC=a\sqrt{2} \\ SA=\sqrt{S{C}^2-A{C}^2} \\ \Rightarrow SA=2a \end{gathered}$$

Hình nón tròn xoay được tạo thành là một hình nón có thể tích là:

$$\begin{gathered} V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi A{C}^2.SA \\ \Rightarrow V=\frac{4\pi a^3}{3} \end{gathered}$$

Ví dụ 2: Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh hình nón đó

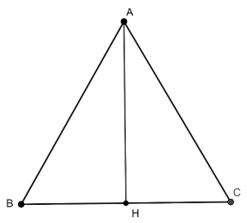
Lời giải

Tam giác ABC đều, đường cao AH

$\Rightarrow BH=\frac{a}{2}$

Hình nón tròn xoay được tạo thành là một hình nón có $r=\frac{a}{2};l=a$

$S_{xq}=\pi rl=\frac{\pi a^2}{2}$

Dạng 4: Bài toán cực trị

Phương pháp giải:

- Áp dụng các công thức liên quan, đưa bài toán hình học về bài toán đại số (đại số hóa hình học).

- Khảo sát hàm số f(x) trên khoảng xác định (đạo hàm – lập bảng biến thiên)

Ví dụ minh họa

Ví dụ 1: Khi cắt hình nón có chiều cao 16 cm và đường kính đáy 24 cm bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất là bao nhiêu?

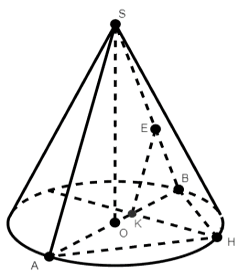
Lời giải

Cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện là một parabol

Xét dây cung bất kỳ chứa đoạn KH như hình vẽ

Suy ra tồn tại đường kính $AB\perp KH$

Trong tam giác SAB, KE // SA, E thuộc SB

Suy ra parabol nhận KE làm trục như hình vẽ chính là một thiết diện thỏa mãn yêu cầu bài toán (thiết diện này song song với đường sinh SA)

Đặt BK = x (0 < x < 24)

Trong tam giác ABH có:

$H{K}^2=BK.AK=x(24-x)$

Trong tam giác SAB có:

$\frac{KE}{SA}=\frac{BK}{BA}$

Thiết diện thu được là một parabol có diện tích:

$$\begin{gathered} S=\frac{4}{3}KH.KE \\ \iff KE=\frac{BK}{BA}.SA \\ \iff KE=\frac{5x}{6} \end{gathered}$$

Ta có:

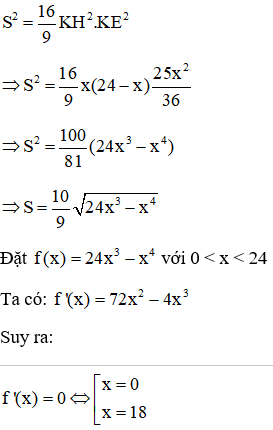
Bảng biến thiên:

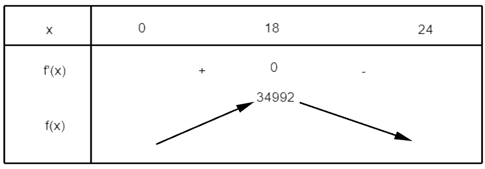
Vậy thiết diện có diện tích lớn nhất là

$$\begin{gathered} S=\frac{10}{9}\sqrt{24x^3-x^4} \\ =\frac{10}{9}.\sqrt{34992} \end{gathered}$$

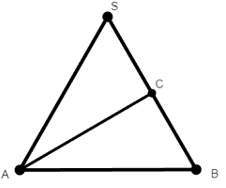
Ví dụ 2: Tại trung tâm thành phố người ta tạo điểm nhấn bằng cột trang trí hình nón có kích thước: chiều dài đường sinh l = 10m, bán kính đáy R = 5m. Biết tam giác SAB là thiết diện qua trục của hình nón và C là trung điểm SB. Trang trí hệ thống đèn điện tử chạy từ A đến C trên mặt nón. Xác định giá trị ngắn nhất của chiều dài dây đèn điện tử?

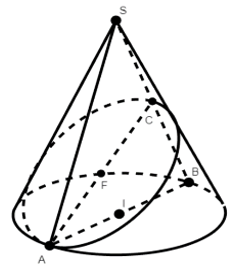
Lời giải

Ta có tam giác SAB cân và SB = AB

Suy ra tam giác SAB đều

Diện tích xung quanh hình nón là:

$S_{xq}=\pi Rl=50\pi \left(m^2\right)$

Vẽ (P) đi qua C và vuông góc với AB. Mặt phẳng (P) cắt hình nón theo thiết diện là một Elip

Khi đó chiều dài dây đèn điện ngắn nhất chính là chiều dài dây cung AC trên Elip

Ta dung phương pháp trải hình ra sẽ thấy ngay như sau:

Hình trải dài là một hình quạt với AB là độ dài nửa đường tròn và:

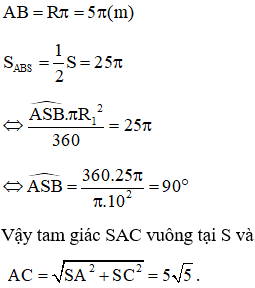
III. Bài tập áp dụng

Bài 1: Giao của mặt phẳng đi qua trục của hình nón, cắt đường tròn đáy của hình nón tại hai điểm là hình gì?

A. Hình tròn

B. Hình vuông

C. Hình tam giác

D. Hình bình hành

Bài 2: Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh huyền 2a. Thể tích của khối nón bằng:

A. $\pi a^3$

B. $2\pi a^3$

C. $\frac{2\pi a^3}{3}$

D. $\frac{\pi a^3}{3}$

Bài 3: Một hình nón có bán kính đường tròn đáy bằng a. Thiết diện qua trục của hình nón là một tam giác có góc ở đỉnh bằng $120°$. Gọi V là thể tích khối nón. Khi đó V bằng:

A. $\frac{\pi a^3}{6}$

B. $\frac{\pi a^3\sqrt{3}}{3}$

C. $\frac{\pi a^3\sqrt{3}}{9}$

D. $\frac{\pi a^3}{3}$

Bài 4: Trong các hình nón cùng có diện tích toàn phần bằng S. Hình nón có thể tích lớn nhất khi ( r, l lần lượt là bán kính đáy và đường sinh của hình nón).

A. $l=3r$

B. $l=2\sqrt{2}r$

C. $l=r$

D. $l=2r$

Bài 5: Xét các hình nón có đường sinh với độ dài đều bằng 10 cm. Chiều cao của hình nón có thể tích lớn nhất là:

A. $5\sqrt{3}cm$

B. $10\sqrt{3}cm$

C. $\frac{5\sqrt{3}}{3}cm$

D. $\frac{10\sqrt{3}}{3}cm$

Bài 6: Giả sử đồ thị hàm số $y=(m+1)x^4-2m{x}^2+m^2+1$ có 3 điểm cực trị là A, B, C mà $x_A<x_B<x_C$. Khi quay tam giác ABC quanh cạnh AC ta được khối tròn xoay. Giá trị của m để thể tích của khối tròn xoay đó lớn nhất thuộc khoảng nào?

A. (4; 6)

B. (2; 4)

C. (-2; 0)

D. (0; 2)

Bài 7: Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng $\sqrt{3}$ và thiết diện qua trục là tam giác đều là:

A. $8\pi$

B. $9\pi$

C. $10\pi$

D. $1\pi$

Bài 8: Một khối nón có thể tích bằng V, nếu giữ nguyên chiều cao và tang bán kính khối nón lên 2 lần thì thể tích mới bằng

A. 2V

B. 4V

C. 3V

D. 6V

Bài 9: Diện tích xung quanh của một hình nón có bán kính đáy bằng 3 và chiều cao bằng 4 là:

A. $15\pi$

B. $30\pi$

C. $36\pi$

D. $12\pi$

Bài 10: Tính độ dài đường sinh của hình nón có diện tích xung quanh $25\pi$, bán kính đường tròn đáy bằng 5.

A. 5

B. 1

C. 3

D. 2,5